In recent years, the adoption of renewable energy sources has gained significant momentum, with solar power standing out as a key contributor to sustainable development. Among various applications, the off-grid solar system has emerged as a critical solution for providing electricity in remote locations or as a backup power source. This type of system operates independently of the main utility grid, offering advantages such as energy independence and enhanced reliability during grid outages. However, integrating photovoltaic (PV) sources into an off-grid solar system introduces challenges related to stability, as PV inverters act as zero-inertia distributed generators. These challenges include fluctuations in voltage, current, and power flow, which can impact the overall performance of the system. In this article, I explore the steady-state behavior of an off-grid solar system using ETAP simulation software, focusing on how variations in PV capacity affect system stability through power flow and short-circuit analysis.
The off-grid solar system under consideration comprises several key components: PV arrays, inverters, distribution boards, loads, and protection devices. This setup ensures that the system can function autonomously, supplying power to critical loads without reliance on external grids. A typical off-grid solar system is designed to handle both normal and emergency operating conditions. For instance, under normal circumstances, the main generation units power all connected loads, while during emergencies—such as generator failures—the system switches to backup sources like emergency generators or battery storage. The heart of this system lies in the coordination between the PV sources and the distribution infrastructure, which must maintain voltage and frequency within acceptable limits to prevent instability. To model this, I utilized ETAP, a powerful power system simulation tool, to create a single-line diagram that captures the intricate interactions within the off-grid solar system. This approach allows for a detailed analysis of steady-state parameters, such as power losses and voltage drops, under varying levels of PV penetration.
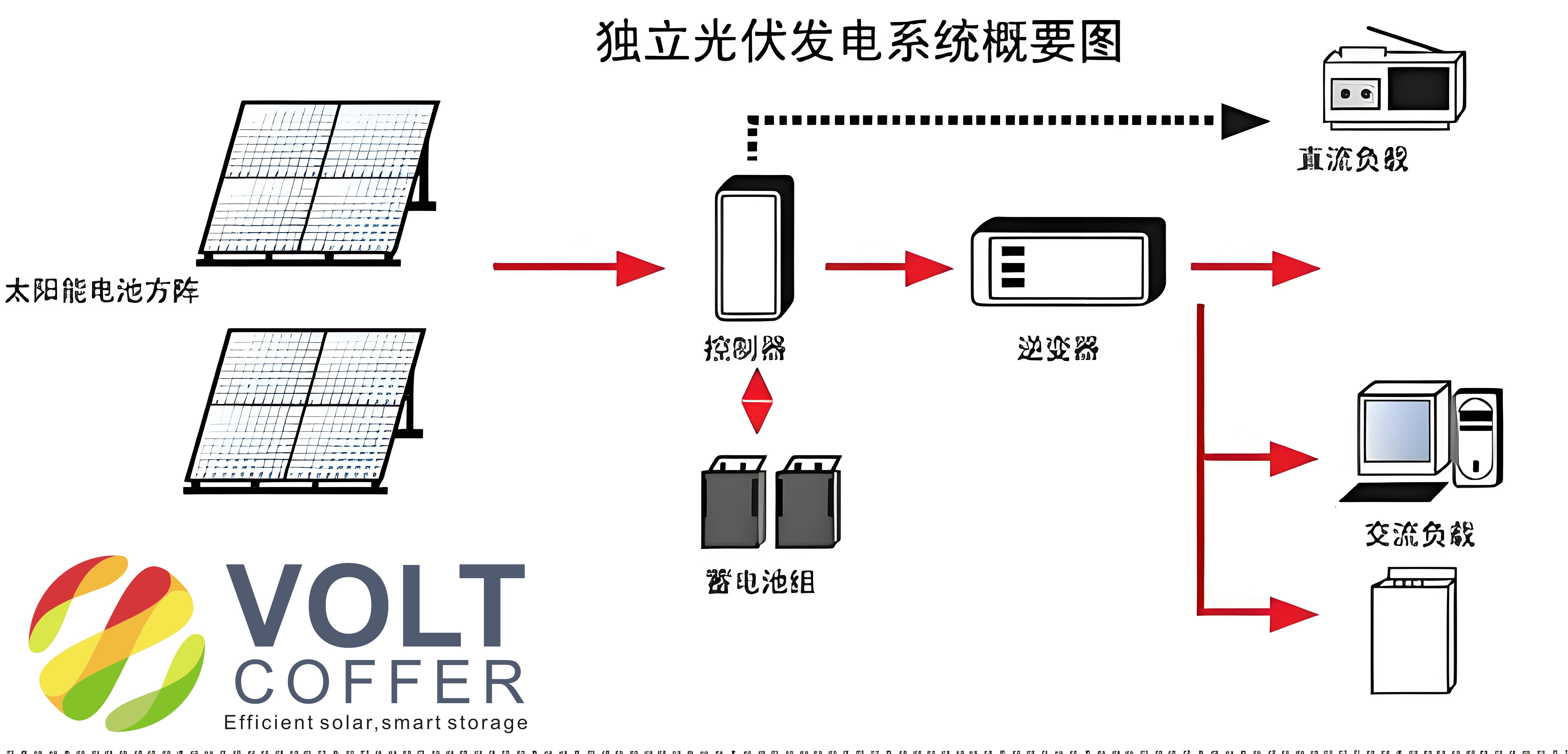
In the system described, the PV arrays are configured using monocrystalline silicon panels, specifically the YL255P-32b model, which has a peak power rating of 255W under standard test conditions. For this off-grid solar system, I arranged 20 solar cells in series to form a string, with 30 such strings connected in parallel to create a single PV panel. This results in a total of 600 cells per panel, optimized for efficient energy harvesting. The performance characteristics of these panels, such as current-voltage (I-V) and power-voltage (P-V) curves, are crucial for understanding how the off-grid solar system responds to changes in solar irradiance. For example, under constant temperature and varying irradiance, the I-V curve shows a linear increase in current with higher irradiance, while the P-V curve demonstrates a peak power point that shifts with environmental conditions. These characteristics influence the overall efficiency of the off-grid solar system, as they determine the maximum power extraction and integration into the distribution network.
To assess the steady-state performance of the off-grid solar system, I conducted power flow analysis using ETAP. Power flow calculations are essential for determining the distribution of active and reactive power, voltage magnitudes, and phase angles across the system. Common methods for power flow analysis include the Gauss-Seidel method, fast decoupled method, and Newton-Raphson method. In this study, I employed the Newton-Raphson method due to its robustness and rapid convergence for nonlinear systems. The general power flow equations for a bus in the off-grid solar system can be expressed as:
$$P_i = V_i \sum_{j=1}^{N} V_j (G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij})$$
$$Q_i = V_i \sum_{j=1}^{N} V_j (G_{ij} \sin \theta_{ij} – B_{ij} \cos \theta_{ij})$$
where \(P_i\) and \(Q_i\) are the active and reactive power injections at bus \(i\), \(V_i\) and \(V_j\) are the voltage magnitudes at buses \(i\) and \(j\), \(G_{ij}\) and \(B_{ij}\) are the conductance and susceptance of the line between buses \(i\) and \(j\), and \(\theta_{ij}\) is the phase angle difference. For the off-grid solar system, the PV sources are typically modeled as PQ nodes, where active power injection is fixed based on solar input, and reactive power is controlled to maintain voltage stability. By simulating different scenarios with varying PV capacities, I analyzed how the off-grid solar system’s power flow changes, particularly focusing on parameters like line losses and voltage profiles.
One key metric in this analysis is the PV penetration rate, defined as the ratio of the installed PV capacity to the total load demand in the off-grid solar system. This rate directly impacts system stability; for instance, higher penetration can lead to reduced reliance on conventional generators but may also cause voltage fluctuations if not properly managed. In this off-grid solar system, the PV penetration was limited to a maximum of 23% to ensure stability, as per design guidelines. To investigate this, I varied the PV capacity from 0 kW to 210 kW in increments, while keeping the connection point fixed at the main distribution board. The results from the power flow analysis are summarized in the following tables, which illustrate the impact on line losses and voltage drops across different components of the off-grid solar system.
| PV Capacity (kW) | Total Line Losses (kW) | Line Losses Excluding PV (kW) |
|---|---|---|
| 0 | 25.84 | 25.84 |
| 30 | 25.297 | 25.28 |
| 60 | 24.826 | 24.759 |
| 90 | 24.4 | 24.249 |
| 120 | 24.018 | 23.75 |
| 150 | 23.667 | 23.249 |
| 180 | 23.402 | 22.801 |
| 210 | 23.167 | 22.35 |
As shown in the table, increasing the PV capacity in the off-grid solar system leads to a consistent reduction in total line losses. For example, at 0 kW PV capacity, the total losses are 25.84 kW, which decrease to 23.167 kW at 210 kW PV capacity. This trend indicates that the integration of PV sources improves the efficiency of the off-grid solar system by reducing energy dissipation in the conductors. The losses excluding PV also follow a similar pattern, highlighting that the PV integration not only supplements power but also optimizes the overall power flow distribution. This is particularly beneficial for an off-grid solar system, where minimizing losses is crucial for maximizing the available energy for loads.
In addition to power flow analysis, I performed short-circuit calculations to evaluate the transient behavior of the off-grid solar system during fault conditions. Short-circuit analysis helps in determining the maximum current that flows through the system when a fault occurs, which is vital for selecting appropriate protection devices. The impedance method is commonly used for such calculations, where the short-circuit current \(I_{sc}\) is given by:
$$I_{sc} = \frac{V}{Z_{eq}}$$
where \(V\) is the pre-fault voltage and \(Z_{eq}\) is the equivalent impedance at the fault point. For the off-grid solar system, this involves modeling the contributions from both synchronous generators and PV inverters. The results from the short-circuit analysis revealed that as PV penetration increases, the fault current levels change due to the altered impedance paths. However, in this off-grid solar system, the voltage stability remained within acceptable limits, as evidenced by the steady voltage profiles observed during simulations.
To further illustrate the impact of PV capacity on voltage stability, I analyzed the voltage drops across various branches in the off-grid solar system. The following table provides data on voltage drops at key points, such as PV branches, generator outputs, and critical cables, under different PV capacities.
| PV Capacity (kW) | PV Branch Drop (kV) | Generator 1 Drop (kV) | Generator 2 Drop (kV) | Generator 3 Drop (kV) | Cable5 Drop (kV) | Cable6 Drop (kV) | Cable12 Drop (kV) | Cable13 Drop (kV) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.146 | 2.71 | 2.7 | 2.7 | 0.647 | 0.647 | 0.755 | 0.755 |
| 30 | 0.146 | 2.71 | 2.7 | 2.7 | 0.647 | 0.647 | 0.755 | 0.755 |
| 60 | 0.292 | 2.71 | 2.7 | 2.7 | 0.649 | 0.647 | 0.757 | 0.753 |
| 90 | 0.438 | 2.61 | 2.6 | 2.7 | 0.652 | 0.643 | 0.76 | 0.75 |
| 120 | 0.583 | 2.51 | 2.5 | 2.7 | 0.655 | 0.64 | 0.763 | 0.746 |
| 150 | 0.728 | 2.41 | 2.4 | 2.7 | 0.657 | 0.637 | 0.767 | 0.743 |
| 180 | 0.873 | 2.41 | 2.4 | 2.7 | 0.66 | 0.634 | 0.77 | 0.739 |
| 210 | 1 | 2.31 | 2.3 | 2.7 | 0.663 | 0.631 | 0.774 | 0.736 |
From the data, it is evident that as the PV capacity in the off-grid solar system increases, the voltage drop across the PV branch rises linearly, from 0.146 kV at 0 kW to 1 kV at 210 kW. This is expected because higher PV output leads to greater current flow through the PV circuit. Conversely, the voltage drops associated with synchronous generators (Generator 1 and Generator 2) decrease significantly with higher PV penetration. For instance, at 0 kW PV, Generator 1 has a drop of 2.71 kV, which reduces to 2.31 kV at 210 kW. This reduction indicates that the PV sources are sharing the load burden, thereby reducing the power output required from the generators and improving voltage stability in those branches. The cable voltage drops show minor variations, but overall, the system maintains stable voltage levels, demonstrating the resilience of this off-grid solar system under changing conditions.
The relationship between PV penetration and system performance can be further explained using mathematical models. For instance, the overall efficiency \(\eta\) of the off-grid solar system can be expressed as a function of PV capacity \(P_{pv}\) and total load \(P_{load}\):
$$\eta = \frac{P_{load} – P_{loss}}{P_{pv} + P_{gen}}$$
where \(P_{loss}\) represents the total power losses, and \(P_{gen}\) is the power from conventional generators. As \(P_{pv}\) increases, \(P_{gen}\) decreases, leading to improved efficiency as long as losses are minimized. Additionally, the voltage stability index \(VSI\) for a bus in the off-grid solar system can be defined as:
$$VSI = V_i – \sum_{j \neq i} Z_{ij} I_j$$
where \(V_i\) is the voltage at bus \(i\), \(Z_{ij}\) is the impedance between buses, and \(I_j\) is the current injection. Simulations showed that with higher PV penetration, the VSI values improved, indicating enhanced voltage regulation in the off-grid solar system.
In conclusion, the steady-state analysis of this off-grid solar system using ETAP reveals several important insights. First, the integration of PV sources reduces line losses and improves overall system efficiency, making the off-grid solar system more sustainable. Second, while increasing PV capacity leads to higher voltage drops in PV branches, it alleviates the burden on conventional generators, resulting in lower voltage drops in those areas and better voltage stability. The off-grid solar system demonstrates robustness up to a PV penetration rate of 23%, beyond which stability issues might arise. This study underscores the importance of using advanced simulation tools like ETAP for designing and optimizing off-grid solar systems, as they provide accurate, system-level insights that are closer to real-world conditions compared to traditional methods. Future work could explore dynamic stability analysis or the integration of energy storage to further enhance the performance of off-grid solar systems in varying environmental scenarios.
