Energy storage has become an indispensable part of the power system, and distributed battery energy storage systems have significant advantages in energy density and have been widely deployed in power systems. At present, research on the control of battery energy storage systems mostly focuses on separating their optimization control and battery state of charge (SOC) equalization. For the control of battery energy storage systems: utilizing the principle of empirical mode decomposition to achieve optimal power allocation; Using the genetic simulated annealing algorithm, the objective function is to minimize the power exceeding the limit of battery energy storage charging and discharging, achieving power allocation while avoiding the state of charge exceeding the limit; Propose a variable adjustment factor SOC droop control strategy to improve power response speed by changing the adjustment factor; Utilize an improved alternating direction multiplier algorithm to achieve battery energy storage equipment management and distribution network voltage support. The above control strategies only consider power allocation and avoid SOC exceeding limits, without considering the issue of reducing battery capacity utilization and shortening battery life caused by SOC imbalance.
For SOC balancing technology, there are currently two main types: energy dissipation and energy transfer. The former consumes excess electricity through resistors, which can cause waste of electricity; The latter achieves energy transfer through inductance and capacitance, which to some extent increases the charging and discharging frequency of the battery and accelerates its aging. In response to these issues, by improving the droop control and adding the average SOC of the battery to the droop coefficient, the SOC of each battery unit can be balanced, but it will cause the droop coefficient to be too large, resulting in significant bus voltage deviation. The proposed balancing strategy can achieve high-precision SOC balancing for each battery energy storage unit, but using centralized control methods poses significant communication pressure.
Therefore, this article proposes a distributed battery energy storage system collaborative control strategy based on SOC balancing, which eliminates the need for additional balancing circuits and enables each battery unit to achieve SOC dynamic balancing while suppressing power fluctuations in the grid. Combined with the battery charging and discharging grouping strategy, the frequency of battery charging and discharging is reduced, thereby extending battery life. This control strategy is based on a distributed communication network. Compared to centralized control, the control center bears less communication pressure and can also enable collaborative cooperation among distributed battery energy storage units, effectively improving battery utilization.
1. SOC packet balancing strategy based on MAS
To achieve collaborative control of distributed battery energy storage systems and achieve SOC balancing among battery energy storage units, a SOC group balancing strategy based on multi-agent system (MAS) is proposed. Taking the 33 node microgrid as an example, the topology of its battery energy storage system is shown in Figure 1. A total of 10 battery units are installed at the DG1~DG4 distributed power sources to form the distributed battery energy storage system. The solid line represents the physical connection, and the dashed line represents the communication connection. These 10 distributed battery cells form a MAS, and each battery cell is one of the agents. Each agent only has communication connections with neighboring agents.
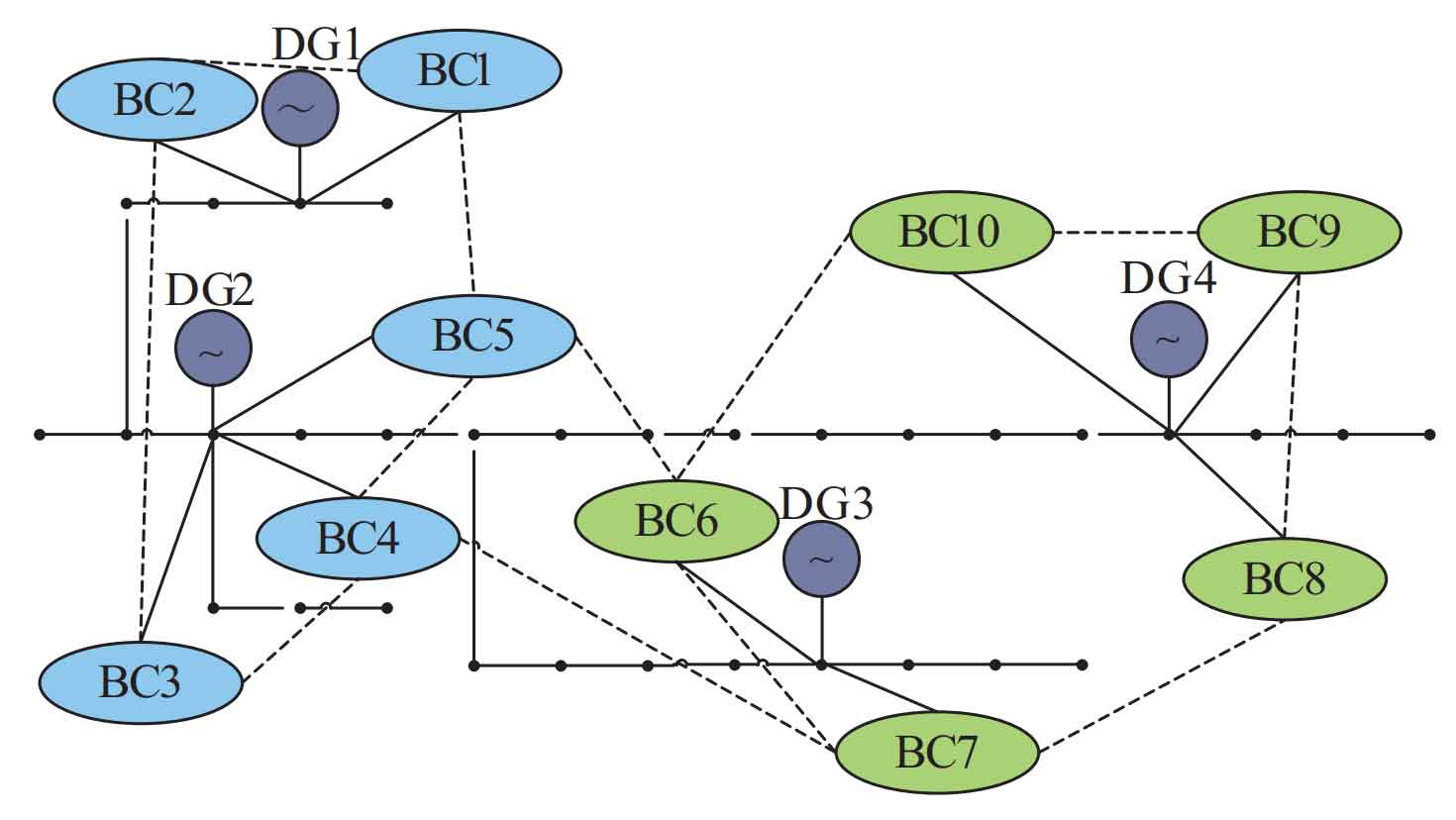
In the actual control process, in order to suppress power fluctuations in the power grid, the battery energy storage system needs to frequently switch between charging and discharging states, which to some extent increases the charging and discharging frequency of the battery and accelerates its aging. At the same time, the capacity of each battery energy storage unit is not fully utilized. Based on the above considerations, on the basis of the balancing strategy mentioned above, the battery cells in the battery energy storage system are divided into two subsystems, which respectively perform charging/discharging tasks to reduce unnecessary switching of charging/discharging states and thus reduce the charging and discharging frequency of the battery. It should be noted that at certain times, there may be situations where the power command is greater than the rated power of a single subsystem. In this case, another subsystem needs to cooperate and provide short-term power support to digest the power command together.
2. Multi agent distributed algorithm
In order to implement the SOC balancing strategy mentioned in the previous section, this section proposes a multi-agent distributed algorithm based on model based predictive control (MPC), which achieves fast and adaptive allocation of total power instruction Pb among various agents. The convergence speed is faster than traditional multi-agent algorithms and can meet the requirements of real-time control.
Provide a brief introduction to the graph theory analysis method for multi-agent networks. Use a graph G (V, E) to represent the network topology of MAS, where V is the vertex set representing each agent, and E is the edge set representing the communication connections between agents. If there is a path from each agent to any other agent, then G is called a connected graph. For connected graph G, there are three important matrix definitions mentioned in this article.
1) Adjacency matrix A
The adjacency matrix A is a square matrix with zero main diagonal elements and a number of nodes in order. Specifically, it can be expressed as:

2) Degree matrix D
The degree matrix D has the same order as the adjacency matrix A, which is a symmetric matrix with zero elements except for the main diagonal. Specifically, it can be expressed as:
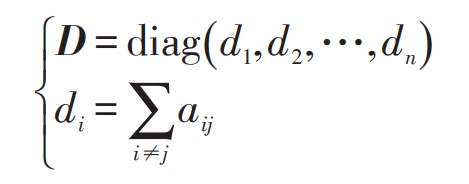
3) Laplace matrix L
The Laplace matrix of multi-agent is:
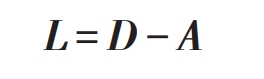
2.1 Traditional multi-agent distributed algorithms
There are various forms of traditional consistency algorithms based on MAS, among which the matrix form of the discrete time weighted consistency algorithm is:
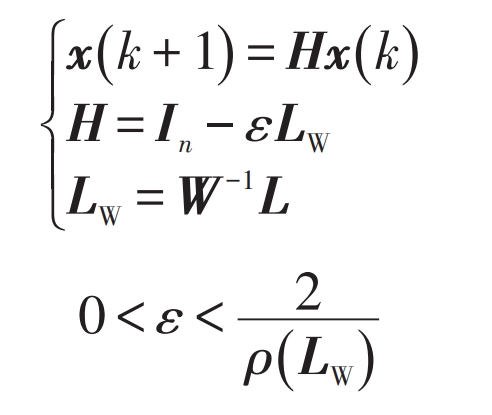
In the formula: x – consistency variable; In – n-th order identity matrix; ε —— Iteration step size; W – Weighted matrix, W=diag (w1, w2,…, wn); ρ (LW) – Spectral radius of matrix LW.
The algorithm principle of the formula is to reduce the state difference between adjacent agents as the goal, so that the state variable x gradually approaches the weighted average of the initial value x (0). In the control strategy proposed in this article, power is used as the state variable, and the above algorithm combined with the output equation can achieve adaptive allocation of power instructions in each battery cell. The specific mathematical model is:
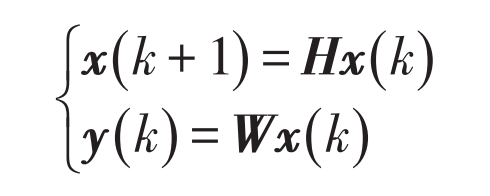
2.2 Multi Agent Distributed Algorithm Based on MPC
Although the algorithm shown in the formula can achieve the control strategy mentioned in Section 1, it requires too many iterations to achieve reasonable accuracy and cannot meet the requirements of real-time control. Therefore, this section proposes a multi-agent distributed algorithm based on MPC. Introduce the virtual control variable u to obtain the state space equation:
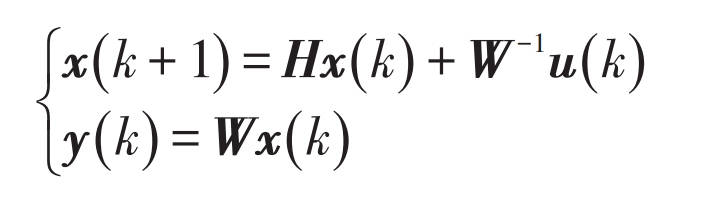
The key to this algorithm is to control the generation of variable u. The characteristic of model predictive control is that it can predict the future state of the system based on its current state. If the current time is k, the predicted state is:
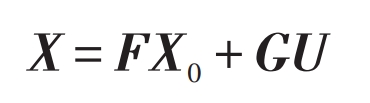

In the formula: Nc – control time domain; Np – prediction time domain.
Predict the future output of the system based on the formula:
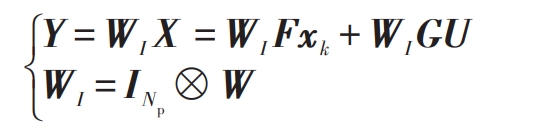
In the formula: INp – Np order identity matrix; ⊗—— Kronecker product.
The cost function is to minimize the error between the predicted output and the output reference quantity:
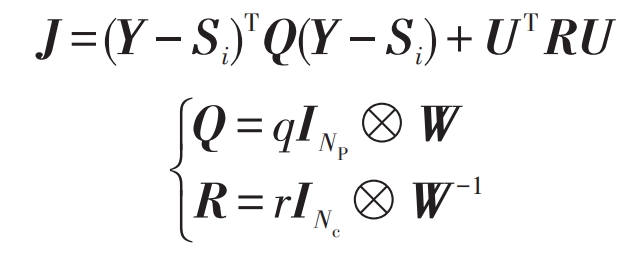
In the formula: Si – output reference quantity; Q>0, r>0; Q – State weight matrix; R – Control input weight matrix.
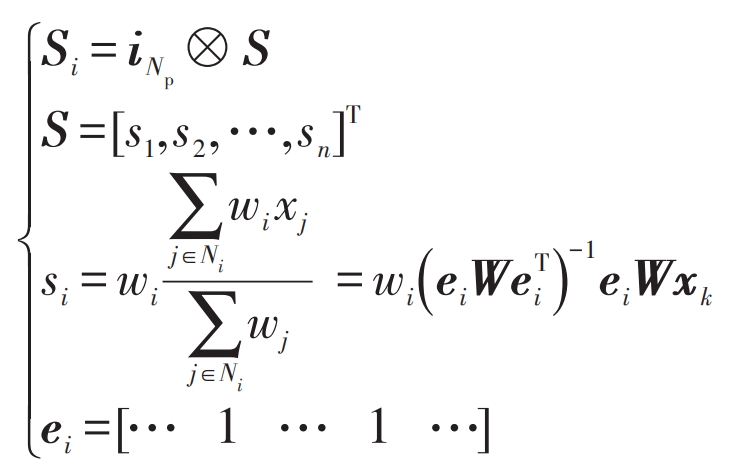
In the formula: iNp – Np order column vector with all elements being 1; Ni – the set composed of intelligent agent i and its neighboring intelligent agents; The elements belonging to Ni in ei are all 1, while the other elements are all 0.
Organize the formulas and obtain:
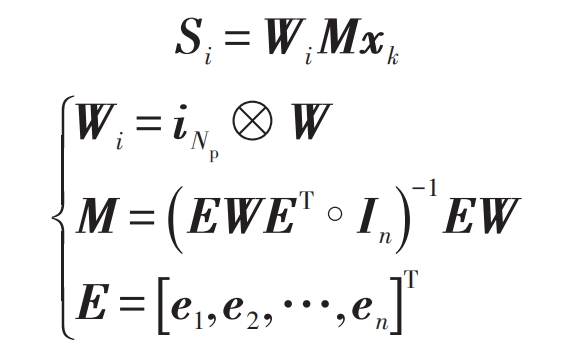
In the formula: In – n-th order identity matrix—— Hadamard product.
Substituting the formula into can obtain:
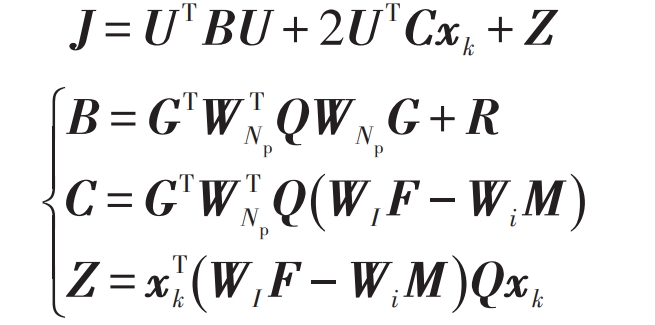
By taking the partial derivative of U from the formula and making it equal to 0, the optimal solution for the control variable U can be obtained:
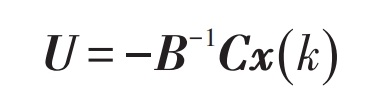
Then take the first element u (k) of the column vector U as the actual input control variable of the formula:
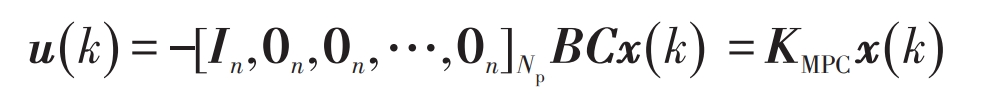
KMPC is the state feedback gain matrix of multi-agent systems. Finally, by substituting the formula, the state equation of the final closed-loop control form can be obtained:
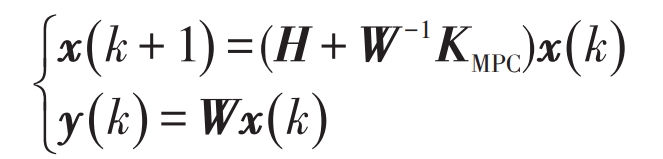
All the above deductions only use information between adjacent agents, which is a completely distributed process. Compared to traditional multi-agent algorithms that only consider the current state information of the system, multi-agent distributed algorithms based on MPC also take into account the difference information of the system’s future state and output, resulting in faster convergence speed. Within each control cycle, the initial value x0 is:
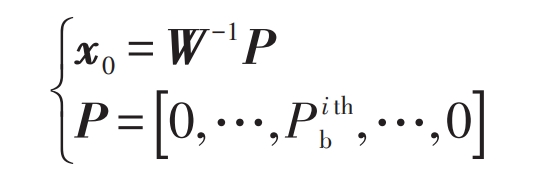
In the formula: Pi thb – The i-th intelligent agent receives the total power instruction Pb, and the intelligent agent receiving the power instruction can be arbitrarily selected.
2.3 Implementation of Algorithm
The key to using the algorithm proposed in section 2.2 to achieve the SOC equilibrium strategy proposed in section 1 is the generation of adjacency matrix A and weighting matrix W. For a multi-agent system composed of n battery cells, the adjacency matrix A is:
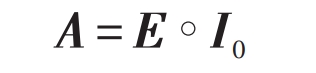
In the formula: E – nth order square matrix; I0- An n-order square matrix with all diagonal elements being 0 and all other elements being 1.
The generation of matrix W is related to the current charging/discharging state of the battery cell. Define its diagonal elements as:
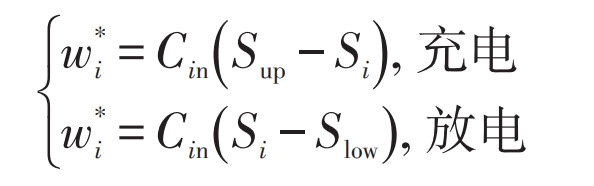
In the formula: Cin – rated capacity of battery unit i; Sup – Upper limit value of state of charge; Si – Current state of charge of battery unit i; Low – Lower limit value of state of charge.
According to the formula definition, the weight w * i is determined by the current remaining capacity or remaining power of each battery unit, which meets the requirements of the SOC balancing strategy mentioned above. It is worth noting that if the rated capacity of the battery cell is large and Si is low (charging) or high (discharging), it will result in a larger calculated weight value, which will reduce the convergence speed of the algorithm. Therefore, a formula is used to reduce the weight value.
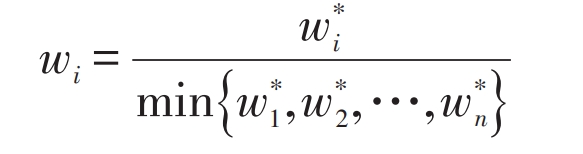
By combining the generation method of adjacency matrix A and weighting matrix W with the algorithm in section 2.2, the control strategy proposed in section 1 can be achieved.
3. Example analysis
In order to verify the effectiveness and advantages of the strategies proposed in Section 1 and the algorithms proposed in Section 2, this section uses Matlab software to conduct simulation analysis and explanation from three aspects: SOC equalization effect, battery life analysis, and algorithm convergence speed.
3.1 SOC equalization effect
The specific control process of the SOC equilibrium strategy described in Section 1. Taking the battery energy storage power data of a microgrid in a northwest factory area as an example, the sampling interval is 1 minute, the control time domain Nc=7, and the prediction time domain Np=10, ε = 0.1. The relevant parameters and initial SOC of the battery energy storage system are shown in Table 1.
| Project | Parameter |
| Number of units | 10 |
| Total (unit) capacity/MWh | 20(2) |
| Total (unit) power/MW | 5(0.5) |
| Charging/discharging efficiency/% | 90 |
| SOC Up/SOC Down | 0.9/0.1 |
| Charging system (1-5) initial SOC | 0.4/0.35/0.3/0.2/0.15 |
| Charging system (6-10) initial SOC | 0.85/0.8/0.7/0.65/0.6 |
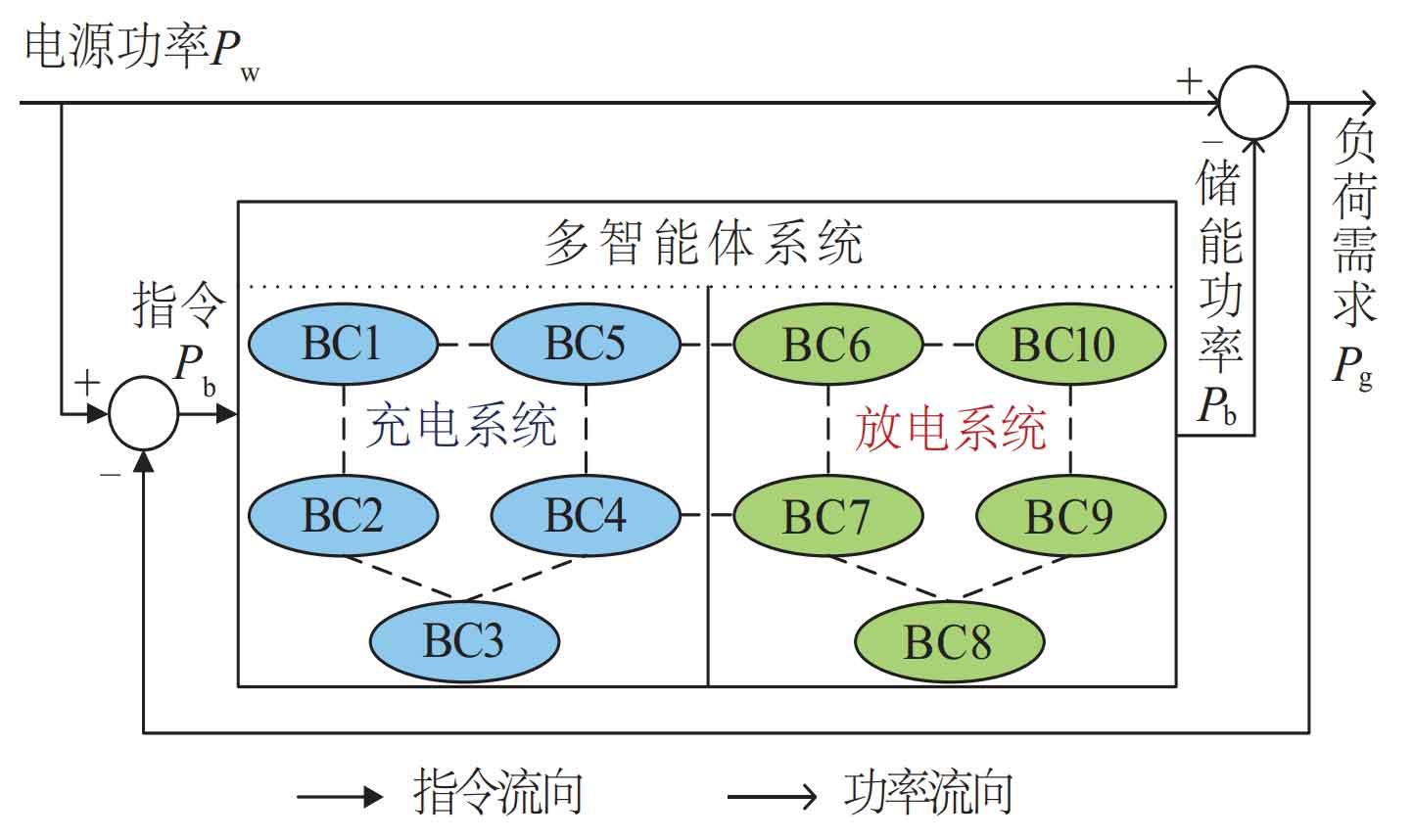
The topology structure of a multi-agent system composed of 10 battery cells is shown in Figure 2. The simulation was conducted using 24-hour data, and the power data is shown in Figure 3. It should be noted that due to the uncertainty of wind power and photovoltaic systems, the battery energy storage system may exhibit significant power fluctuations at certain times, resulting in situations marked at A, B, and C in Figure 3. At this point, the demand for battery energy storage will exceed the rated power of a single subsystem by 2.5 MW.
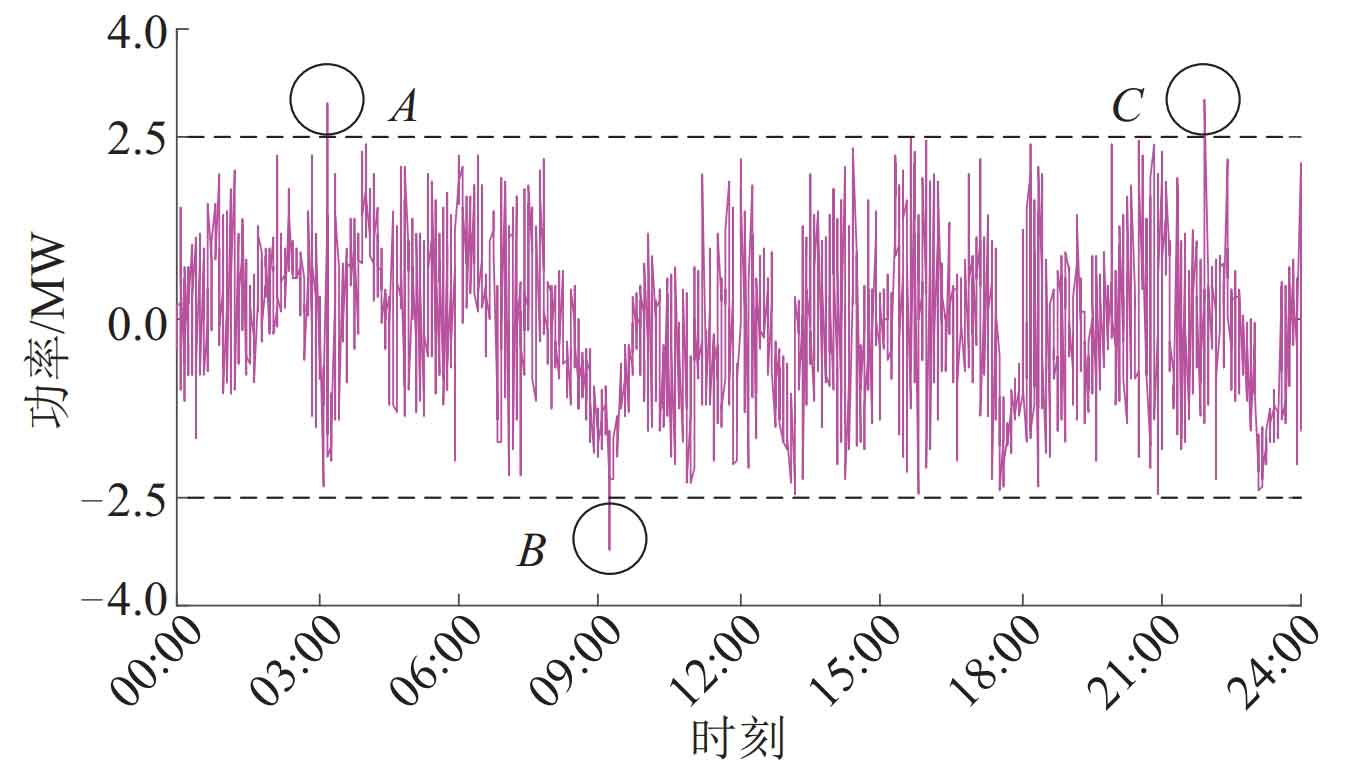
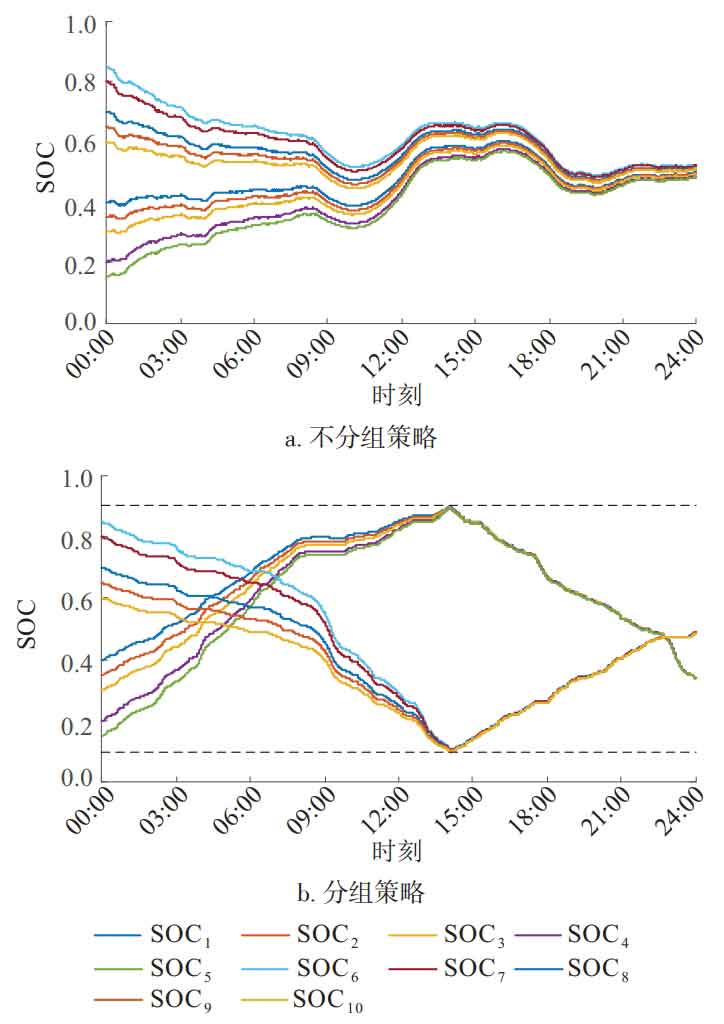
The power curve shown in Figure 4 can be obtained by using the proposed control strategy. From Figure 4, it can be seen that power with P>0 is digested by the charging system, while power with P<0 is digested by the discharge system. When there are three special moments, A, B, and C, as shown in Figure 3, it is necessary to establish a communication connection with another subsystem to jointly undertake power instructions. By using non group equilibrium strategy and group equilibrium strategy respectively, SOC was estimated using methods, and the daily variation curve of SOC was obtained as shown in Figure 5. From Figure 5, it can be seen that although the initial SOC of each battery cell is different for both group balancing and non group balancing strategies, the gap gradually narrows over time, and the SOC of each battery cell gradually approaches equilibrium.
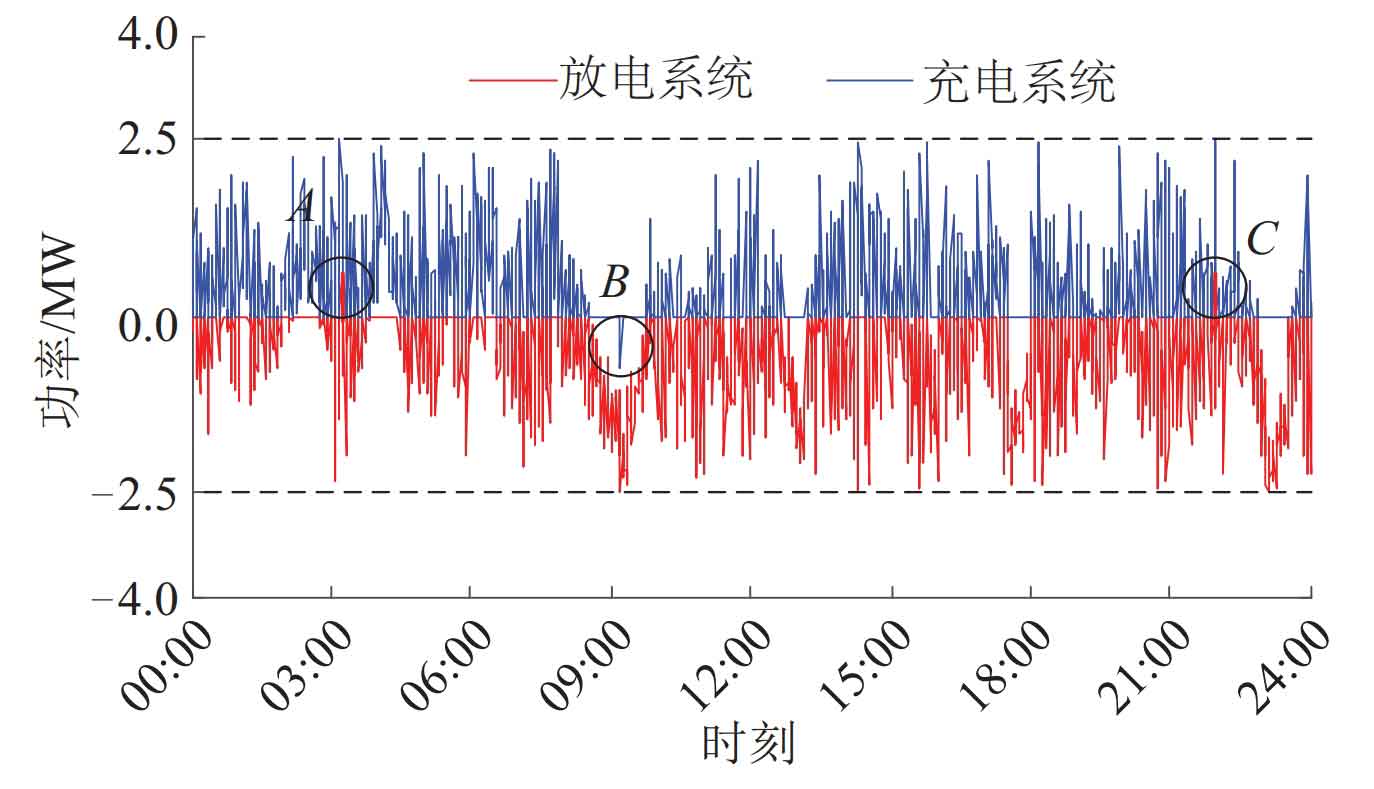
Through comparison, it can be found that: 1) When using the non group balancing strategy, the SOC balancing speed is significantly slower. The SOC of each battery unit tends to 0.5 and only fluctuates around 0.5, which greatly reduces the utilization rate of battery capacity. 2) When using a group balancing strategy, the SOC balancing speed is faster, and all battery cells work in a safe zone. When a certain battery cell SOC in the system reaches the threshold, the two battery systems will exchange “roles”. This strategy can effectively improve the utilization rate of battery capacity.
3.2 Battery Life Analysis
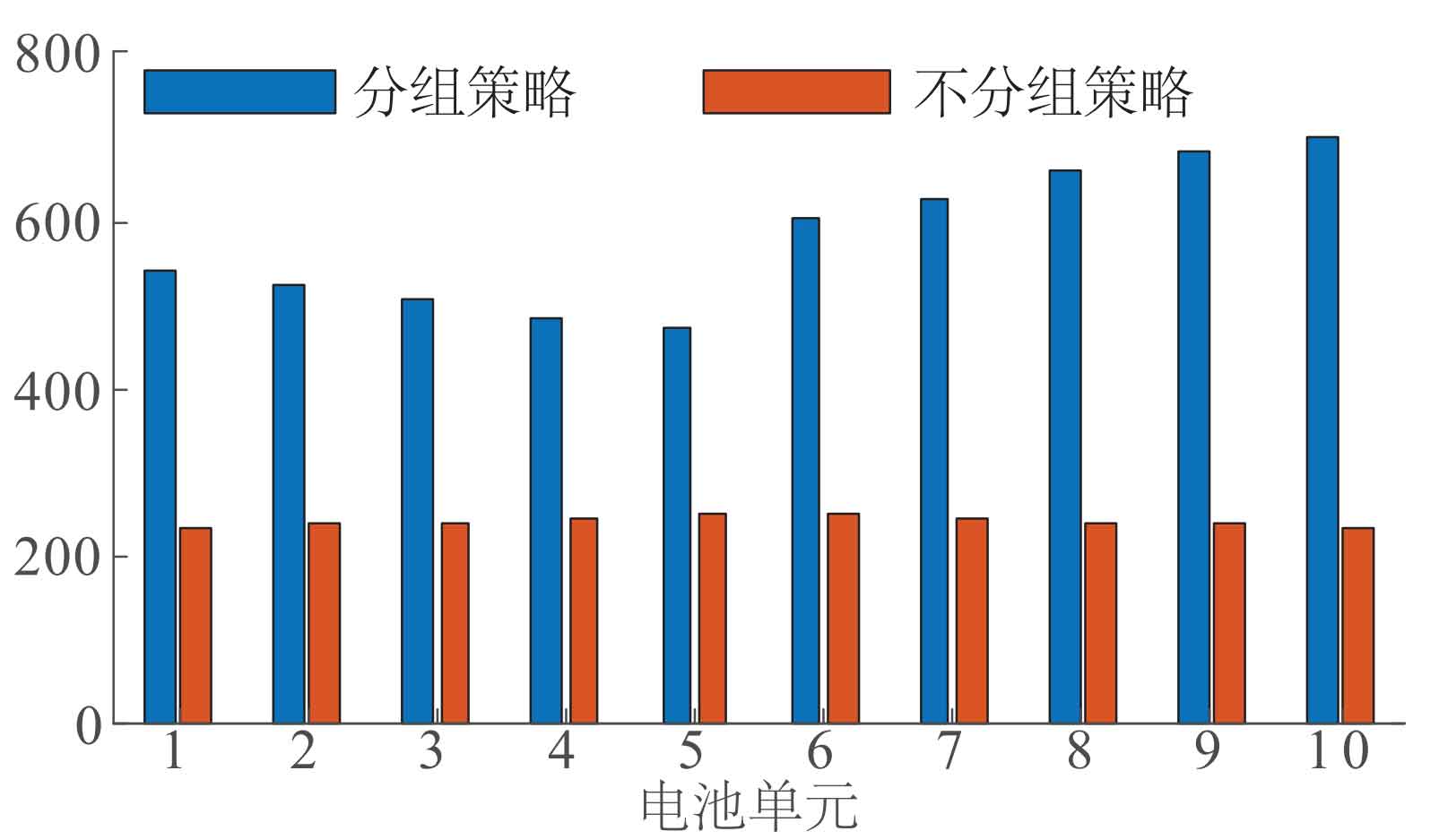
Assuming that the cycle life of each battery unit is 3000 cycles, and the rated charging and discharging depth of the battery is 90%. Using the rain flow counting method, the daily variation curves of SOC shown in Figures 5 and 6a were statistically analyzed. The statistical results were converted into the equivalent number of daily cycles at the rated charging and discharging depth using the method. Then, the lifespan of each battery cell under the group equilibrium strategy and the non group equilibrium strategy were calculated separately, as shown in Figure 6. From Figure 6, it can be seen that under the same conditions, using the non group balancing strategy only results in a battery life of about 250 days, while using the group balancing strategy can achieve a battery life of 500-700 days. This indicates that the proposed MAS based SOC group balancing strategy can extend the battery life to a certain extent.
3.3 Algorithm convergence speed
Taking 5 battery cells in the charging system as an example, perform performance analysis of the algorithm. Set the initial SOC as [0.40, 0.35, 0.30, 0.20, 0.15], power command Pb=2 MW, battery unit capacity C=2 MWh, Nc=7, Np=10, e=0.1. Using a formula, calculate the error of the state variables of each agent after each iteration, and then evaluate the algorithm performance by comparing the convergence speed of traditional multi-agent algorithms with the MPC based multi-agent distributed algorithm proposed in section 2.2.
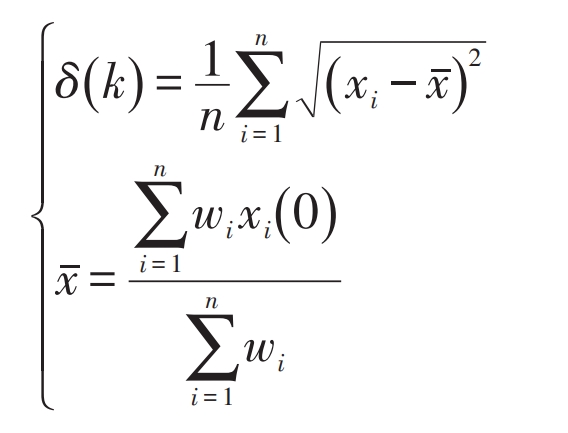
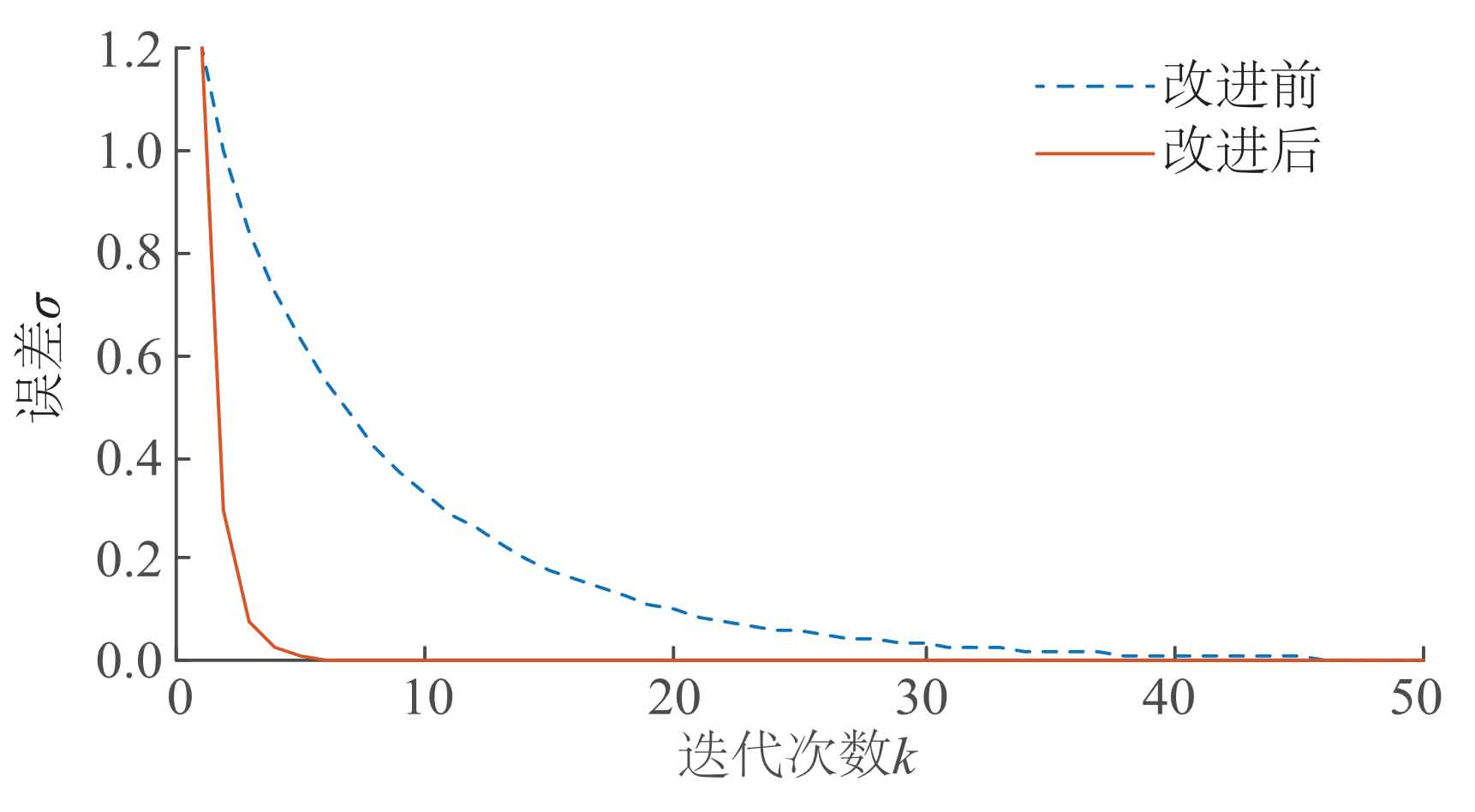
Figure 7 shows the comparison of the convergence speed of the algorithm before improvement (traditional multi-agent distributed algorithm) and after improvement (MPC based multi-agent distributed algorithm). It can be seen that the convergence speed of the improved algorithm is significantly faster than before improvement.
4. Conclusion
Taking a distributed battery energy storage system containing multiple battery energy storage units as the research object, a distributed battery energy storage system collaborative control strategy based on SOC balance is proposed. This strategy can enable each battery unit to achieve SOC dynamic balance during normal charging and discharging processes. To implement this strategy, a MAS based SOC group balancing strategy is first proposed, which uses multi-agent algorithms to achieve SOC balancing; Then, to address the slow convergence speed of traditional multi-agent distributed algorithms, a multi-agent distributed algorithm based on MPC is proposed; Finally, simulation verification was conducted using actual energy storage power data from a certain microgrid, and the following main conclusions were drawn:
1) The SOC group balancing strategy based on MAS can achieve dynamic balancing of SOC in each battery unit, improve the utilization rate of battery capacity, and extend battery life to a certain extent.
2) Compared to traditional multi-agent algorithms, MPC based multi-agent distributed algorithms have faster convergence speed and can meet the real-time control requirements of distributed battery energy storage systems.
