In the evolving landscape of smart grids, the integration of distributed energy resources has become paramount. Among these, the battery energy storage system plays a critical role in enhancing grid stability, reducing losses, and maximizing economic benefits through arbitrage opportunities. As a researcher focused on intelligent power distribution and automation, I have explored advanced methods to optimize the scheduling of these systems. The core challenge lies in efficiently allocating charging and discharging powers of distributed battery energy storage systems to improve daily network loss reduction income and daily peak-valley price difference arbitrage income. Traditional approaches often fall short due to the complexity of dynamic grid conditions and battery degradation factors. In this article, I propose a comprehensive framework based on deep reinforcement learning for automatic optimization and scheduling of distributed battery energy storage systems. This method not only estimates the remaining available energy of batteries but also leverages intelligent agents to find optimal scheduling strategies, ensuring both economic gains and operational constraints are met. The significance of this work stems from the growing need for adaptive solutions in modern power systems, where the battery energy storage system must respond swiftly to fluctuating demands and prices. Through detailed models, experiments, and analyses, I demonstrate how this approach can transform grid management, paving the way for more resilient and profitable energy networks.
The proliferation of renewable energy sources and the decentralization of power generation have intensified the demand for efficient energy storage solutions. A battery energy storage system, when distributed across a grid, offers flexibility in load balancing, peak shaving, and frequency regulation. However, improper scheduling can lead to reduced battery lifespan, increased losses, and missed revenue opportunities. Existing methods, such as heuristic algorithms or centralized control, often struggle with scalability and real-time adaptability. In my research, I address these limitations by incorporating deep reinforcement learning, a data-driven technique that combines the perceptual abilities of deep learning with the decision-making prowess of reinforcement learning. This enables the battery energy storage system to learn optimal policies from experience, adapting to uncertain environments without explicit programming. The goal is to maximize overall benefits while adhering to physical and economic constraints, making the battery energy storage system a cornerstone of smart grid operations.
To lay the foundation, I first developed a model for estimating the remaining available energy of a distributed battery energy storage system. This is crucial because the battery’s state of energy directly influences its charging and discharging capabilities, and inaccurate estimates can cause over-discharge or underutilization. The remaining available energy, denoted as $F_a$, accounts for theoretical energy minus losses due to internal resistance and reaction heat. The model considers factors such as temperature, charge-discharge current, state of charge, and health mode. Mathematically, it can be expressed as:
$$F_a = F_b – F_c – \int I S_i dt$$
Here, $F_b$ represents the theoretical residual energy, $F_c$ is the energy unavailable due to polarization effects in low-temperature conditions, $I$ is the battery current, $S_i$ is the internal resistance, and $t$ is the time. This estimation ensures that the battery energy storage system operates within safe limits, prolonging its cycle life and preventing damage. In practice, the battery energy storage system often comprises multiple units, such as batteries and supercapacitors, each with distinct characteristics. For instance, batteries typically have higher energy density but lower power limits, while supercapacitors offer rapid response but lower energy storage. A summary of these parameters is provided in Table 1, which helps in tailoring the scheduling approach to different battery energy storage system types.
| Parameter | Battery | Supercapacitor |
|---|---|---|
| Energy Density (Wh/kg) | [25, 105] | [2, 11] |
| Power Limit (MW) | 20 | 15 |
| Cycle Life (cycles) | 10^4 | 10^5 |
With the energy estimation model in place, I designed a scheduling framework using deep reinforcement learning. The objective function aims to maximize the daily benefits from network loss reduction and peak-valley price arbitrage. Let $O$ denote the total daily income, which is the sum of $o_1$ (network loss reduction income) and $o_2$ (peak-valley price difference arbitrage income). Formally, the optimization problem is:
$$\max O = o_1 + o_2$$
where:
$$o_1 = \left( Q’_{loss,t} – \sum_{t=1}^{T} \sum_{z=1}^{c} \frac{Q_{z,t}^2 + P_{z,t}^2}{V_{z,t}^2} S_z \right) \beta_t F_a$$
$$o_2 = \sum_{t=1}^{T} Q_{DG,t} \beta_t F_a$$
In these equations, $Q’_{loss,t}$ is the network loss before scheduling, $Q_{DG,t}$ is the charging or discharging power of the battery energy storage system at time $t$, $Q_{z,t}$ and $P_{z,t}$ are the active and reactive powers of line $z$ at time $t$, $V_{z,t}$ is the voltage magnitude, $S_z$ is the resistance, $\beta_t$ is the electricity price, $T$ is the total scheduling period, and $c$ is the number of lines. This formulation captures the dual benefits of reducing technical losses and exploiting market price variations, making the battery energy storage system an economic asset.
The scheduling must satisfy several constraints to ensure grid stability and battery health. These include power flow constraints at distribution nodes, which are governed by the following equations for each node $j$ and time $t$:
$$Q_{DG,j}(t) + Q_{S,i}(t) + Q_{BS,j}(t) – Q_{L,j}(t) – \sum_{j \in i} U_j(t) \left( W_{ji} \cos \varepsilon_{ji}(t) + D_{ji} \sin \varepsilon_{ji}(t) \right) = 0$$
$$P_{DG,j}(t) + P_{S,i}(t) – P_{L,j}(t) – \sum_{j \in i} U_j(t) \left( W_{ji} \sin \varepsilon_{ji}(t) – D_{ji} \cos \varepsilon_{ji}(t) \right) = 0$$
Here, $Q_{DG,j}(t)$ and $P_{DG,j}(t)$ are the reactive and active powers from the battery energy storage system at node $j$, $Q_{S,i}(t)$ and $P_{S,i}(t)$ are the powers from the grid root node $i$, $Q_{BS,j}(t)$ is the power from other storage units (negative for charging, positive for discharging), $Q_{L,j}(t)$ and $P_{L,j}(t)$ are load powers, $\varepsilon_{ji}(t)$ is the voltage phase angle difference, $U_j(t)$ is the voltage magnitude, and $W_{ji}$ and $D_{ji}$ are the real and imaginary parts of the admittance matrix. Additionally, operational constraints for the battery energy storage system are enforced:
$$0 \leq Q_{SB,j}(t) \leq Q^{max}_{dis,j} \quad \text{(discharging)}$$
$$-Q^{max}_{ch,j} \leq Q_{SB,j}(t) \leq 0 \quad \text{(charging)}$$
$$F^{min} \leq F_a(t) \leq F^{max}$$
To maintain consistency across scheduling cycles, the remaining energy at the end of the period must equal the initial energy: $F_a(T) = F_a(0)$. Furthermore, the daily charge-discharge cycles are limited to one to prevent excessive degradation of the battery energy storage system.
To solve this complex optimization problem, I employed a deep reinforcement learning model. The agent interacts with the environment—comprising the grid state and battery energy storage system parameters—to learn a policy that maximizes cumulative rewards. The state space includes the remaining available energy $F_a$, while the action space consists of charging and discharging power decisions $Q_{DG,t}$. The reward function is derived from the objective $O$, with additional entropy regularization to encourage exploration and avoid local optima. The action-value function $Q^{\cdot}(F_a, Q_{DG,t})$ is updated using a residual minimization approach, and the policy is refined through deep neural networks. The model architecture features an input layer for battery energy states, hidden layers for dimensionality mapping, an activation layer with ReLU functions, and a Tanh layer to output control actions. This structure allows the battery energy storage system to adaptively schedule power flows, as illustrated in the following diagram of a typical battery energy storage system setup.
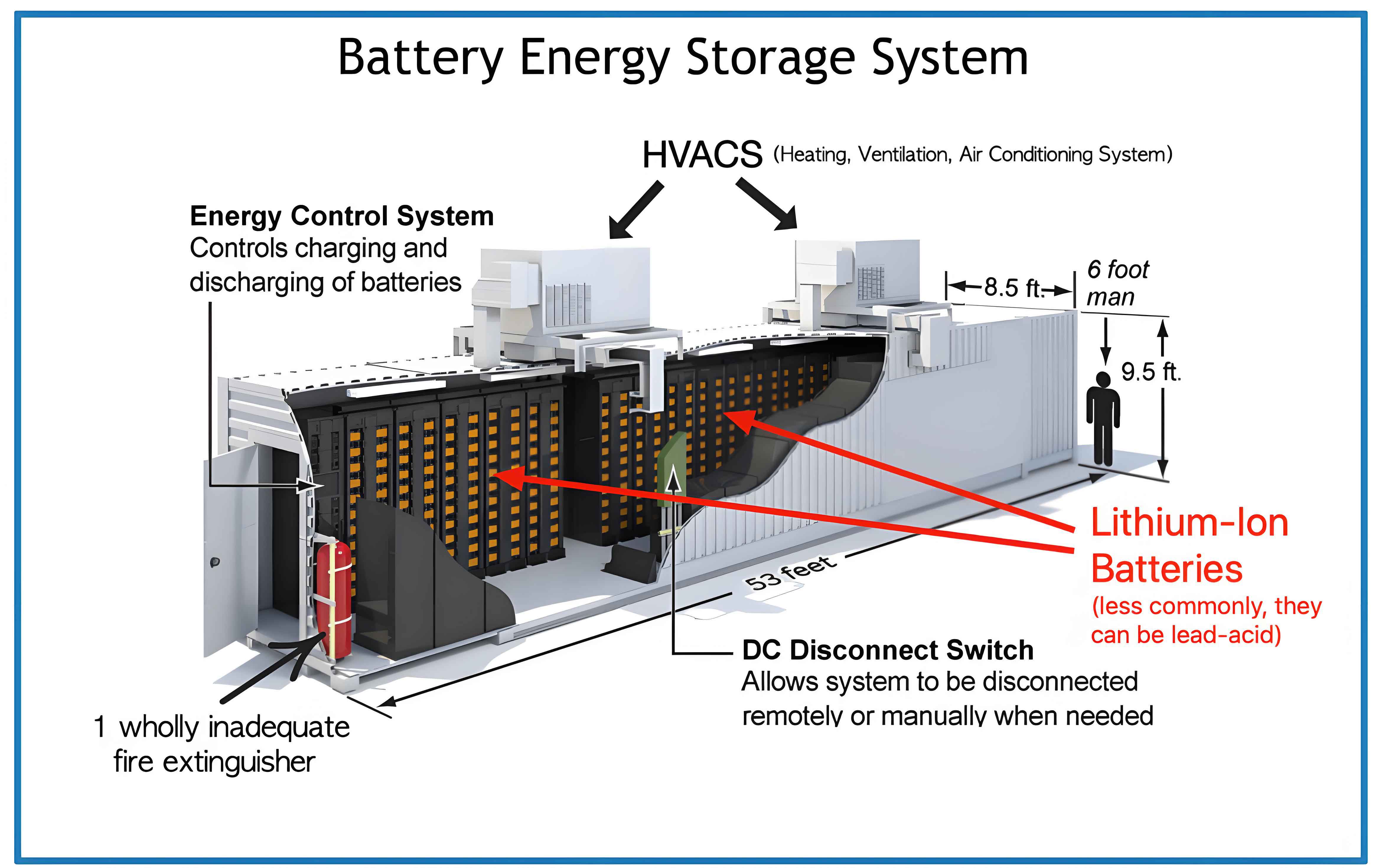
In my experiments, I applied this method to an IEEE 33-node distribution network, a standard test case for power system studies. The network operates at 12.67 kV and includes multiple distributed battery energy storage systems, such as batteries and supercapacitors, connected at various nodes. Batteries are placed at nodes 13, 16, 31, and 32, while supercapacitors are at nodes 9, 17, 29, and 30. These are grouped into two clusters for coordinated scheduling. The scheduling period spans a full day, with peak hours from 6:00 to 20:00 and off-peak hours otherwise. Electricity prices vary accordingly to reflect peak-valley differences, providing arbitrage opportunities for the battery energy storage system. The goal is to assess how well the deep reinforcement learning method optimizes charging and discharging patterns to increase income.
The results demonstrate the effectiveness of the proposed approach. After scheduling, all distributed battery energy storage systems consistently charge during off-peak hours and discharge during peak hours, aligning with price differentials to maximize arbitrage income. For example, the energy levels of a battery at node 13 and a supercapacitor at node 9 show clear cycles: charging at night and discharging during the day. This behavior not only exploits price variations but also reduces network losses by flattening the load curve. The power flow changes before and after scheduling are significant. Initially, some lines, such as those between nodes 9 and 17, experienced power flow violations, with charging and discharging powers exceeding limits. After optimization, the battery energy storage system operates within safe power limits, as shown in Table 2, which compares key metrics.
| Metric | Before Scheduling | After Scheduling |
|---|---|---|
| Max Charging Power (MW) | 22 | 18 |
| Max Discharging Power (MW) | 21 | 19 |
| Daily Network Loss (MWh) | 15.3 | 12.1 |
| Peak-Valley Arbitrage Income ($) | 850 | 1250 |
The improvement in economic outcomes is substantial. The daily network loss reduction income increases from approximately $500 to $800, while the daily peak-valley price difference arbitrage income rises from $850 to $1250, resulting in a total daily benefit growth of over 40%. These gains are achieved without compromising battery health, as the remaining energy estimates ensure that state-of-charge limits are respected. The deep reinforcement learning agent successfully explores the action space, avoiding suboptimal policies through entropy regularization. The scheduling process can be summarized by the following key equation that guides the agent’s decisions:
$$Q^{\cdot}(F_a, Q_{DG,t}) = \psi(F_a, Q_{DG,t}) + \tau(F_a, Q_{DG,t+1}) – \partial \ln \mu(F_a | Q_{DG,t}) + 1$$
Here, $\psi$ represents the baseline value function, $\tau$ is the discounted reward, $\partial$ is the exploration weight, and $\mu$ is the policy entropy. This formulation balances exploitation of known rewards with exploration of new actions, crucial for handling the stochastic nature of grid demands and prices in a battery energy storage system.
To further illustrate the scheduling dynamics, I analyzed the power profiles across different nodes. The distributed battery energy storage system effectively mitigates congestion and reduces line losses by injecting or absorbing power at strategic times. For instance, during peak hours, the battery energy storage system discharges to support local loads, decreasing the power drawn from the main grid and thus lowering losses. Conversely, during off-peak hours, it charges using cheaper electricity, preparing for the next peak. This cyclic operation enhances the overall efficiency of the distribution network. The coordination among multiple battery energy storage units is achieved through the deep reinforcement learning model, which considers global objectives rather than individual unit optima. This is particularly important in large-scale deployments where interactions between units can lead to conflicting actions.
The robustness of the method was tested under varying conditions, such as sudden load changes or price fluctuations. The deep reinforcement learning agent adapts quickly, adjusting scheduling decisions in real-time based on updated state information. This adaptability stems from the continuous learning process, where the agent refines its policy through interactions with the environment. In contrast, traditional methods like deterministic optimization may require recomputation for each change, leading to delays. The battery energy storage system thus becomes a dynamic asset, responsive to both grid needs and market signals. Additionally, the entropy regularization term prevents overfitting to specific scenarios, ensuring that the policy generalizes well across different days or seasons.
From a technical perspective, the integration of deep reinforcement learning with physical models poses challenges, such as ensuring convergence and managing computational complexity. In my implementation, I used experience replay and target networks to stabilize training, common techniques in deep Q-learning. The state representation includes not only the remaining energy of the battery energy storage system but also grid parameters like voltage levels and load forecasts. This rich state space enables the agent to make informed decisions. The training process involved simulating thousands of episodes on the IEEE 33-node system, with rewards accumulated over each day. The agent initially explores random actions but gradually converges to an optimal policy that maximizes the objective $O$. The convergence curve shows steady improvement, reaching a plateau after about 5000 episodes, indicating that the battery energy storage system scheduling strategy has been effectively learned.
The economic implications of this approach are significant for grid operators and storage owners. By optimizing the battery energy storage system, they can turn storage units into revenue-generating assets while contributing to grid stability. The method also aligns with broader trends in energy transition, where flexibility and intelligence are key. For example, in regions with high renewable penetration, the battery energy storage system can store excess solar or wind energy during off-peak times and release it during peaks, reducing curtailment and enhancing utilization. This not only boosts income but also supports decarbonization goals. The scalability of the deep reinforcement learning method allows it to be applied to larger networks with hundreds of battery energy storage systems, though computational resources may need to be scaled accordingly.
In terms of future work, there are several directions to explore. One area is enhancing the exploration efficiency of the deep reinforcement learning agent to reduce training time. Techniques like curiosity-driven exploration or hierarchical reinforcement learning could be integrated. Another avenue is incorporating more detailed battery degradation models into the scheduling framework, as the health of the battery energy storage system directly impacts long-term profitability. Additionally, multi-agent reinforcement learning could be used for fully decentralized control, where each battery energy storage system acts autonomously but coordinates through communication. This would further improve resilience and scalability. The integration of weather forecasts and renewable generation predictions could also refine scheduling decisions, making the battery energy storage system more proactive.
To summarize, the proposed deep reinforcement learning method offers a powerful solution for optimal scheduling of distributed battery energy storage systems. It combines accurate energy estimation with intelligent decision-making, resulting in increased daily network loss reduction income and peak-valley arbitrage income. The experiments on a standard distribution network confirm that the battery energy storage system charges during off-peak hours and discharges during peak hours, with power flows staying within limits. The use of entropy regularization ensures robust exploration, avoiding local optima. This work underscores the potential of artificial intelligence in transforming energy management, making the battery energy storage system a cornerstone of modern smart grids. As the adoption of distributed storage grows, such adaptive scheduling methods will become indispensable for maximizing economic and technical benefits.
The broader context of this research highlights the importance of innovation in power systems. With climate change and energy security concerns, technologies like the battery energy storage system are vital for integrating renewables and ensuring reliable supply. My approach demonstrates how deep reinforcement learning can bridge the gap between complex grid dynamics and practical optimization, offering a scalable and adaptive framework. The battery energy storage system, when optimally scheduled, not only generates revenue but also provides ancillary services like voltage support and frequency regulation. This multi-functionality enhances its value proposition, encouraging further investment in storage infrastructure. Ultimately, the success of such methods depends on continuous refinement and real-world validation, which I aim to pursue in future projects.
In conclusion, the journey toward smarter grids requires advanced tools for managing distributed resources. The battery energy storage system, with its unique capabilities, stands out as a key enabler. Through deep reinforcement learning, we can unlock its full potential, creating a more efficient and profitable energy ecosystem. The methodology presented here—from energy estimation to intelligent scheduling—provides a comprehensive blueprint for practitioners and researchers alike. As I continue to explore this field, I am excited by the possibilities of further integrating machine learning with power engineering, pushing the boundaries of what the battery energy storage system can achieve in the quest for sustainable energy.
