In recent years, the growing demand for energy and the depletion of traditional fossil fuels have driven the search for sustainable alternatives. As a researcher focused on renewable energy systems, I have dedicated significant effort to studying photovoltaic technology, particularly off-grid solar systems. These systems offer a viable solution for remote areas or applications where grid connection is impractical. The off-grid solar system operates independently, converting solar energy into usable electricity without relying on external power networks. This paper presents a comprehensive simulation study of a single-phase off-grid solar system using MATLAB, emphasizing the design, control strategies, and performance analysis. The off-grid solar system is crucial for decentralized power generation, and its efficiency depends on effective energy management and control.
The core of an off-grid solar system involves converting DC power from photovoltaic panels to AC power for local loads. This process requires a two-stage topology: a DC/DC converter to boost the voltage and a DC/AC inverter to produce AC output. In my research, I modeled this system to analyze the interactions between components, such as the photovoltaic modules, input filtering capacitors, and the inverter. A key challenge in off-grid solar systems is maintaining stable DC bus voltage and high-quality AC output under varying solar conditions. Through MATLAB simulations, I implemented double closed-loop control strategies using PI regulators to achieve this stability. The off-grid solar system’s performance was evaluated based on output waveform quality, voltage regulation, and total harmonic distortion.
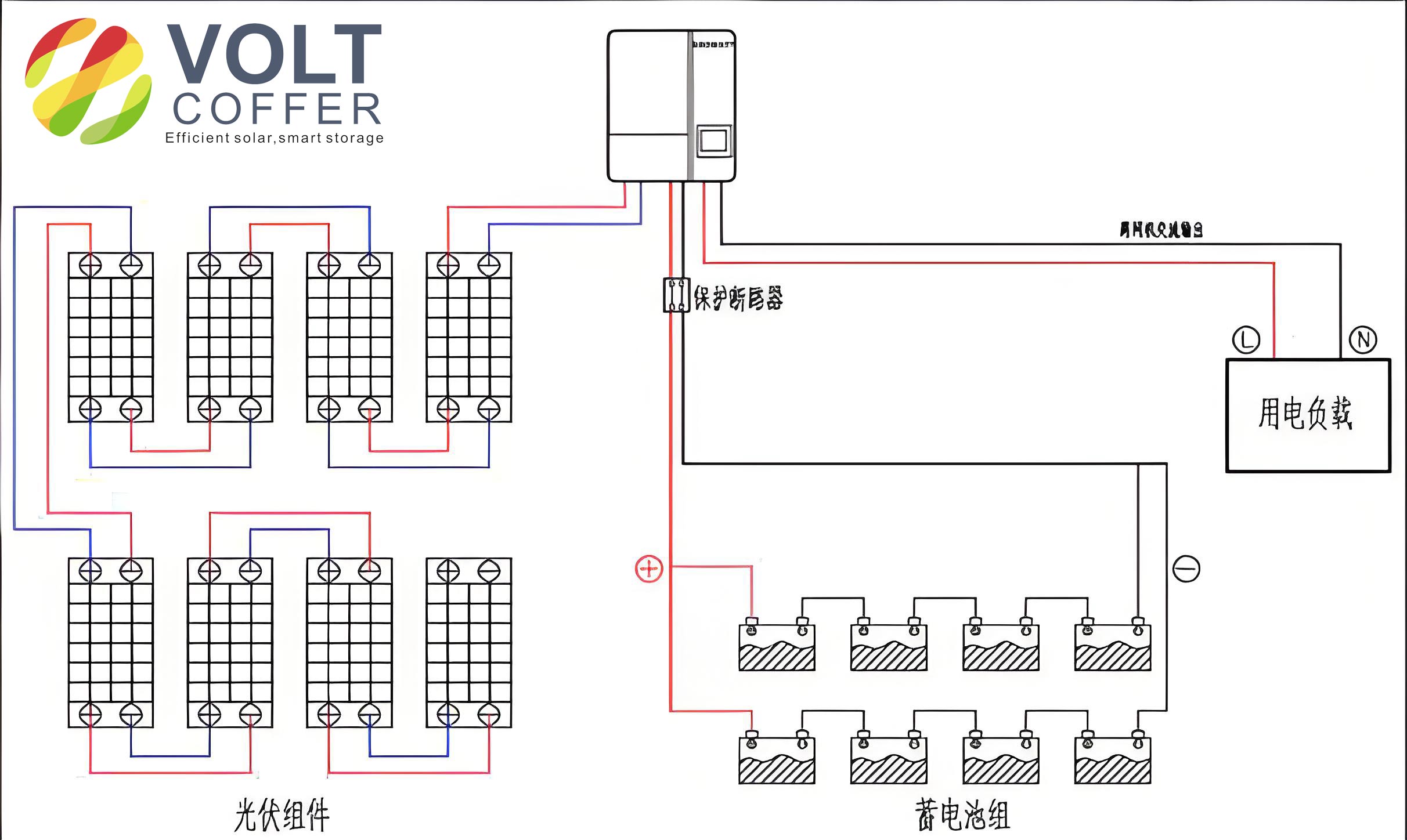
To understand the off-grid solar system’s operation, it is essential to delve into its main circuit topology. The system consists of a photovoltaic array, a DC/DC Boost converter, and a DC/AC full-bridge inverter. The photovoltaic array generates DC power, which is often at a low voltage level. The Boost converter steps this voltage up to a higher DC level suitable for inversion. The full-bridge inverter then converts the DC to AC, which is filtered to produce a sinusoidal output for off-grid loads. The mathematical representation of the Boost converter’s operation can be derived from its inductor current dynamics. For instance, the change in inductor current during the switch-on period is given by:
$$ \Delta i_L = \frac{U_c}{L} \cdot T_{\text{on}} = \frac{U_c}{L} \cdot d T $$
where \( \Delta i_L \) is the inductor current change, \( U_c \) is the capacitor voltage, \( L \) is the inductance, \( d \) is the duty cycle, and \( T \) is the switching period. This equation highlights how the duty cycle controls the energy transfer in the off-grid solar system. The inverter stage uses pulse-width modulation (PWM) to generate AC output. The output voltage and current for a resistive load can be expressed as:
$$ u_o = U_{om} \sin(\omega t) $$
$$ i_o = I_{om} \sin(\omega t) $$
where \( U_{om} \) and \( I_{om} \) are the peak voltage and current, respectively, and \( \omega \) is the angular frequency. The instantaneous output power is then:
$$ p_o = u_o i_o = \frac{p_{om}}{2} (1 – \cos(2\omega t)) $$
This shows a power ripple at twice the grid frequency, which must be managed by the off-grid solar system’s energy storage elements.
Energy coupling in an off-grid solar system involves balancing power between the photovoltaic input, filtering capacitors, and the inverter. The power relationship can be analyzed using energy conservation principles. Let \( P_{pv} \) be the photovoltaic output power, \( P_i \) the inverter input power, and \( P_c \) the coupling power of the filter capacitor. The energy balance over a period \( T \) is:
$$ E = \int_t^{t+T} P_{pv} \, dt + \Delta E_c $$
where \( E \) is the energy input to the inverter and \( \Delta E_c \) is the change in capacitor energy. If inverter losses are neglected, \( E \) equals the output energy. For the Boost converter operating in continuous conduction mode (CCM), the input energy per switching cycle is:
$$ e = \frac{1}{2} L (\Delta i_L)^2 $$
and the instantaneous power input to the inverter is:
$$ p = e f_s $$
where \( f_s \) is the switching frequency. Thus, the energy over a period is:
$$ E = \int_t^{t+T} p \, dt $$
This formulation allows precise power control in the off-grid solar system by adjusting the duty cycle and switching period. To illustrate the parameter relationships, Table 1 summarizes key variables in the energy coupling analysis.
| Parameter | Symbol | Description |
|---|---|---|
| Photovoltaic Power | \( P_{pv} \) | Output power from solar panels |
| Inverter Input Power | \( P_i \) | Power fed into the inverter |
| Coupling Power | \( P_c \) | Power handled by filter capacitor |
| Inductance | \( L \) | Boost converter inductance |
| Duty Cycle | \( d \) | Switch duty ratio in Boost converter |
| Switching Frequency | \( f_s \) | Frequency of PWM switching |
Control strategies are vital for the stability and performance of an off-grid solar system. I employed a double closed-loop control approach, with an outer voltage loop and an inner current loop. The DC/DC Boost converter uses voltage feedback to maintain the DC bus voltage at a setpoint, such as 400V. The error between the reference voltage \( U_{\text{ref1}} \) and the measured DC voltage \( U_{dc} \) is processed by a PI controller. The PI controller output modulates the PWM signals for the Boost switch. The transfer function of a PI controller can be written as:
$$ G_c(s) = K_p + \frac{K_i}{s} $$
where \( K_p \) is the proportional gain and \( K_i \) is the integral gain. For the DC/AC inverter, a similar voltage control loop is used to regulate the AC output. The reference AC voltage \( U_{\text{ref2}} \) is compared to the actual output \( U_o \), and the error is fed into another PI controller to generate PWM signals for the inverter switches. This ensures a stable sinusoidal output with low distortion. The off-grid solar system’s control框图 can be represented mathematically, emphasizing the interdependence of the loops. For instance, the DC bus voltage dynamics can be modeled as:
$$ C_{dc} \frac{dU_{dc}}{dt} = I_{pv} – I_i $$
where \( C_{dc} \) is the DC bus capacitance, \( I_{pv} \) is the photovoltaic current, and \( I_i \) is the inverter input current. This equation shows how capacitor energy buffers power fluctuations in the off-grid solar system.
To validate the off-grid solar system design, I conducted extensive simulations in MATLAB/Simulink. The model included the photovoltaic array, Boost converter, full-bridge inverter, and LC filter. Parameters were set based on typical off-grid applications: DC bus voltage reference at 400V, AC output peak voltage at 311V (220V RMS), frequency at 50Hz, Boost inductor at 2.2mH, DC bus capacitor at 1000μF, filter inductor at 5.5mH, filter capacitor at 30μF, and switching frequency at 10kHz. The simulation results demonstrated the effectiveness of the control strategies. The AC output voltage and current waveforms were nearly sinusoidal, with minimal phase difference, indicating good power factor. The DC bus voltage remained stable around 400V, with minor deviations due to load changes. A Fast Fourier Transform (FFT) analysis revealed a total harmonic distortion (THD) of less than 1%, which is acceptable for off-grid solar systems. Table 2 provides a summary of the simulation parameters and performance metrics.
| Parameter | Value | Unit |
|---|---|---|
| DC Bus Voltage | 400 | V |
| AC Output Voltage (Peak) | 311 | V |
| Frequency | 50 | Hz |
| Boost Inductance | 2.2 | mH |
| DC Bus Capacitance | 1000 | μF |
| Filter Inductance | 5.5 | mH |
| Filter Capacitance | 30 | μF |
| Switching Frequency | 10 | kHz |
| THD | 0.54 | % |
The off-grid solar system’s performance can be further analyzed using mathematical models of power flow. The instantaneous power balance equation accounts for losses and storage. For example, the photovoltaic output power \( P_{pv} \) varies with solar irradiance and temperature, modeled as:
$$ P_{pv} = V_{pv} I_{pv} $$
where \( V_{pv} \) and \( I_{pv} \) are the photovoltaic voltage and current. The inverter efficiency \( \eta \) affects the output power:
$$ P_o = \eta P_i $$
In the off-grid solar system, the LC filter attenuates harmonics, and its transfer function for the output voltage can be expressed as:
$$ \frac{U_o(s)}{U_i(s)} = \frac{1}{L_s C_s s^2 + 1} $$
where \( L_s \) and \( C_s \) are the filter inductance and capacitance. This second-order system contributes to the overall stability. The PI controller parameters were tuned using Ziegler-Nichols methods to achieve optimal response. For instance, the proportional gain \( K_p \) and integral time constant \( T_i \) were adjusted to minimize overshoot and settling time in the DC bus voltage. The off-grid solar system’s robustness was tested under step changes in load and solar input, showing that the double-loop control maintained performance.
In conclusion, the simulation of the off-grid solar system using MATLAB provides valuable insights into its operation and control. The two-stage topology with Boost converter and full-bridge inverter effectively handles voltage conversion and inversion. The energy coupling analysis highlights the importance of capacitors in balancing power, and the double closed-loop PI control ensures voltage stability and low distortion. The off-grid solar system demonstrated reliable performance in simulations, with THD below 1% and stable DC bus voltage. This approach can be extended to more complex scenarios, such as integrating battery storage or adapting to variable loads. Future work could focus on real-time implementation and optimization for cost reduction. Overall, the off-grid solar system represents a promising solution for sustainable energy access, and MATLAB serves as a powerful tool for its development and validation.
Throughout this study, I have emphasized the versatility of the off-grid solar system in various applications. By leveraging MATLAB’s simulation capabilities, I could iterate designs quickly and verify control strategies without physical prototypes. The use of mathematical models and tables, as shown, facilitates a deeper understanding of the system dynamics. As renewable energy adoption grows, off-grid solar systems will play a critical role in achieving energy independence, and continued research in this area is essential for innovation and improvement.
