With the continuous deepening of the “dual carbon” goal, the proportion of new energy represented by wind power and photovoltaic in the power system is constantly increasing, and the problem of insufficient absorption capacity of new energy and wind and solar waste is becoming increasingly prominent. Energy storage can assist in alleviating the problems faced by new energy, but the long investment return cycle, severe idle resources, and huge initial investment costs limit its large-scale application. In the demand for new energy consumption scenarios, it is impossible to achieve decoupling of electricity generation and consumption in time and space, and it is difficult to provide flexible adjustment resources. In view of this, studying energy storage technologies and their business models for new energy consumption scenarios is an important support for breaking through the bottleneck of the development of new power systems and helping the power industry achieve the “dual carbon” goal. As a new business model, shared energy storage combines the sharing economy with energy storage, and achieves sharing by separating ownership and usage rights of energy storage, providing flexible regulatory resources for new energy consumption and achieving decoupling of electricity generation and consumption in time and space.
According to different application scenarios, it can be divided into power generation side, grid side, and user side, and energy storage needs to meet different regulation needs in each scenario. On the user side, energy storage can reduce the electricity cost of users based on the time of use electricity price, and meet their energy needs by improving the load distribution of users. On the power grid side, energy storage is used to meet the regulation needs of the power grid, ensuring the stable operation of the power system. It is proposed to use energy storage to track the day ahead scheduling plan and participate in grid frequency modulation to provide frequency support for the grid. On the power generation side, energy storage can suppress power fluctuations,
Enhance the friendly grid connection capability of new energy. Based on different complementary methods of wind and solar energy, energy storage is configured with the goal of suppressing the volatility of new energy power stations after grid connection. A shared energy storage cooperation model is proposed based on the construction of a shared network based on the excess and insufficient power generated by each new energy power station, and the self allocation and storage of new energy power stations on the power generation side. In the scenario of new energy consumption, the introduction of shared energy storage on the power generation side can not only improve the consumption capacity of new energy, but also benefit the regulation ability of energy storage, which has a positive effect on the stable operation of a high proportion of new energy power systems.
To optimize the configuration of energy storage, a cloud energy storage operator is established to integrate limited distributed energy storage resources and achieve the sharing of energy storage resources. Propose a centralized shared energy storage operation model for new energy consumption scenarios, and design an evaluation index system for its operational status accordingly. Propose a capacity configuration and operation optimization plan for multi-agent joint investment and construction of shared energy storage based on energy cell networks. The two-level programming model is used to optimize the capacity configuration and operation strategy of user side energy storage. The upper layer optimizes the energy storage capacity and power with the goal of maximizing economic benefits throughout the entire life cycle of user side energy storage, while the lower layer optimizes the energy storage operation strategy with the goal of optimizing the daily operation economy of energy storage. Considering user demand management, a two-stage optimization method is adopted to optimize and schedule energy storage. From an economic perspective, an energy storage optimization configuration model was constructed for distributed energy storage with the goal of minimizing initial investment and operation and maintenance costs. The energy storage capacity problem was optimized and calculated using intelligent algorithms. A bilevel programming model was established to solve the multi-objective problem of minimizing the operating cost of energy storage power stations and optimizing the operating economy of micro energy networks using the Karush Kuhn Tucker Method (KKTM). Propose a multi-objective optimization configuration for shared energy storage in multiple microgrids and an improved Shapley value method for fair allocation of costs. The optimal solution is obtained using the non dominated sorting genetic algorithm (NSGA – II) and fuzzy membership function. A capacity optimization configuration model for shared energy storage systems under the interconnection of multiple Regional Integrated Energy Systems (RIES) is proposed, and genetic algorithms are used to optimize the capacity and charging and discharging power of shared energy storage. A cooperative game model for shared energy storage is established based on the generalized Nash bargaining theory, taking into account the total net profit of each user throughout the entire life cycle of shared energy storage and its impact on the power flow of the distribution network.
The above content is mainly based on microgrid scenarios, and research is limited in the context of new energy consumption scenarios. There is relatively little research on the optimization configuration of shared energy storage considering new energy consumption scenarios, including multiple new energy stations, new energy consumption rates, and economics. At the same time, energy storage plays an important role in the consumption of new energy, but with the increase of the number and installed capacity of new energy stations participating in sharing, the optimization configuration and operation of distributed shared energy storage are difficult to achieve. At present, in terms of optimizing the configuration of shared energy storage, factors such as the consumption rate of new energy, the cost of energy storage investment and construction, and the investment return period have attracted much attention. With the increase of shared energy storage service objects, nonlinear variables have also increased, posing higher requirements for the accuracy and convergence speed of optimization configuration algorithms.
Based on the demand and output characteristics of new energy grid connection, an optimization configuration model was established with the goal of maximizing the benefits of shared energy storage. Under the constraints of shared energy storage operation status, grid connection demand, and new energy output, the whale optimization algorithm (WOA) was used to solve the optimization configuration results, solving the multi-objective and nonlinear constraint problems in the optimization configuration model. The example analyzed the impact of new energy consumption scenarios on the optimization configuration of shared energy storage, Verified the feasibility of the shared energy storage optimization configuration model proposed in this article.
1.Shared energy storage operation mode
Shared energy storage refers to the utilization of energy storage in a shared manner, achieving the separation of ownership and usage rights of energy storage resources, and enabling flexible and efficient interaction among all parties involved in this mode. At present, shared energy storage on the power generation side is mainly divided into two basic structures: decentralized and centralized. Decentralized shared energy storage refers to sharing surplus energy storage resources to provide energy storage services to other entities or the power grid while meeting their own needs. Centralized shared energy storage can be jointly funded and constructed by multiple new energy stations, or invested and constructed by third-party entities for profit purposes. In the face of increasingly complex new energy power systems, the number of new energy stations and energy storage needs are constantly increasing. The existing decentralized energy storage is difficult to achieve flexible resource regulation needs, and centralized energy storage can significantly reduce the complexity of decentralized shared energy storage. Optimizing the allocation of energy storage resources is beneficial for improving energy storage utilization and investment willingness, and is more conducive to its commercial operation. Therefore, this article focuses on centralized shared energy storage as the research object, The basic structure diagram is shown in Figure 1.

The centralized shared energy storage on the power generation side can effectively respond to various regulatory needs through centralized control and allocation of energy storage resources. By utilizing the spatiotemporal complementary characteristics of various regulatory needs, the resource utilization rate of centralized shared energy storage can be improved. While reducing the investment cost of energy storage resources, the economic efficiency of operation can be improved to shorten the return period of energy storage investment. Centralized shared energy storage services are provided for new energy stations. When the output of new energy stations exceeds the grid connection demand, in order to avoid a large amount of wind and light waste, energy storage is used to store the remaining electricity; When the output of new energy cannot meet the grid connection demand, energy storage is used to compensate for the power shortage caused by insufficient output, in order to ensure the dynamic balance between new energy output and grid connection demand, and improve the new energy consumption capacity.
2.Shared Energy Storage Optimization Configuration Model
The sharing mode of energy storage breaks the isolated state between the energy storage equipment and energy storage needs of each energy storage entity under the “self built, self stored, and self used” mode. Based on the spatiotemporal complementary characteristics of multiple regulatory needs, it reduces the idle and waste of energy storage resources and reduces the sunk cost of energy storage. The optimization configuration of shared energy storage in the context of new energy consumption is based on minimizing the investment cost of energy storage. By improving the utilization rate of energy storage resources and maximizing the economic benefits of energy storage, we ensure the consumption of new energy and reduce the amount of wind and light waste.
2.1 Objective function
The construction cost of energy storage investment is the main factor limiting its large-scale development. Reducing the cost of energy storage investment and utilizing limited energy storage resources to achieve maximum economic benefits are the driving forces for the development of shared energy storage. Shared energy storage services are provided to new energy stations in the context of new energy consumption scenarios. Based on this, the objective function is to maximize the typical daily operating revenue of shared energy storage, and to optimize the allocation of energy storage capacity, maximum charging and discharging power, and charging and discharging power at different time periods for shared energy storage stations. Considering the investment cost and operation and maintenance cost of energy storage, the service income obtained from providing energy storage services, in order to support the income of grid connection demand for new energy stations, as well as the abandonment cost of new energy stations caused by insufficient energy storage configuration under the premise of considering economy, a shared energy storage optimization configuration model has been established. The objective function is:
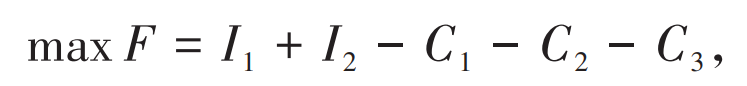
In the formula: I1 is the service income obtained from providing energy storage services for new energy stations by energy storage power stations; I2 represents the revenue generated by energy storage stations to support the demand for new energy grid connection; C1 represents the investment cost of centralized shared energy storage; C2 represents the cost of shared energy storage operation and maintenance; C3 is the penalty cost for abandoning wind and light during the optimal configuration of energy storage economy. The service fee for shared energy storage power stations is calculated based on the actual charging capacity:
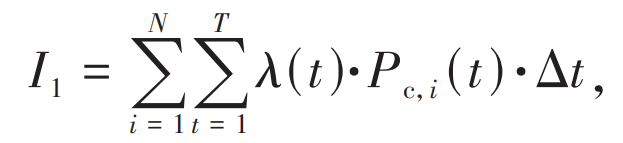
In the formula: N represents the total number of new energy stations; T is the total operating hours of typical daily shared energy storage; λ (t) Unit power service fee for providing energy storage services to new energy stations during the t period of shared energy storage; Pc, i (t) is the charging power of the i-th new energy station during the t-th period; Δ T is the duration of a single energy storage.
There is volatility in the output of new energy. When the output of new energy cannot meet the demand for grid connected power, energy storage discharge is used to compensate for the shortage of grid connected power. For economic considerations, the shared energy storage benefits during the discharge process that supports the grid connection demand of new energy stations are:
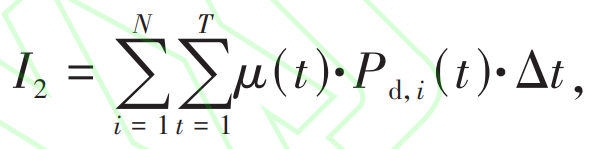
In the equation: μ (t) The unit power price for discharge during the t-th period of energy storage; Pd, i (t) is the discharge power of the i-th new energy station during the t-th period.
Energy storage investment is an important expenditure in the construction process of shared energy storage investment, which includes power investment cost and capacity investment cost. The investment cost model for energy storage power stations is:

In the formula, PESS and EESS respectively represent the power and capacity of energy storage; CP and cE are the unit investment costs of energy storage power and capacity, respectively.
Considering the huge investment cost in the early stage of energy storage construction and the impact of time value, it is necessary to modify and convert the investment cost of energy storage. The correction conversion coefficient is:
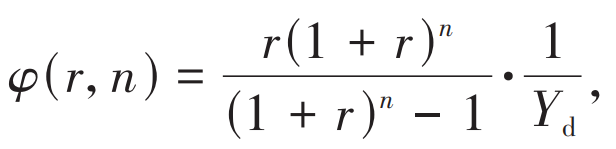
In the formula, r is the benchmark discount rate; N is the operating life of the energy storage power station; Yd is the number of days in a year.
According to equation (5), the conversion coefficient for investment cost correction is calculated as follows:
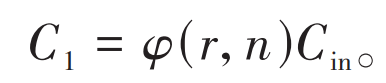
During the operation and maintenance of energy storage, it is necessary to consider its power and total amount of charge and discharge. Therefore, the cost of energy storage operation and maintenance is:

In the formula, kO is the coefficient of daily operation and maintenance cost per unit power of the energy storage power station; KM is the daily operation and maintenance cost coefficient of energy storage unit capacity; QESS is the total daily charge and discharge amount of energy storage.
Due to the difficulty in determining the daily operation and maintenance cost coefficients of the unit power and unit capacity of the energy storage system, the operation and maintenance costs are generally estimated approximately at a certain proportion of the initial investment, namely:
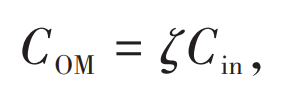
In the equation: ζ Is the maintenance coefficient for energy storage operation.
When optimizing the configuration of shared energy storage, it is necessary to consider the consumption of new energy and optimize the configuration based on the economy of new energy consumption and storage. Therefore, the penalty cost of power abandonment is introduced, which is:
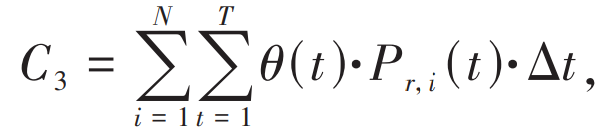
In the equation: θ (t) The penalty cost for unit power curtailment during the t-th period; Pr, i (t) is the abandoned power of the i-th new energy station during the t-th period.
2.2 Constraints
When optimizing the configuration of shared energy storage for new energy consumption scenarios, network and equipment losses are ignored, and the output and grid connection requirements of new energy stations participating in shared energy storage, the state of charge of shared energy storage, and the charging and discharging power of energy storage are considered to determine the constraints that meet the shared energy storage optimization configuration model.
As a joint system, new energy stations and shared energy storage utilize energy storage to suppress the randomness and volatility of new energy output, and absorb peak electricity generated by new energy through energy storage charging. Energy storage discharge compensates for the shortage of grid connected power. The constraints it meets are:
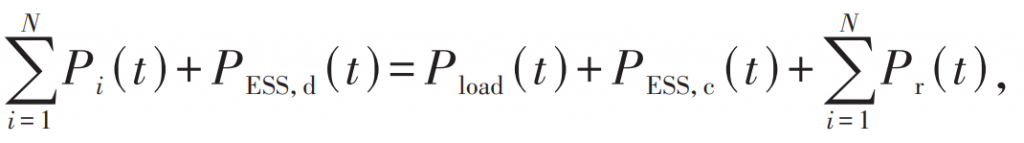
In the formula: Pi (t) is the power generated by the i-th new energy station during the t-th period; PESS, c (t), PESS, d (t) respectively represent the charging and discharging power of the shared energy storage station during the t-th period; Pload (t) is the total power demand for grid connection in time period t; Pr (t) is the total power abandoned during the t-th period. Among them, the shared energy storage charging and discharging power has the following relationship:
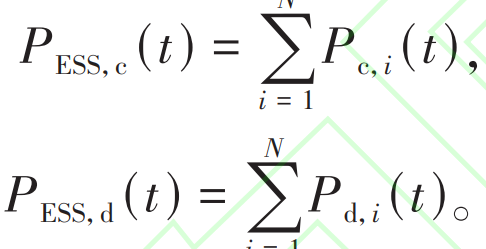
During the charging and discharging process of centralized shared energy storage, it is necessary to consider the charging and discharging status and power. In order to comply with the actual operation situation, the constraint conditions are:

In the equation: σ C (t) and σ D (t) represents the charging and discharging status of the i-th new energy station of the shared energy storage station during the t-th period.
According to the constraints of shared energy storage power stations, the constraint relationships that exist for each new energy station can be obtained as follows:
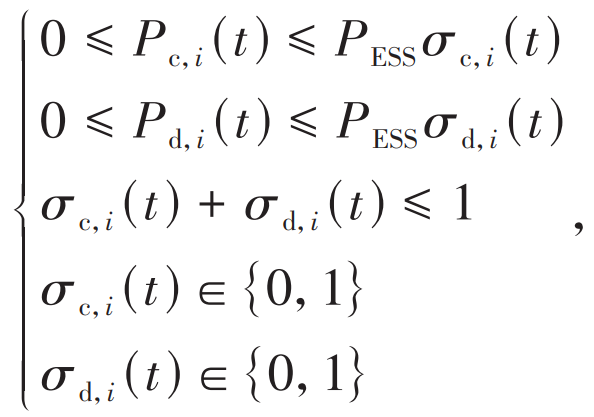
In the equation: σ c. I (t) and σ d. I (t) represents the charging and discharging states of the i-th new energy station during the t-th period; PESS is the maximum charging and discharging power required for new energy stations.
During the operation of shared energy storage power plants, the charging and discharging status will cause continuous changes in the energy storage capacity, and the energy storage capacity will affect the optimized configuration of shared energy storage. Therefore, the economic efficiency of continuous operation and optimized configuration of energy storage is ensured through the charging status and charging and discharging depth of energy storage. The constraints are:

In the formula, SOC min and SOC max are the minimum and maximum states of charge for shared energy storage, respectively; SOC (t) is the state of charge of the centralized shared energy storage power station during the t-th period; η ESS, c and η ESS and d respectively represent the charging efficiency and discharge efficiency of shared energy storage. Equation (15) reflects the relationship between the depth of shared energy storage charging and discharging and the actual state of charge, while Equation (16) reflects the relationship between the state of charge of the t-th period of shared energy storage and the charging and discharging of the previous and current moments.
3.Optimization configuration method for shared energy storage
In the shared energy storage optimization configuration model, the generation power and grid connected power demand of new energy stations are important influencing factors on the charging and discharging power and charging and discharging point status of energy storage stations, while the maximum charging and discharging power and capacity of energy storage stations are influenced by the actual charging and discharging power and charging and discharging status of energy storage stations. In the process of optimizing shared energy storage configuration, there are a large number of nonlinear constraints, and the accuracy and speed of the optimization configuration model will affect the optimization configuration of energy storage. Therefore, in the decision-making process of optimizing the allocation of shared energy storage for new energy consumption, improved WOA is used to obtain the optimal solution.
3.1 WOA
WOA simulates the unique bubble web foraging behavior of whales, constantly surrounding and spiraling towards prey during the process of searching for prey and obtaining prey information, and ultimately capturing prey to obtain the optimal solution to the problem. Due to the fact that WOA is divided into three stages: surround predation, spiral update, and prey search, it has the disadvantages of low solving accuracy, slow convergence speed, and easy falling into local optima. By using quasi reverse learning to initialize the population, using nonlinear convergence factors to update the surround predation stage, adaptive weight strategy, and random difference mutation strategy to prevent falling into local optima, WOA is improved.
During the encirclement and predation stage, the whale population indirectly and continuously moves towards the prey by obtaining prey location information, causing the closest whale individual in the population (the current optimal solution) to approach the prey. In the actual solution process, the global optimal solution of the problem corresponds to the position of the prey. At this stage, the mathematical model used to simulate whale predation behavior is:
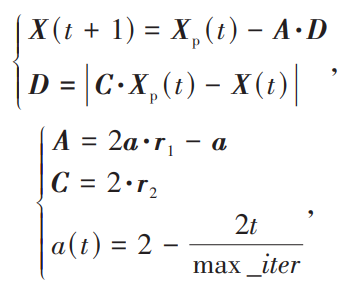
In the formula: t is the number of iterations; X (t) is the position vector of the individual whale; Xp (t) is the prey position vector; A and C are coefficient vectors, respectively, and the specific calculation process is shown in equation (18); R1 and r2 are random vectors within the range of [0,1], respectively; A is a coefficient vector related to the number of iterations, composed of a (t); Max_ Iter is the maximum number of iterations.
In the spiral update stage, with the prey as the center, whales approach the prey through continuous spiral ascent, ultimately achieving the goal of capturing the prey. By calculating the distance between individual whale and prey positions in the population, the distance is reduced in a spiral manner to update the individual’s position. The position update formula is:
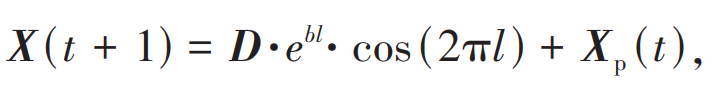
In the formula: b is the constant that defines the spiral coil; L is a random number within the range of [-1, 1].
To ensure the synchronization of contraction and spiral updates, the probability p is used to determine the position update mode of whale individuals. Assuming that the probability of both modes occurring is 50%, namely:
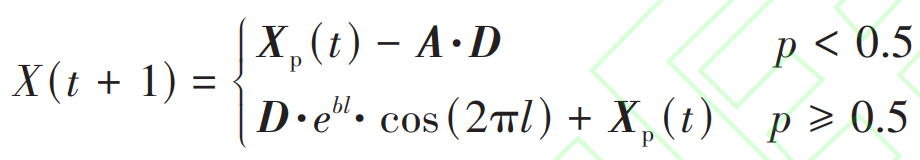
In the formula, p is a random number within the range of [0,1].
During the hunting phase, whales randomly select the desired individuals from the population to update their position by exploring clues about their prey. The expression is:
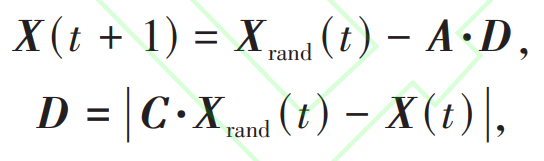
In the formula, Xrand (t) is the position vector of randomly selected whale individuals in the current population.
3.2 Improving WOA
To ensure better initialization of population individuals, quasi reverse learning is introduced on the basis of WOA, combining random solutions with quasi reverse solutions to select the optimal solution, in order to achieve diversity and fast convergence of the population. The mathematical model is:
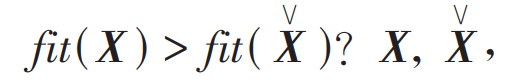
In the equation, fit is the fitness function; X and X ∨ are individual vectors generated by random and quasi reverse learning, respectively.
In the whale population, the position of the i-th whale in the d-dimensional space is Xi=(x1i, x2i,…, xdi), and the individual positions generated by quasi reverse learning are composed of quasi directional solutions. The solution method is as follows:
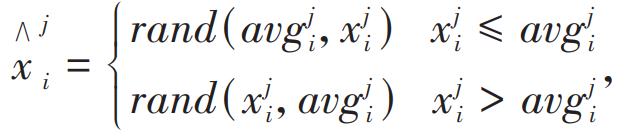
In the equation, xji represents the position of the i-th whale in the jth dimensional space; Aji and bji are the lower and upper boundaries of xji, respectively.
The convergence factor a (t) varies linearly and cannot adapt to the nonlinear change process during the update iteration process. A nonlinear convergence factor is introduced to fully explore its global search and local development capabilities, namely:
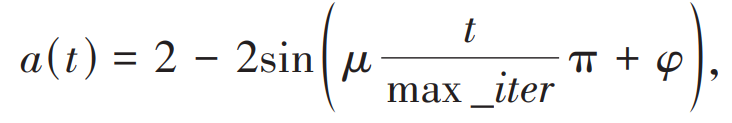
In the equation: μ and φ Respectively represent their relevant parameters, and select μ = 0.5, φ = 0
To avoid the phenomenon of whale algorithm falling into local optima and premature convergence, an adaptive weight strategy and a random difference strategy are proposed to ensure population diversity and achieve global optimization. The adaptive weight strategy is shown in equation (26), and the random difference strategy is:
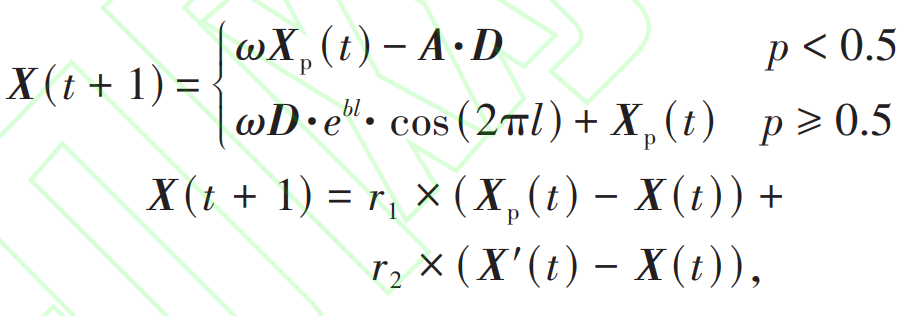
In the formula, X ‘(t) is the position vector of random individuals in the population.
3.3 Shared energy storage optimization configuration
The established shared energy storage optimization configuration model adopts improved WOA solution, and the specific process is as follows.
(1) Input system data such as new energy generation power, grid connected power demand, and price, initialize and improve parameters such as WOA population size, maximum iteration times, and spiral coefficient.
(2) Initialize population individuals using quasi reverse learning in the solution space.
(3) When the number of iterations is less than the maximum number of iterations, calculate the optimal individual position and fitness function values and record them.
(4) Update the bounding stage model using nonlinear factors to improve global search and local development capabilities.
(5) Using adaptive strategy and random difference mutation strategy to update the optimal position of the population, the number of iterations is increased by 1.
(6) When the iteration termination judgment condition is met, the optimal individual positions and fitness function values are output.
(7) Obtain the optimized configuration results, charging and discharging power, and status of shared energy storage power plants.
4 Example analysis
4.1 Example Setting
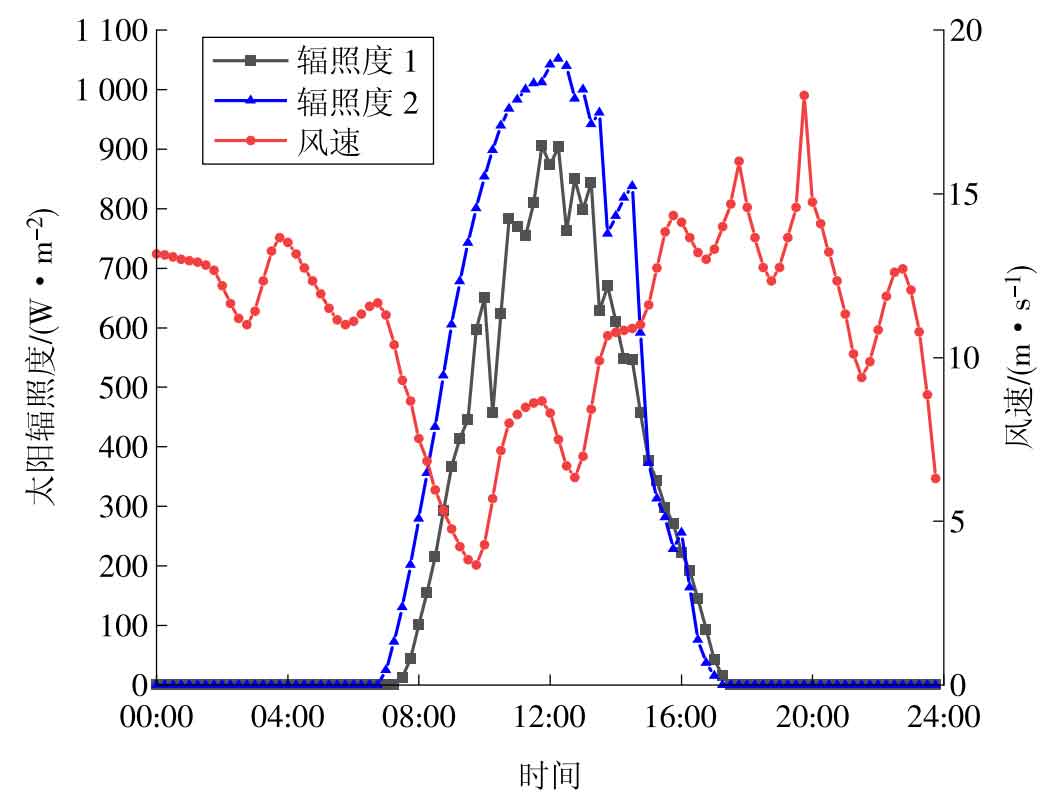
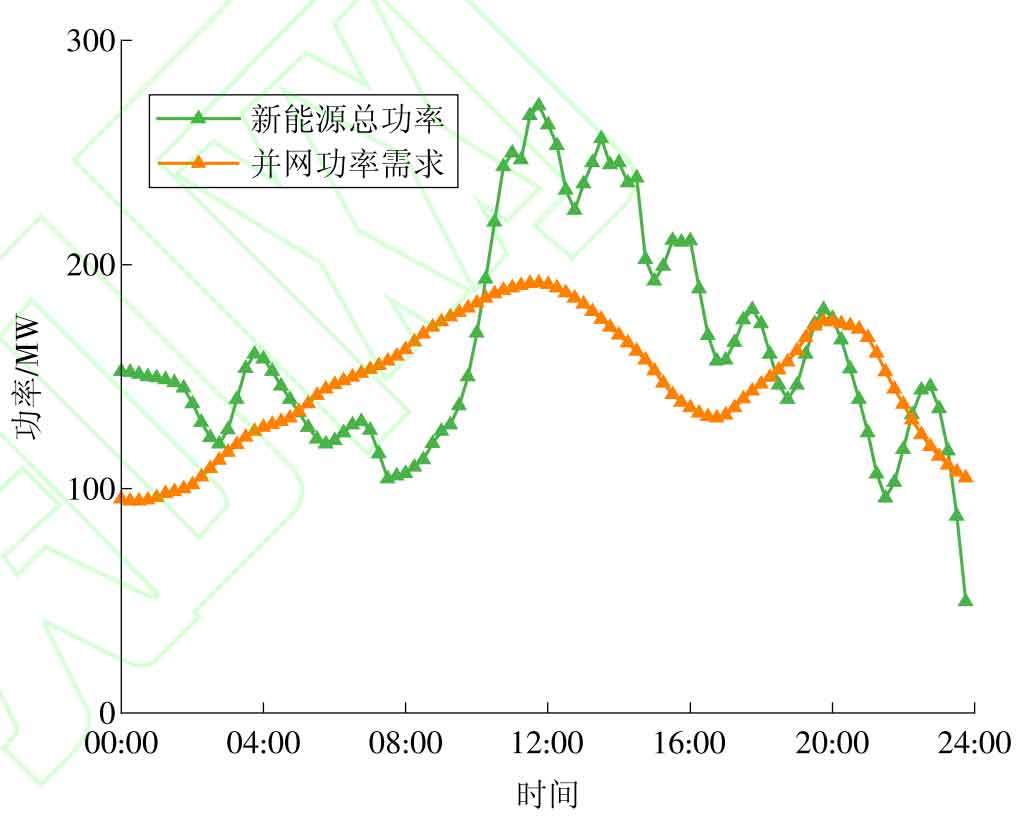
To verify the feasibility of the optimized configuration model in this article, two photovoltaic power plants with an installed capacity of 100 MW and one wind farm with an installed capacity of 180 MW were selected from a certain region in northwest China to configure shared energy storage for these three new energy power plants. Based on the analysis of typical daily new energy output and grid connection demand, the parameters of centralized shared energy storage are shown in Table 1. According to the annual observation data of new energy stations, typical daily wind speed and solar irradiance are shown in Figure 2. Combining typical daily wind speed and solar irradiance, the total power and grid connected power requirements of the new energy station are shown in Figure 3.
| Parameter | Value |
| Unit power investment cost cP/(10000 yuan · MW ^ -1) | 40 |
| Unit capacity investment cost cE/(10000 yuan · (MW · h) ^ -1) | 70 |
| Benchmark discount rate r/% | 0.5 |
| Shared energy storage power plant operating life n/a | 10 |
| Operation and maintenance coefficient of shared energy storage power station ζ/% | 6 |
| Charging and discharging efficiency η ESS, c, η ESS, d | 0.95 |
Centralized shared energy storage is beneficial for improving the utilization rate of energy storage resources and reducing the investment cost of energy storage. To better compare the impact of energy storage on new energy consumption in different scenarios, the following three scenarios are set up.
Scenario 1: Each new energy station is not equipped with energy storage;
Scenario 2: Each new energy station is equipped with independent energy storage;
Scenario 3: New energy stations are equipped with centralized shared energy storage.
4.2 Result analysis
4.2 1 Scenario 1 Result Analysis
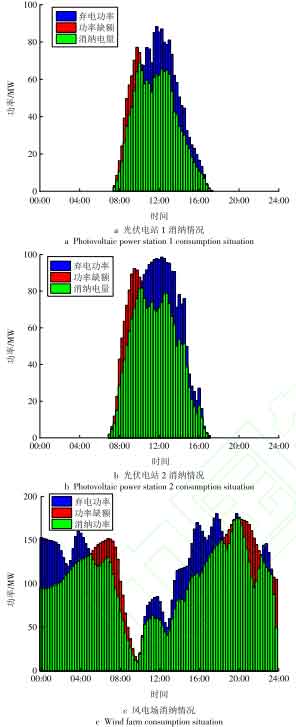
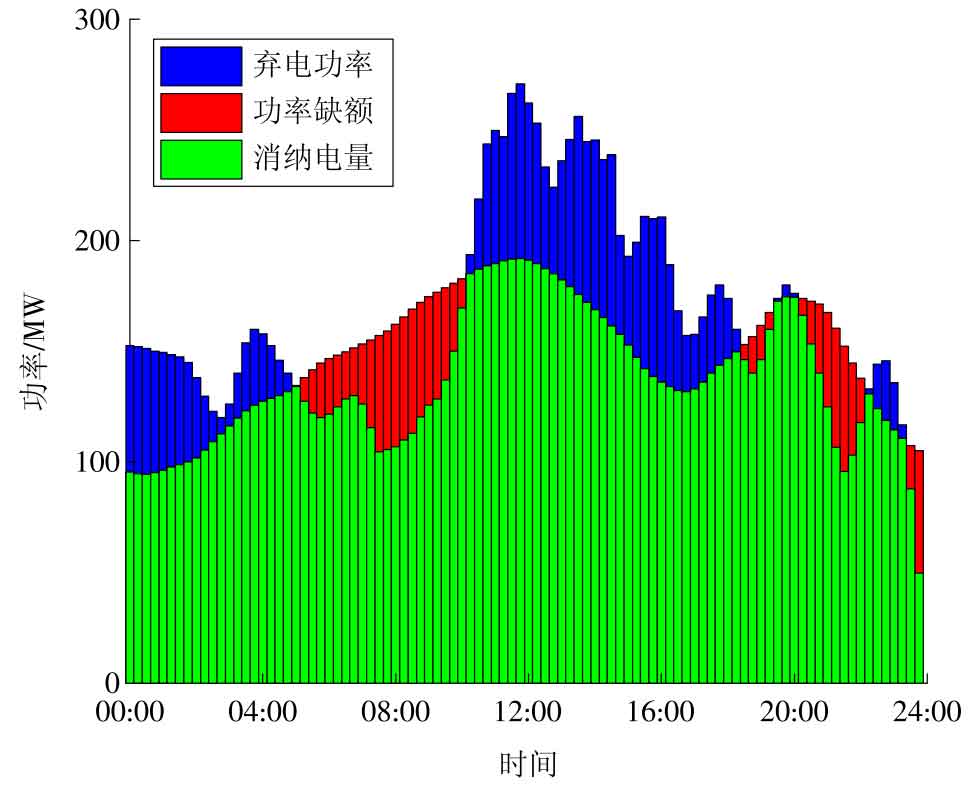
Due to the randomness and volatility of wind and photovoltaic power generation, new energy generation may encounter situations where the output on the generation side cannot match the grid connection demand and be fully absorbed. When the output of new energy is surplus, a large amount of electrical energy is wasted due to its inability to be utilized; When the output of new energy is insufficient, it will create a shortage of success rates, making it difficult to meet the grid connected power demand. The actual output and consumption situation of each new energy power station is shown in Figure 4, while the total output of new energy, grid connection demand, grid connection power shortage, consumption and abandonment situation are shown in Figure 5.
To intuitively reflect the actual consumption of new energy, the calculation formula for the new energy consumption rate is:
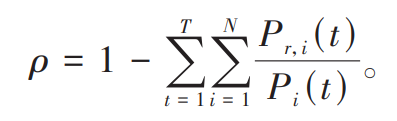
By analyzing Figures 4 and 5, using equation (28), the new energy consumption rate is calculated to be 84 08% of the remaining electricity is wasted due to the inability to store and utilize it, resulting in low economic efficiency of new energy, which is not conducive to the development of new energy. At the same time, there is a power shortage phenomenon that threatens the stable operation of the power grid. Analyzing and comparing the actual and total consumption of new energy at various stations, it is found that wind power and photovoltaic power have complementary characteristics in terms of time, reducing the waste of new energy. Abandonment of electricity is mainly concentrated during the time periods of 00:00-04:00 and 10:00-18:00, during which the wind and photovoltaic power generation is greater than the grid consumption. During the time periods of 04:00-10:00 and 20:00-22:00, the demand for grid connected power was greater than the actual power generated by the new energy station, resulting in the inability of the new energy output to meet the grid connected power demand, resulting in a shortage of grid connected power.
4.2.2 Scenario 2 Result Analysis
The output of each new energy station has volatility, and the new energy absorption capacity is insufficient. Energy storage can be used to suppress random fluctuations in power and improve the new energy absorption capacity. According to the existing energy storage configuration requirements of new energy stations, the energy storage power is configured at 15% of the installed capacity of the new energy stations. In order to better compare and analyze with Scenario 3, the energy storage duration in this scenario is set to 6 hours, which means that each new energy station is equipped with independent energy storage, as shown in Table 2. The photovoltaic power stations are equipped with independent energy storage of 15MW/90 MW · h, and the investment and construction cost is 631 790000 yuan/a, the wind farm is equipped with independent energy storage of 27 MW/162 MW · h, and the investment and construction cost is 1137 220000 yuan/a, which means the total installed capacity of independent energy storage is 57MW/342 MW · h, with a total investment and construction cost of 2400 yuan 800000 yuan/a. The consumption situation of each new energy station after configuring independent energy storage is shown in Figure 6, and the total consumption situation of the new energy station after configuring independent energy storage is shown in Figure 7.
| Type | Power/MW | Capacity (/MW · h) | Configuration cost/(10000 yuan · a ^ -1) |
| Photovoltaic power station 1 | 15 | 90 | 631.79 |
| Photovoltaic power station 2 | 15 | 90 | 631.79 |
| Wind farm | 27 | 162 | 1137.22 |
| Total | 57 | 342 | 2400.80 |
Figures 6 and 7 reflect the independent energy storage configuration of new energy stations, which stores electricity when the power generated exceeds the grid connected power demand and releases electricity when there is a power shortage. By analyzing the independent energy storage and consumption situation of the new energy station configuration, according to equation (28), the new energy consumption rate is calculated to be 92 7%. Independent energy storage plays an important role in improving the consumption rate of new energy and reducing the shortage of grid connected power, but independent energy storage has a lower efficiency in the consumption and utilization of new energy. Among them, the energy storage system of photovoltaic power plants only achieves one charging and discharging process, and is mostly idle; The energy storage system of a wind farm may undergo multiple charging and discharging processes, but due to the limited power and capacity of the configured energy storage system, it is unable to fully absorb excess energy and compensate for power shortages.
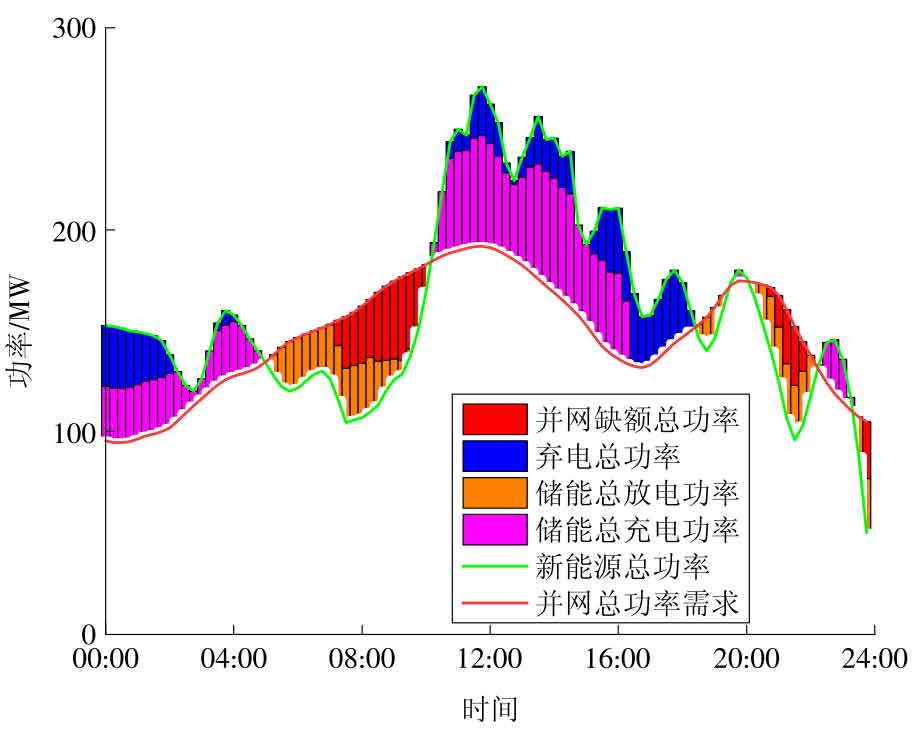
4.2 3 Scenario 3 Result Analysis
According to the demand for new energy generation power and grid connected power, the optimized configuration of shared energy storage for consumption towards new energy stations is shown in Table 3. Figure 8 shows the new energy consumption rate and shared energy storage configuration power
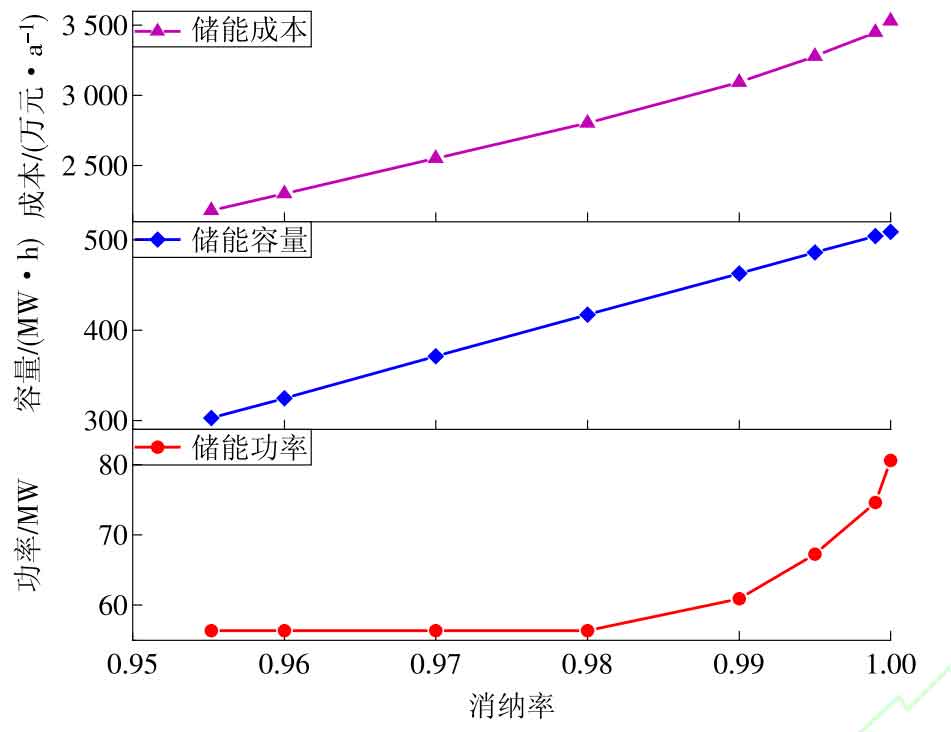
| Number | Power/MW | Capacity/(MW · h) | Energy storage ratio/% | Consumption rate/% | Configuration cost/(10000 yuan · a ^ -1) |
| 1 | 56.37 | 302.54 | 14.83 | 95.52 | 2180.35 |
| 2 | 56.37 | 324.64 | 14.83 | 95.00 | 2300.44 |
| 3 | 56.37 | 370.85 | 14.83 | 97.00 | 2551.59 |
| 4 | 56.37 | 417.06 | 14.83 | 98.00 | 2802.73 |
| 5 | 60.94 | 462.70 | 16.04 | 99.00 | 3094.20 |
| 6 | 80.59 | 508.91 | 21.21 | 100.00 | 3532.30 |
Capacity and cost relationship curve. From Table 3 and Figure 8, it can be seen that as the energy storage capacity and power increase, the energy storage cost increases and the new energy consumption rate also improves. Meanwhile, Figure 8 reflects that under the same energy storage power, the energy storage capacity will affect the new energy consumption rate. In the process of optimizing energy storage configuration, the impact of energy storage capacity on configuration cost is greater than the impact of energy storage power. From the perspective of shared energy storage economy, the initial investment and construction cost of shared energy storage is huge, and the increase in new energy consumption rate will lead to an increase in energy storage configuration costs, which is not conducive to the development of shared energy storage.
In summary, selecting a reasonable return on energy storage investment and new energy consumption rate is a prerequisite for optimizing the allocation of shared energy storage, with the goal of maximizing economic benefits. Therefore, Scheme 1 is selected as the research object. The shared energy storage configuration has a power of 56 37 MW, with a configured capacity of 302 54 MW · h, the new energy consumption rate calculated according to equation (28) is 95 52%. By calculating the cost of shared energy storage configuration, it is 2180 350000 yuan/a, based on market electricity prices and energy storage service prices, a shared energy storage investment return rate of 20 80%.

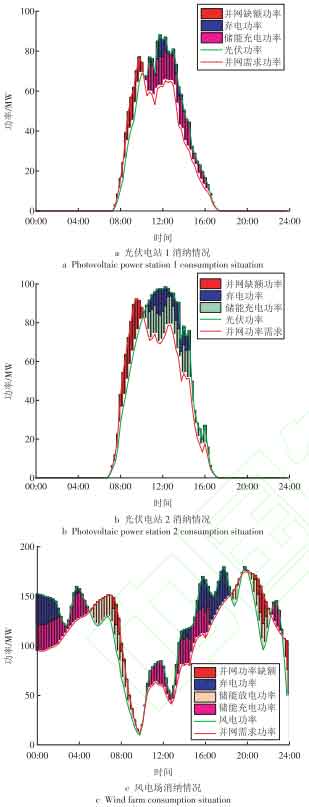
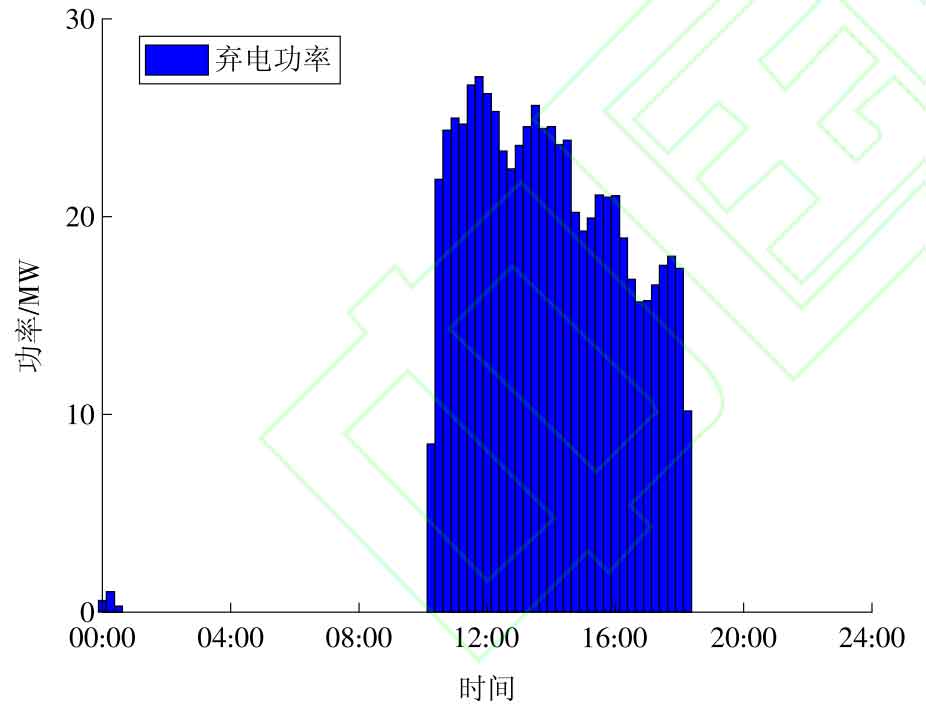
Under the action of shared energy storage power stations, the power of new energy waste is shown in Figure 9. From the perspective of new energy consumption, both photovoltaic power plants and wind farms have experienced varying degrees of power abandonment, but the time periods for power abandonment are basically overlapping, concentrated between 10:00-18:00. The main reason is that the total output of wind and solar power is greater than the sum of the grid connected load demand and the maximum energy storage consumption power, leading to partial energy waste. From the perspective of grid connected power, under the role of shared energy storage, the grid connected power shortage caused by insufficient output of new energy is compensated, ensuring the dynamic balance between grid connected power demand and power supply side, which is conducive to improving the stability of grid operation. The improvement of new energy consumption capacity is attributed to the participation of shared energy storage. In order to better demonstrate the actual operation status of shared energy storage, from an operational perspective, the power, state, and SOC variation curves of typical daily participation in shared energy storage power stations for each new energy station are shown in Figure 10. The power changes of shared energy storage participating in new energy consumption and grid connected power support are shown in Figure 11. The trend of SOC changes in shared energy storage power plants is influenced by the charging and discharging status of energy storage, which depends on the new energy generation power and grid connected power demand. The idle time of shared energy storage for new energy consumption scenarios has been significantly reduced, and the fluctuation frequency of new energy output will affect the charging and discharging frequency of energy storage.

4.2 4. Comparative analysis of calculation examples
According to the comparative analysis of three scenarios for new energy consumption, Scenario 1 shows that the new energy station group includes wind power and photovoltaic power generation, which are complementary in terms of time. However, the lack of energy storage in each station will result in a large amount of energy being unusable and wasted, leading to severe power shortages in grid connected power demand. At the same time, the output of new energy is stochastic and periodic, resulting in certain resistance to grid connected operation of new energy stations. Scenario 2: The new energy station suppresses output fluctuations by configuring independent energy storage. When the output exceeds the grid connected power demand, the energy storage acts as a load to consume excess electricity. When there is a power gap between output and grid connected power, the energy storage system releases electricity to compensate for the power gap. The addition of independent energy storage improves the new energy consumption rate and reduces the power gap in Scenario 2 based on Scenario 1, but the energy storage utilization rate is relatively low, Limited ability to absorb excess electricity. For the scenario of new energy consumption, Scenario 3 promotes new energy consumption through centralized shared energy storage on the power generation side, and optimizes the configuration with the goal of maximizing the economic benefits of shared energy storage. The results show that shared energy storage has a positive effect on new energy consumption and compensating for power shortages. At the same time, on the basis of Scenario 2, it significantly reduces the power difference between new energy output and grid connected power demand, improving the stability of the power grid, At the same time, it reduces the idle time of energy storage and improves the utilization rate of energy storage.
Comparing Scenario 2 with Scenario 1, it can be seen that configuring independent energy storage at new energy stations is beneficial for improving the new energy consumption capacity. After configuring independent energy storage, the new energy consumption rate has increased by 8. 5% 62%, also reducing the shortage of grid connected power; Comparing Scenario 3 with Scenario 2, it can be seen that shared energy storage can avoid the current situation of limited independent energy storage regulation capacity, while reducing the idle time of energy storage and improving the utilization rate of energy storage resources. In terms of new energy consumption, due to the huge investment cost of energy storage, the selected shared energy storage configuration scheme has increased the energy storage consumption capacity by 2. 5% compared to independent energy storage under the same investment situation 82%, the profit model of shared energy storage also shortens the payback period of energy storage investment, which helps to promote the development of the shared energy storage operation model.
5 Conclusion
In order to improve the serious waste of energy storage resources, lack of business models, and long investment payback period in new energy consumption scenarios, a shared energy storage optimization configuration model with the goal of maximizing shared energy storage revenue is proposed, taking into account the constraints of new energy consumption, energy storage power stations, and the demand for energy storage charging and discharging from new energy stations. The improved WOA is used to solve the problem. By comparing and analyzing the participation level of energy storage in new energy consumption scenarios, the following conclusions can be drawn.
(1) The configuration of shared energy storage in new energy stations can further improve the absorption capacity of new energy, suppress output fluctuations, and help reduce grid connected power shortages. The centralized shared energy storage mode on the power generation side can fully utilize energy storage resources, maximize the time-shift characteristics of energy storage, absorb surplus energy, and compensate for power shortages, effectively leveraging the complementary and regulatory characteristics between wind and solar energy storage.
(2) The operating mode of shared energy storage has broken the dilemma of single independent energy storage service objects and limited consumption and regulation capabilities. By sharing energy storage resources, the economic value of mining energy storage resources is fully realized, with an investment return rate of 20 8%, effectively shortening the payback period of energy storage investment.
(3) The economy of shared energy storage is closely related to the consumption rate of new energy. When the power of energy storage configuration is the same, the consumption rate directly affects the capacity of energy storage configuration, leading to a sharp increase in investment and construction costs, extending the return period of energy storage investment, and is not conducive to the development of shared energy storage.
