With the transformation of the global energy structure, the “dual carbon” goal continues to deepen, and clean energy represented by wind power has achieved rapid development. As of 2022, China’s wind power grid connected total installed capacity has ranked first in the world for 13 consecutive years, with a cumulative installed capacity exceeding 350 million kW. However, the random changes in wind speed result in strong fluctuations in wind power generation power, seriously threatening the safe operation of a high proportion of new energy power systems. As an important flexible resource supporting the high proportion consumption of new energy, the four quadrant operating characteristics of energy storage can effectively suppress the fluctuating power of wind power and alleviate the impact of strong uncertainty on the power system.
In recent years, the use of energy storage to suppress fluctuations in renewable energy has been widely studied. Common methods include fuzzy control, low-pass filtering, empirical mode decomposition, model predictive control (MPC), uncertainty optimization, and so on. Adopting fuzzy control technology to dynamically optimize the power allocation of hybrid energy storage systems, achieving effective suppression of wind farm power fluctuations. A smooth control strategy for multi type energy storage systems is proposed by combining real-time wavelet transform with double-layer fuzzy control methods. Utilize energy storage to suppress the momentum of wind waves in a specific frequency band, while dynamically adjusting the filtering time constant based on the battery’s state of charge. The improved set empirical mode decomposition and grey correlation degree are used to decompose the power generation of new energy sources, thereby obtaining the power allocation results of hybrid energy storage. A hybrid energy storage control strategy based on Hilbert Huang transform and model predictive control was proposed. A two-layer stochastic model predictive control method considering wind power uncertainty is proposed, which achieves smoothing of wind power fluctuations through rolling optimization of energy storage output. A stochastic model predictive control strategy for wind storage joint systems is proposed by quantifying wind power uncertainty using conditional constraints of probability prediction. The uncertainty of wind power is mainly manifested in fuzziness and randomness, and its prediction errors exhibit characteristics such as asymmetry and heteroscedasticity.
However, commonly used deterministic prediction methods such as point prediction often assume that the prediction error follows a normal distribution, which reduces the accuracy of wind power prediction. Therefore, the output of the energy storage system obtained is also inaccurate. To improve the output characteristics of wind power generation, this paper proposes a robust model predictive control technology for wind storage systems aimed at power suppression. The uncertainty of wind power generation is described through a box uncertainty set. Firstly, a two-layer robust optimization model for the wind storage system is established based on this. The established robust optimization model ensures that the wind storage joint system can meet power fluctuation constraints in any wind power output scenario. Secondly, based on the strong duality theory, the double-layer robust optimization model of the wind storage system is transformed into a single-layer deterministic optimization model, significantly improving the solving efficiency and quality of the model. The bilinear constraints in the model were transformed into a set of linear inequality constraints using the large M method, achieving linearization of non convex constraints. Finally, an evaluation index for the smoothing effect of wind power fluctuations, including the mean value of grid connected power fluctuations, was established, and the advantages of the proposed method in terms of smoothing effect and operational economy were verified through numerical examples.
1.Grid connected model of wind storage system
1.1 Power model of wind storage system
The random changes in wind speed result in strong fluctuations in wind power generation power, seriously threatening the safe operation of a high proportion of new energy power systems. Energy storage has the characteristic of flexible operation in four quadrants. By designing a reasonable energy storage charging and discharging strategy, it can cooperate with wind power generation systems to achieve smooth and stable power output.
The power output of the wind storage system is the sum of the outputs of the wind farm and the energy storage plant, expressed as:
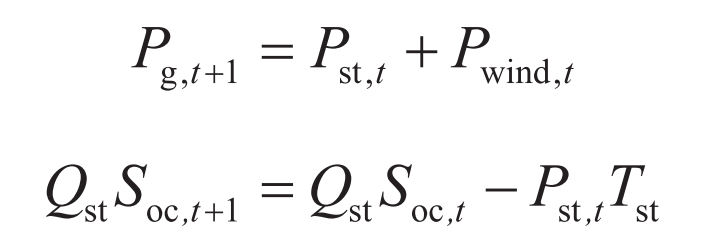
In the formula: Pg, t+1 is the grid connected power of the wind storage system at time t+1; Pst, t is the output power of the energy storage station at time t; Pwind, t is the output power of wind power generation at time t; Qst is the capacity of the energy storage power station; Soc, t is the state of charge of the battery at time t; Tst is the control cycle of the energy storage plant. The output of wind power is uncontrollable, and the maximum fluctuation in grid connected power of the wind storage joint system is ε, The output power of the joint system at time t+1 should be within [Pg, t- ε, Pg, t+ ε] Within the scope. If the wind power output at time t+1 is higher than Pg, t+ ε Or lower than Pg, t- ε, It is necessary to control the charging and discharging of energy storage to meet the output power requirements of the joint system.
1.2 Wind Power Uncertainty Modeling
Traditional wind power prediction methods such as point prediction usually assume that the wind power prediction error follows a specific distribution such as normal, in order to obtain deterministic wind power output prediction results and determine the charging and discharging strategies for energy storage based on it. To avoid parameterized assumptions of wind power prediction errors, this article uses a box uncertainty set to model wind power output Pwind, t:
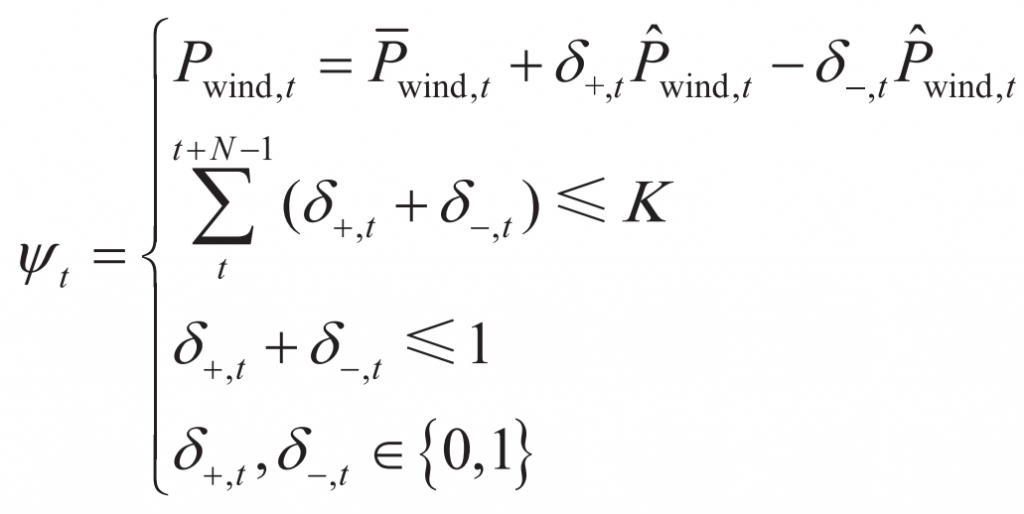
In the formula: is the predicted power output of the wind farm; The maximum allowable prediction error for the output power of the wind farm; K is the time sequence of the fluctuation of stroke electricity in the predicted interval; N is the lead time for wind power prediction; δ+, T δ-, Both t are binary variables of the predicted wind power error.
1.3 Power fluctuation evaluation indicators
In order to more intuitively evaluate the smoothing effect of wind power grid connected power curve, the mean fluctuation of grid connected power ∆ Pg was defined_ Mean, the total energy of charging and discharging during the operation of the energy storage power plant, Est_ Total, and the output coefficient Cst of the energy storage plant_ CO as an evaluation indicator.
Mean fluctuation of grid connected power ∆ Pg_ Mean is used to evaluate the fluctuation level of wind power after stabilization. The smaller the value, the smoother the output of the wind storage system and the better the stabilization effect.
In the formula: ∆ Pwind, t is the absolute value of the grid connected power fluctuation of the wind storage system.
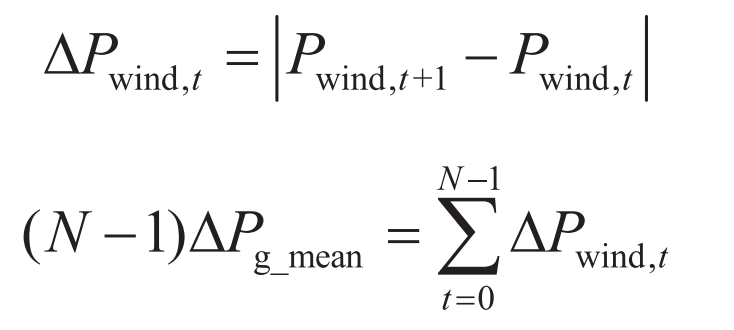
The total energy of charging and discharging during the operation of energy storage power plants, Est_ Total is used to quantify the energy exchange volume of energy storage stations participating in wind power fluctuation mitigation.
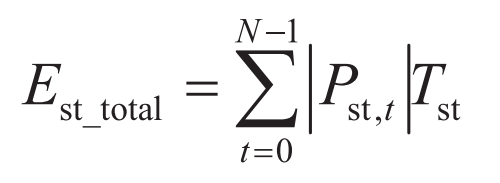
Output coefficient Cst of energy storage power station_ The size of co characterizes the output capacity of energy storage power plants, Cst_ The smaller the value of co, the greater the power output capacity of energy storage.
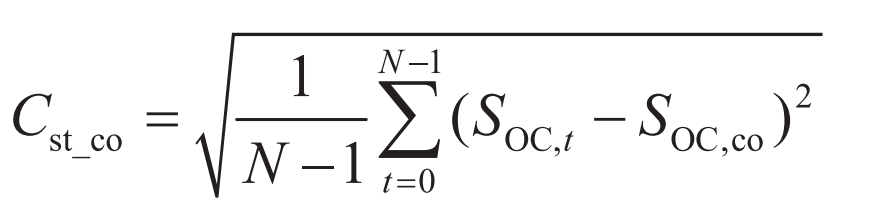
In the formula, SOC and co are the optimal power output states for energy storage, and their values can usually be selected as 0.5.
2.Robust Model Predictive Control
2.1 Objective function
Robust optimization aims to ensure that the obtained solution meets any uncertainty condition, and can fully cope with all uncertainty risks. Therefore, it is widely used in uncertainty optimization of power systems. This article adopts robust optimization algorithms to ensure that the charging and discharging strategies of energy storage plants can meet the suppression requirements of any operating conditions of wind farms. In the optimization period t, the objective function of robust model predictive control is expressed as:
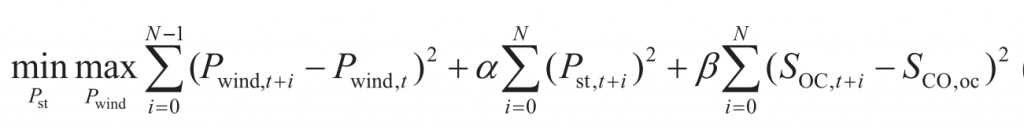
In the equation: α、β All are weight coefficients of control objectives.
2.2 Constraints
In addition, the power output of the wind storage system should meet the grid connection conditions, that is, the fluctuation value of the grid connection power should be less than ε:
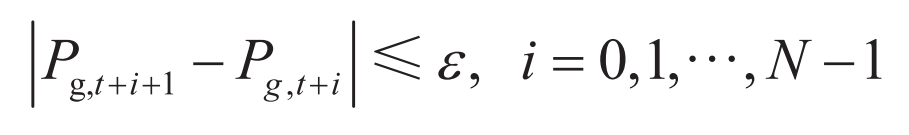
The state of charge of batteries in energy storage power stations can be calculated using the following equation:
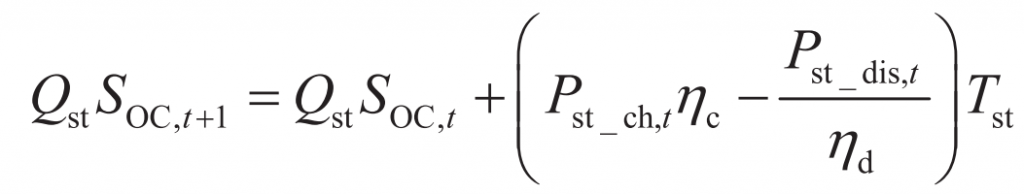
In the equation: Pst_ Ch, t, Pst_ Dis, t are the charging and discharging power of the battery in the energy storage station; η C η D represents the charging and discharging efficiency of energy storage.
Energy storage stations cannot simultaneously execute charging or discharging commands, therefore the following constraints must be met:
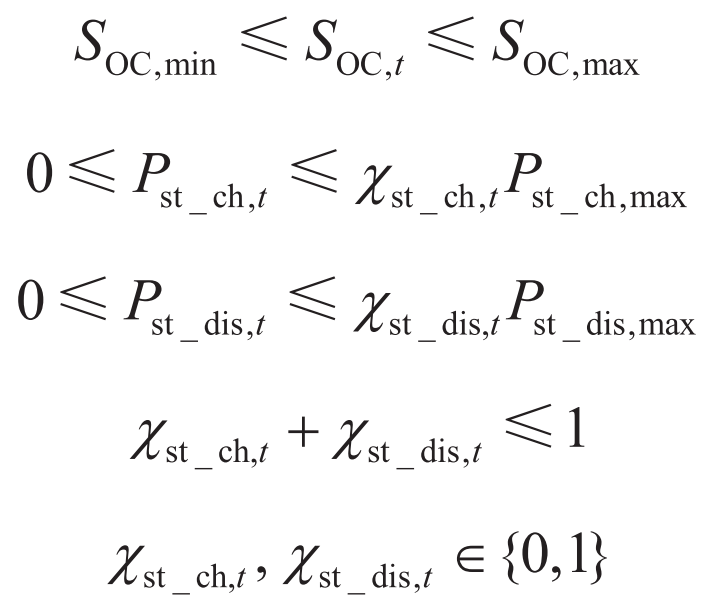
In the formula: Soc, min, Soc, max are the minimum and maximum state of charge of the energy storage power station, respectively; Pst_ Dis, max, Pst_ Ch, max are the maximum discharge and charging power of the energy storage station, respectively; χ St_ Ch, t χ St_ Dis and t are binary variables that represent the charging and discharging operation status of the power plant, χ St_ Ch, t=1 indicates that the energy storage station is in a charging state, χ St_ Dis, t=1 indicates that the energy storage plant is in a discharge state.
3.Model solving method
3.1 Determination Method for Uncertainty Models Based on Strong Dual Theory
The robust model predictive control model for wind storage systems facing power suppression can be expressed as:
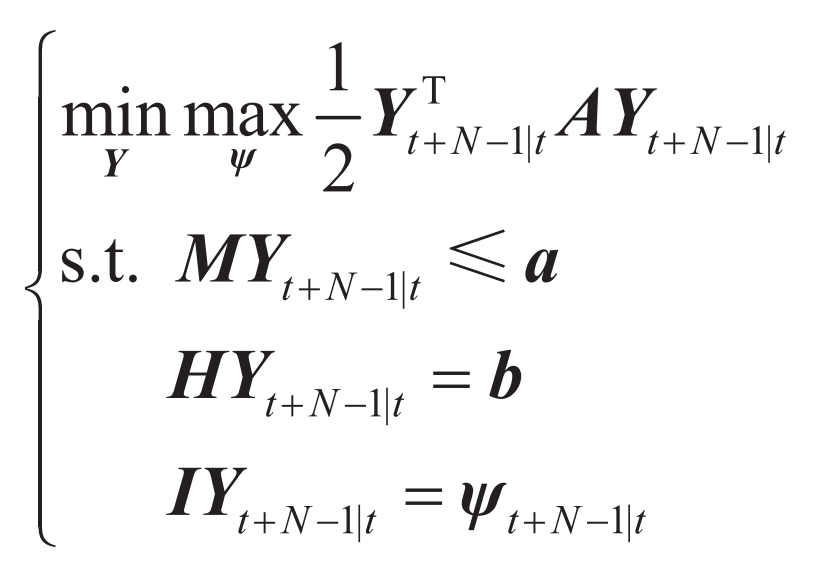
In the formula: A is a positive definite matrix; Yt+N-1 | t is the decision variable obtained by advancing multiple time series; M. H and I are constant matrices; a. B is a constant vector.
It can be seen that the model equation (17) contains both inequality constraints and equality constraints, where the constraint IYt+N-1 | t= Ψ T+N-1 | t also includes uncertain variables.
Due to the inclusion of uncertain variables in the above model, it is not possible to solve it using mature solvers such as Cplex/Urobi. Therefore, the dual method is used to transform the original double-layer model into a single-layer deterministic optimization model:
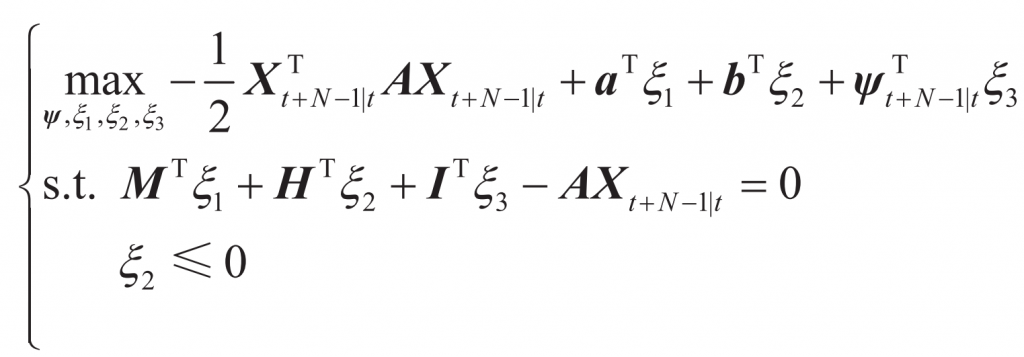
In the formula: Xt+N-1 | t is the dual variable of Y; ξ 1 ξ 2 and ξ All 3 are dual variables. By combining the above single-layer deterministic optimization model [Equation (18)] with the uncertainty set [Equation (3)], a dual model of the original optimization problem can be obtained, but the model contains nonlinear bilinear terms. Therefore, based on the large M method, replacing bilinear terms with a series of linear inequality constraints can obtain:
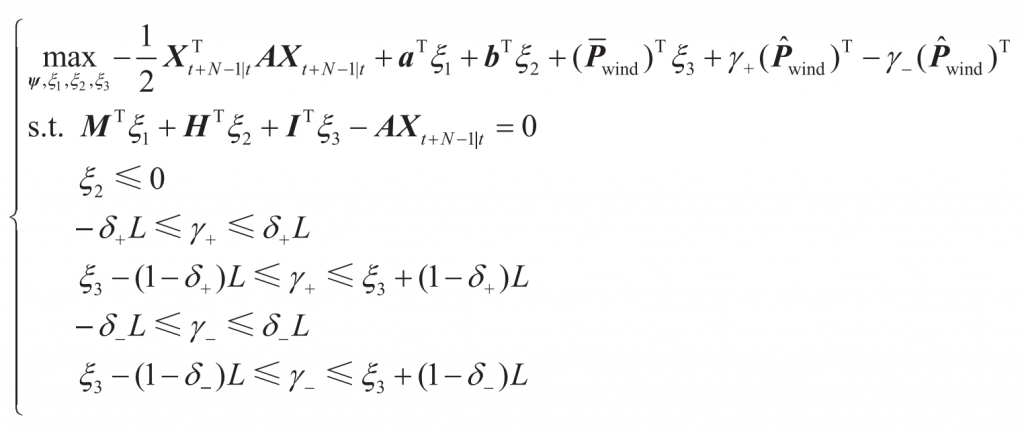
In the formula: is the predicted power output of the wind farm; The maximum allowable prediction error for the output power of the wind farm; γ+ and γ- All are auxiliary variables, where γ+=δ+ξ 3T, γ-=δ-ξ 3T; L is a large number introduced by the Big M method.
3.2 Control Strategy Process
Wind power prediction errors can affect the effectiveness of wind power fluctuation suppression technology. Based on robust model predictive control, this paper proposes a wind power fluctuation suppression technology that considers wind power prediction errors. Figure 1 shows the process of suppressing wind power fluctuations based on robust model predictive control.
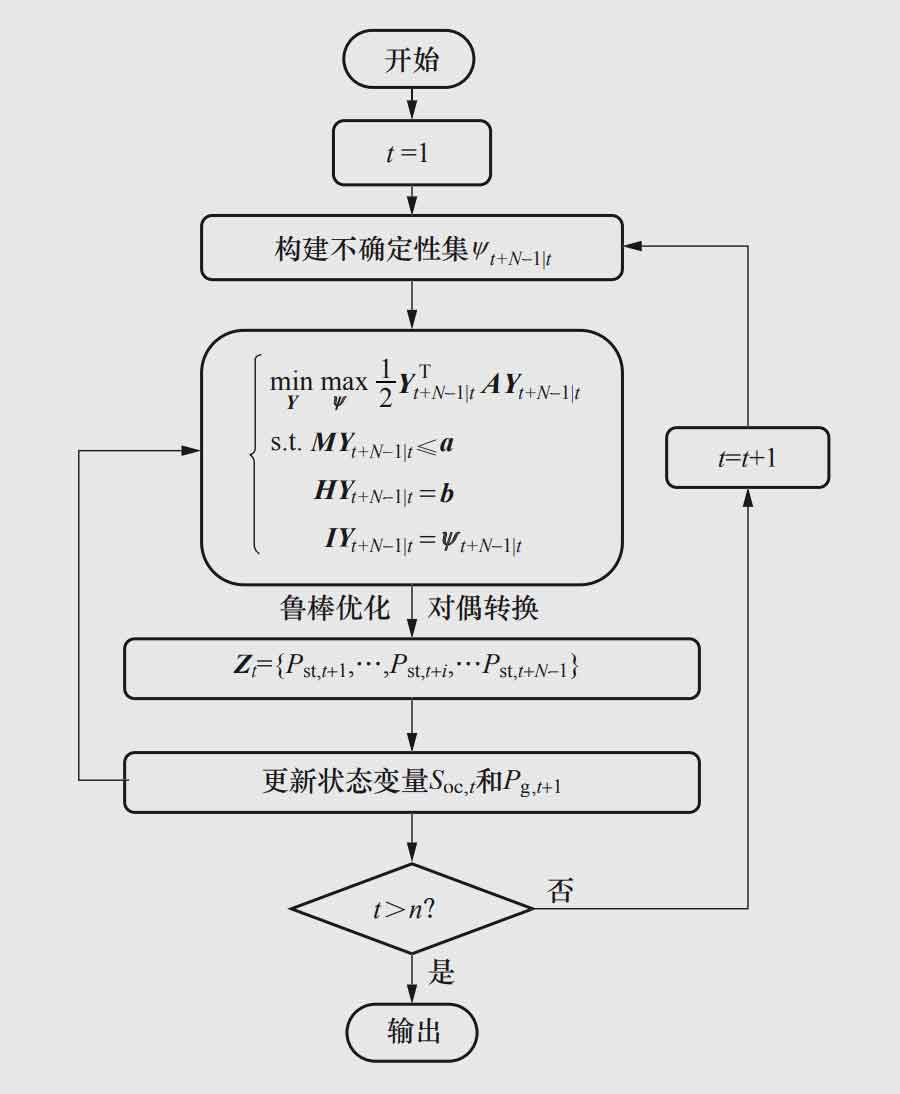
The specific steps of the process are as follows:
Step 1: Construct a wind power uncertainty set based on the wind power prediction sequence Ψ T+N-1 | t;
Step 2: Establish a robust model predictive control model for wind storage systems aimed at power suppression, and use a dual method to transform the original double-layer uncertainty model into a single-layer model;
Step 3: Solve and calculate the optimal output time series Zt={Pst, t+1,…, Pst, t+i,…, Pst, t+N-1} for the future predicted time domain N at time t;
Step 4: Input the first value Pst, t+1 of the optimal output sequence Zt of the energy storage system into the wind storage system, calculate the state variables SOC, t+1, Pg, t+1, and establish an operational optimization model for the next time series based on this;
Step 5: If the number of optimizations exceeds the set maximum number of optimizations n, stop scrolling, otherwise proceed to step 1 again.
4.Example analysis
4.1 Example parameters
The example uses the actual wind power output of a 100 MW wind farm in China for 10 consecutive days in summer to verify the effectiveness of the proposed method. The data resolution is 15 minutes, the allowable grid connected power fluctuation is 10 MW, and the maximum error of wind power prediction is 10%. The power and capacity of the energy storage station are 25 MW/50 MWh, with a control period of 15 minutes. The upper and lower limits of the battery state of charge are 0.8 and 0.2, respectively. The model predicts a rolling optimization time domain length of 4 hours.
4.2 Analysis of Wind Power Fluctuation Suppression Effect
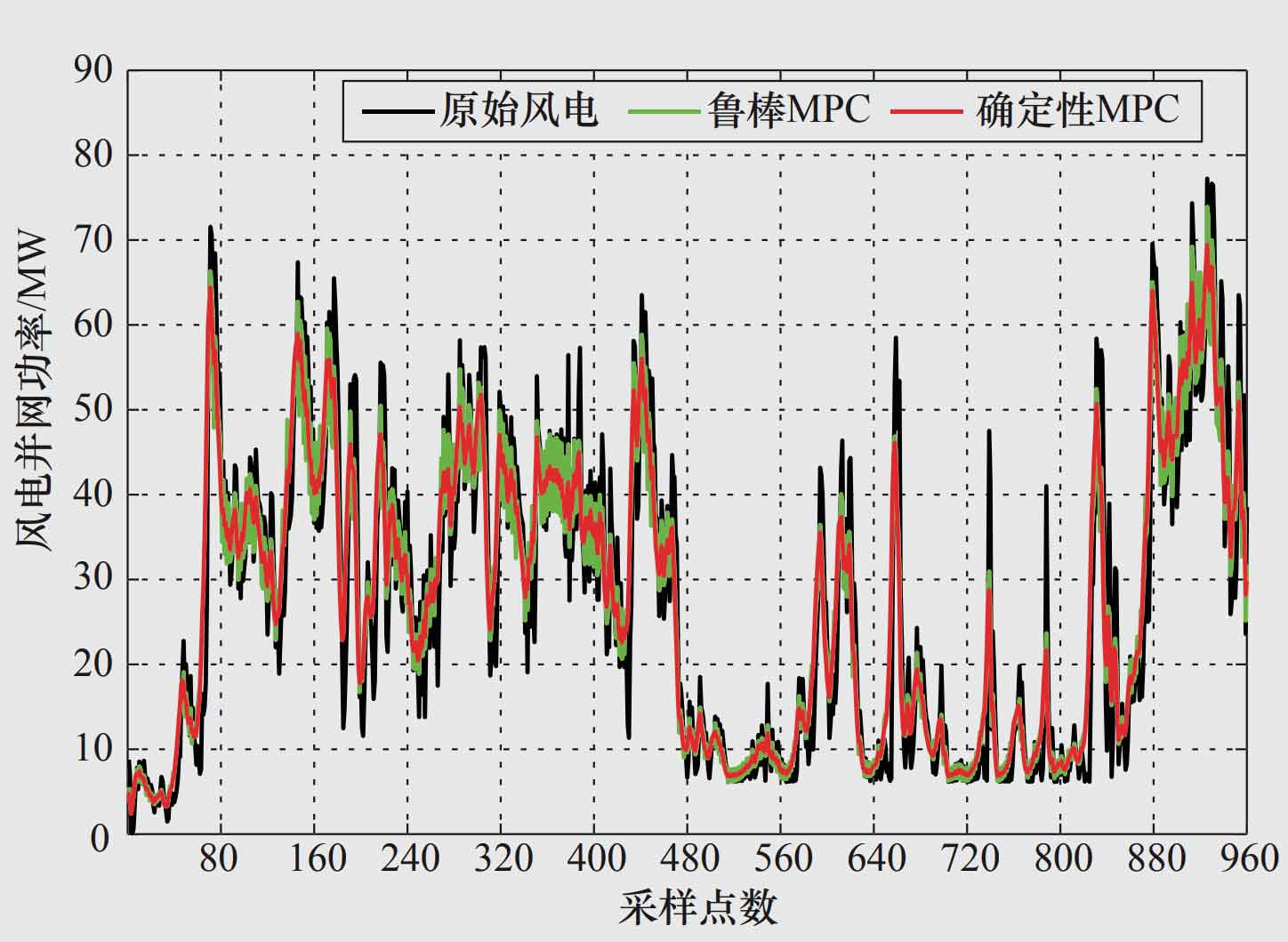
Figure 2 shows the wind power grid connected power curve after using two methods, deterministic MPC and robust MPC, to suppress wind power fluctuations. It can be seen that the application of both methods has improved wind power grid connected power fluctuations to varying degrees, but compared to the deterministic MPC method, robust MPC has better suppression effect. Table 1 presents the comparison results of the mean fluctuation of grid connected power after smoothing using three methods: robust MPC, first-order low-pass filtering, and deterministic MPC. It can be seen that the first-order low-pass filtering method has the worst fluctuation smoothing effect. The mean absolute value of grid connected power fluctuation after using deterministic MPC method to suppress is 2.749 3, while the mean absolute value of grid connected power fluctuation obtained using robust MPC method is only 1.566 8. Due to the robust MPC considering the prediction error of wind power and adjusting the output of energy storage plants in real-time based on this, the suppression of actual wind power fluctuations is more sufficient.
| Control methods | Original wind power | First order low-pass filtering | Deterministic MPC | Robust MPC |
| ∆Pg_mean/MW | 4.373 3 | 3.129 7 | 2.7 49 3 | 1.566 8 |
Table 2 presents the comparison results of the total energy of charge and discharge for three methods: robust MPC, first-order low-pass filtering, and deterministic MPC. It can be seen that compared to the low-pass filtering method, the total energy Est of charge and discharge for energy storage plants using robust MPC method_ The total reduction of 255.4 MWh indicates that the robust MPC smoothing method has better economy. Compared to deterministic MPC, the total energy Est of charging and discharging for energy storage plants with robust MPC_ Total increased by 173.7 MWh as robust MPC requires more energy storage to cope with wind power uncertainty.
| Control methods | First order low-pass filtering | Deterministic MPC | Robust MPC |
| Est_total/MWh | 1 272.8 | 843.7 | 1017.4 |
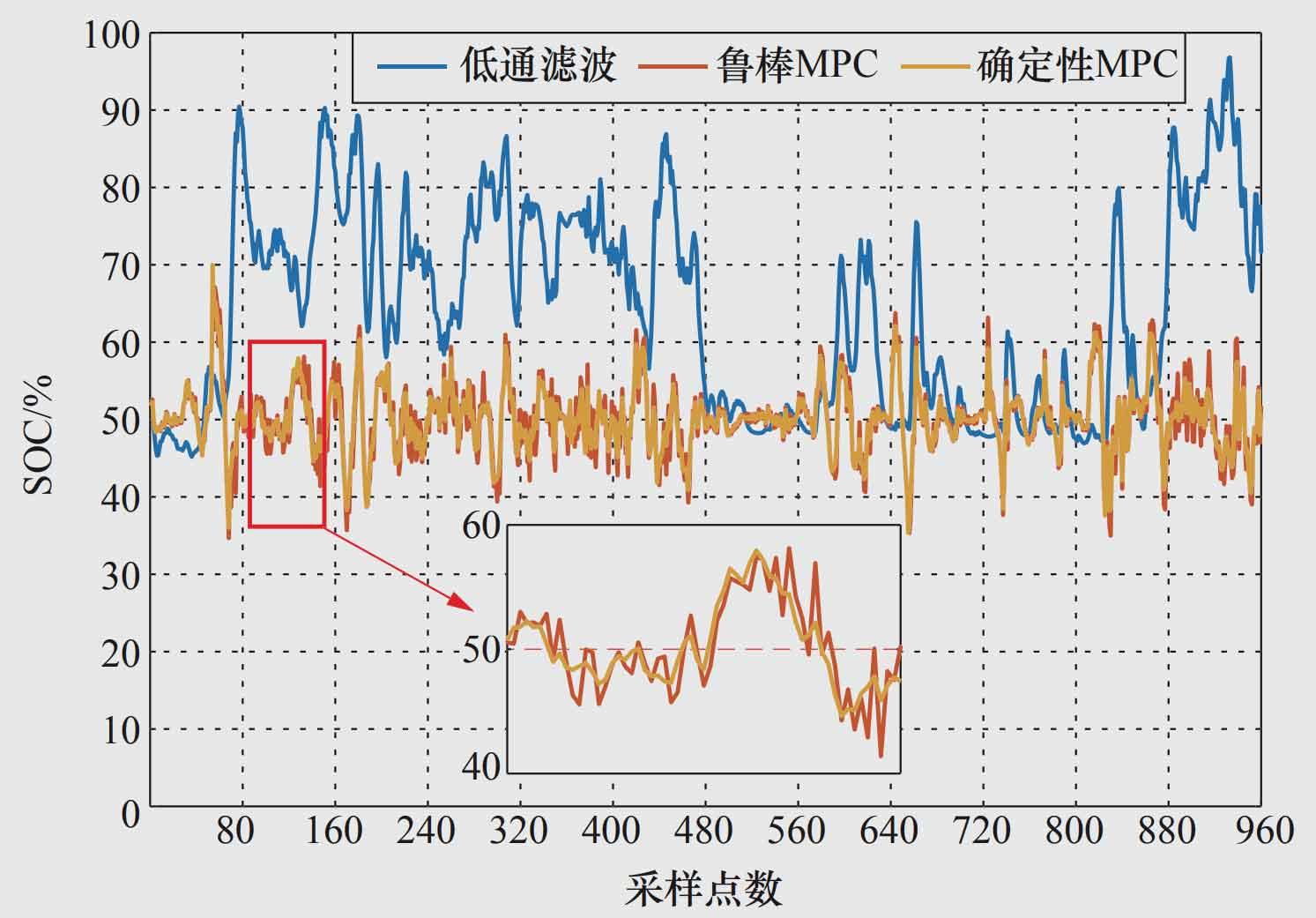
When suppressing wind power fluctuations, controlling the SOC of the energy storage plant around 50% of the center value can enhance its ability to cope with future extreme scenarios by increasing its output capacity. Figure 3 shows the changes in SOC curves of low-pass filtering method, deterministic MPC method, and robust MPC method. It can be seen that the low-pass filtering method did not optimize the SOC curve of the energy storage station, so its state of charge is always at a high level, increasing the safety risk of battery operation. Both the deterministic MPC method and the robust MPC method consider the optimization of the SOC curve of the energy storage plant, so the SOC curves of both methods are located near the 50% center value, ensuring that the energy storage plant always has sufficient margin.
4.3 Sensitivity analysis of wind power prediction error on suppression effect
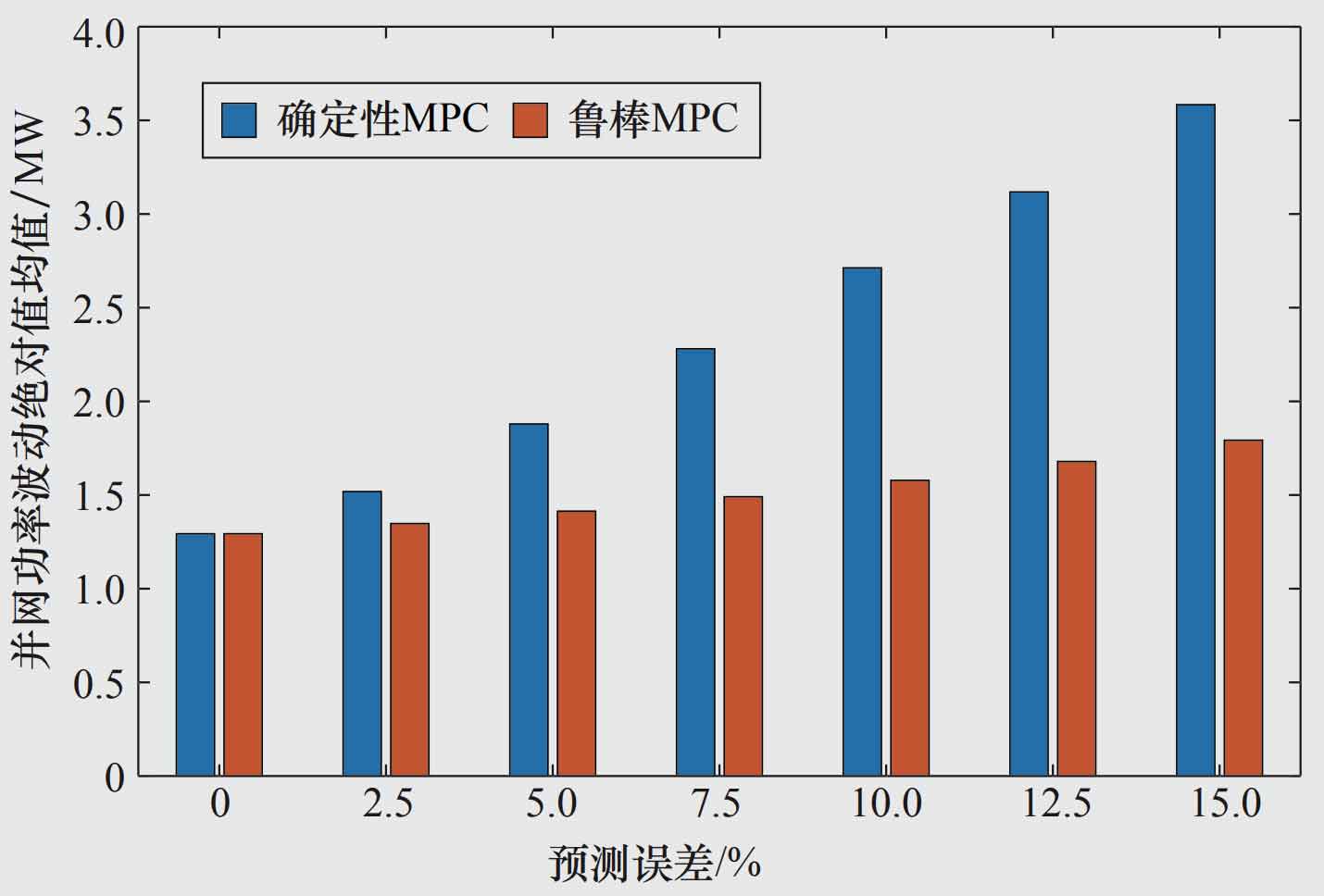
In order to analyze the impact of wind power prediction errors on deterministic MPC suppression methods and robust MPC suppression effects, Figure 4 shows the suppression effects of two methods under six different prediction error levels. It can be seen that when the wind power prediction error is 0, the robust MPC degenerates into a deterministic MPC. Due to the fact that the deterministic MPC method does not consider wind power prediction errors, as the prediction errors continue to increase, the smoothing effect of the deterministic MPC method becomes worse and worse. The robust MPC method considers the worst-case scenario where wind power prediction errors may occur. Therefore, as the prediction error increases, its smoothing effect does not show significant changes, proving the effectiveness of the proposed method in dealing with wind power prediction errors.
5. Conclusion
This article proposes a robust model predictive control technology for wind storage systems aimed at power suppression. In order to take into account the uncertainty of wind power, a output model of wind power was constructed using a box uncertainty set. We have established evaluation indicators for the effectiveness of wind power fluctuation mitigation, including the average fluctuation of grid connected power, the total energy of charging and discharging during the operation of energy storage stations, and the output coefficient of energy storage stations. To improve the solvability of the two-layer uncertain optimization model, the strong duality theory is used to transform the original two-layer model into a single-layer deterministic optimization model, and a set of linear inequality constraints are used to replace bilinear constraints through the large M method. Compared with deterministic MPC and low-pass filtering, the proposed Lubang MPC has better smoothing effect on wind power fluctuations and stronger adaptability to different levels of wind power prediction errors.
