Since the beginning of the new century, the significant increase in world energy consumption has once again made environmental and pollution issues a hot topic of global concern. In order to solve the secondary problems brought about by the energy crisis, the field of new energy has developed rapidly, and both wind energy, geothermal energy, solar energy, tidal energy, hydrogen energy, etc. have received widespread attention from researchers. The rise of these new energy sources has effectively solved the contradiction between economic development and environmental maintenance, while also driving the development and progress of downstream industries such as energy storage.
The proportion of new energy in the entire power supply is gradually increasing, and due to its own limitations, the imbalance between power supply and consumption is exacerbated, making the importance of energy storage systems increasingly high. How to flatten power supply peaks and valleys and improve the efficiency of energy storage systems is a key issue in ensuring economic benefits in the field of new energy. The traditional energy storage method mainly involves pumped energy storage, which converts excess electricity generated by new energy into potential energy for water. However, this method has significant limitations, low energy utilization efficiency, high construction costs, and is not conducive to vigorous development. The cost of chemical battery energy storage remains high, so new energy storage technologies are needed to complete the energy scheduling of the power system.
A new energy storage method is proposed, which combines gravity energy storage with battery energy storage to effectively solve the time difference problem of power dispatch. The whale algorithm is also proposed to model and simulate the power dispatch system. The experimental results show that the algorithm can effectively solve power system scheduling problems, with higher computational accuracy and stronger model convergence, and can be used to guide the design of the scheduling system.
1.New energy power dispatch system
1.1 Wind Resources
As a resource characteristic of new energy, wind energy has strong timeliness, uneven distribution of wind speed and other parameters, strong regional characteristics, and does not have good controllability like conventional energy. Therefore, for scheduling problems such as wind energy, it is necessary to use wind speed models for effective simulation, and describe them using normal distributions, Weibull distributions, etc. The probability model of wind speed in general can be described as:
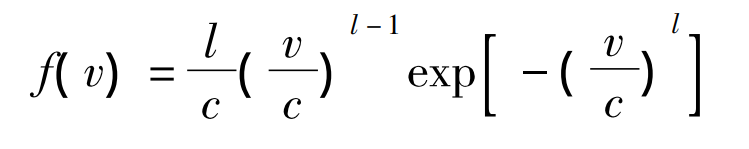
In the formula, v represents wind speed, l and c are shape factors and scale factors, respectively. The shape factor l can effectively reflect the distribution of wind speed. A smaller l indicates a wider range of wind speed distribution, while a larger l indicates a more concentrated wind speed distribution, highlighting the uncertainty of wind speed.
1.2 Solar energy
Solar energy relies on light and therefore has obvious temporal characteristics, with output during the day and the highest light intensity at noon. At night, there is almost no output of solar energy, which coincides with the staggered use of electricity by residents at night, making the use of solar energy dependent on the development of energy storage technology.
In order to effectively describe the resource distribution of solar energy and light intensity, experts and scholars have developed various models to describe it, mainly including functions such as gamma distribution and Boltzmann distribution. The gamma distribution, due to its wider applicability, can be used to describe the probability problem f (I) of solar energy intensity. It is represented as:
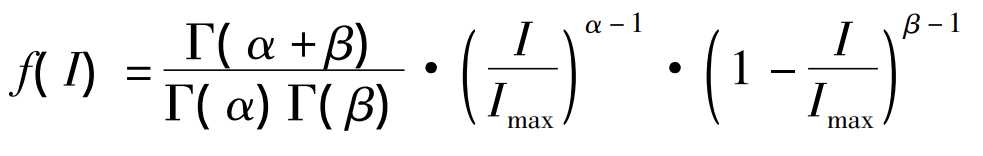
In the equation, Г Is a gamma function; Imax is the maximum intensity of light; α And β They are shape factors and scale factors, respectively. Similar to the distribution of wind speed, shape and scale factors determine the distribution of solar energy. Scale factors β The larger the size, the wider the distribution of solar energy, and vice versa, the more concentrated the distribution of solar energy.
1.3 Gravity energy storage model
The principle of gravity energy storage is simple and is a basic form of energy storage, characterized by low energy loss, high repetition rate, and safety and reliability. The main structure of a gravity energy storage system includes: energy storage platforms, heavy object transportation tracks, energy power stations, and corresponding distribution network systems.
When storing electrical energy, an electric motor is used to raise the weight to a certain altitude, thereby converting excess energy such as new energy into the gravitational potential energy of the weight. When it releases energy, the heavy object moves along the track towards a low altitude position, driving the generator to output electrical energy to the outside world. The speed at which the heavy object descends can effectively control the amount of output electrical energy, meeting the needs of the power dispatch system.
The system can store a huge range of energy and effectively regulate the system’s power output time, ranging from a few minutes to a few hours. The size of stored energy depends on the mass of the heavy object and the position of the heavy object at both ends. At the same time, multiple heavy object transport tracks are established to improve the operational efficiency of the system.
Based on the characteristics of the gravity energy storage system, it can be summarized that the model used in the energy storage process of the system is:
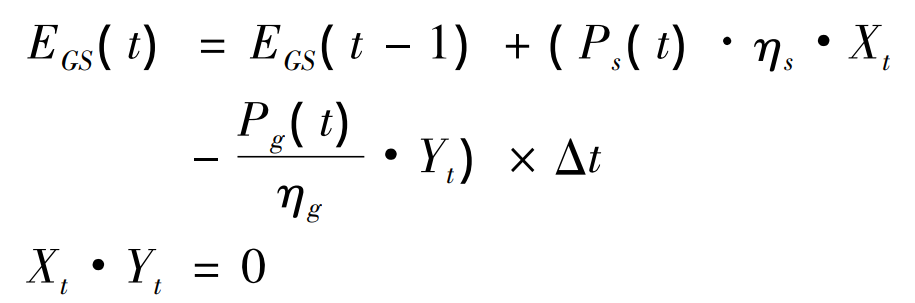
In the formula, EGS represents the storage capacity, Ps (t) and Pg (t) represent the charging and discharging power. η S and η G is the charging efficiency and discharge efficiency. For power system scheduling, especially the power distribution problem of new energy systems, optimization calculations are usually needed.
2.Improved Whale Algorithm
2.1 Whale algorithm
The Whale Algorithm is an efficient optimal solution solving algorithm derived from the hunting behavior mechanism of humpback whales, which uses bubbles as a net to trap prey and capture it.
This algorithm mainly includes three stages: prey containment, wall net restriction, and optimal value solving. By transforming the solution space, the position of the optimal solution can be continuously obtained and the final solution can be obtained.
The standard whale algorithm is prone to falling into local optima and has low efficiency in solving problems. By improving it and adding new flight strategies, it can significantly improve the spatial search ability of global solutions and obtain ideal solutions.
2.2 Improving the cosine convergence factor
In the process of solving the optimal solution, the convergence factor of the standard whale algorithm follows a linear transformation, which is not in line with the actual process of capturing prey, and the optimization effect is average. Processing the convergence factor, adding weight coefficients and cosine convergence, can effectively improve the efficiency of solving the optimal solution. For multi-objective optimization problems, due to the large amount of computational data, simple linear convergence factors can make the iterative process lengthy and cannot better achieve data optimization.
Using the cosine convergence factor, increase the convergence factor in the early stage to increase the spatial search range of the global solution, and reduce the convergence factor in the later stage to improve the accuracy of obtaining the optimal solution.
The expression for the cosine convergence factor is:
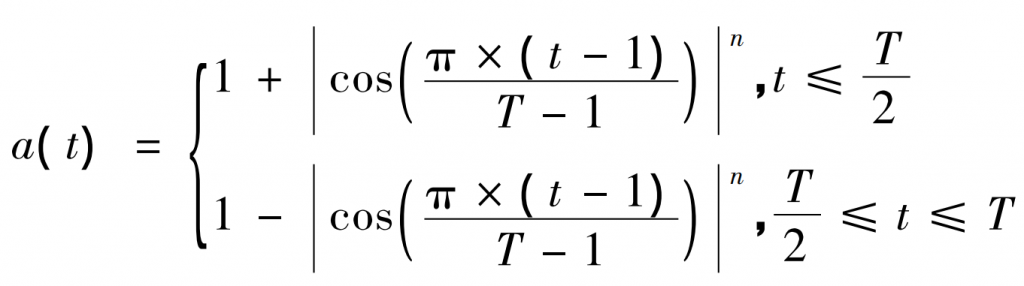
In the equation, a is the cosine convergence factor; T is the number of iterations; N is the adjustment coefficient. The experimental results show that when n is taken as 0 At 4 o’clock, the computational performance of this algorithm is better. Adding appropriate weight coefficients to the entire algorithm enhances the key search areas and improves the algorithm’s ability to solve optimal values.
2.3 Flight Strategy
Flight strategy is also a biological simulation method that simulates the foraging patterns of birds and fish, forming a food acquisition ability that conforms to their natural applicability, and is then used to obtain the optimal solution of the algorithm.
In this flight strategy, the organic combination of long and short steps forms an optimal solution search mechanism with food acquisition characteristics. Continuously changing the step size will make the search for extremum near the optimal solution more precise. Accompanied by partial long step search, this algorithm has a wider solution range and effectively overcomes the disadvantage of the original algorithm being prone to falling into local optima.
The probability distribution of flight strategies can be expressed as:
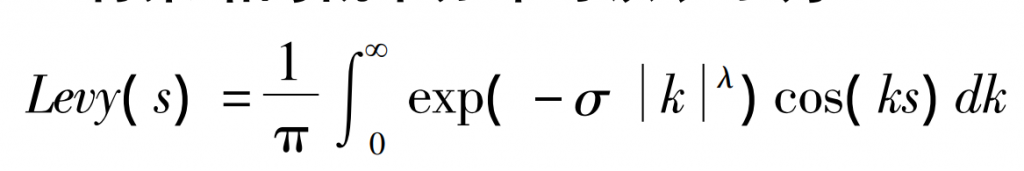
In the equation, λ And σ The distribution is the peak sharpness and span of the flight distribution.
2.4 Improved algorithm
On the basis of the original whale algorithm, make improvements. By adding a flight strategy to it, the search for the optimal solution is not limited to local optima. Therefore, applying it to energy scheduling can make the solution of the entire energy scheduling system more accurate.
3.Test results and data analysis
In order to verify the effectiveness of the algorithm proposed in this paper, the model and algorithm designed in this paper are simulated and validated using Matlab. The software version is selected as 2018b, the operating system is Windows 10, the device memory is 8GB, and the system CPU is configured as an i7-4790 processor.
3.1 System parameters
Taking into account the regional characteristics of new energy sources such as wind and solar energy, this study focuses on a certain area in northwest China, which is rich in this type of energy. The improved whale algorithm is used to optimize the power system allocation model. Finally, the optimal capacity configuration that meets actual needs is obtained, and based on this, a power generation plan is formulated to analyze the economic effectiveness of the gravity energy storage system.
The operating parameters of the distribution network are mainly set as follows: the comprehensive power shortage rate of the load is 0 2%, the range of self balancing rate is 0 35-1, with a scheduling response time of 20 minutes and a scheduling cycle of 24 hours. The capacity range of the energy storage mechanism is 0 2-1, storage methods include gravity storage and comparative battery storage. The comparison algorithm mainly adopts the improved whale algorithm, standard whale algorithm, and particle swarm optimization algorithm. The algorithm iteration number is set to 1000, and the population size is all set to 500. The power cost and other parameters used in the entire simulation system are shown in Table 1.
| Equipment | Installation costs | Maintenance costs | Replacement costs |
| 10kW wind turbine unit | ¥4860/kw | ¥200/KW/Year | ¥4260/kw |
| 0.2kW solar module | ¥4990/kw | ¥127/KW/Year | ¥4340/kw |
| 6kWh battery | ¥4050/kwh | ¥138/KWh/Year | ¥3720/kwh |
| Motor | ¥2560/kw | ¥80/KW/Year | ¥2560/kw |
| Gravity energy storage platform | ¥2410/kwh | ¥150/KWh/Year | ¥510/kwh |
| Energy storage track | ¥2000/Meter | ¥80/Meter/Year | ¥1600/Meter |
| Alternator | ¥2860/kw | ¥80/KW/Year | ¥2860/kw |
3.2 Gravity energy storage scheduling system
Due to the high altitude and large regional drop in the northwest region, it has abundant wind resources and new energy sources such as solar energy and geothermal energy.
Solar energy resources have strong temporal characteristics, with clear day and night, and different months receive different levels of solar radiation. The months with higher solar radiation intensity are mainly concentrated in April to August, while other months have lower radiation intensity, especially in the winter seasons of December and January. The distribution of wind speed in the region is almost opposite to that of solar radiation, with weaker winds from May to August, stronger winds in winter, and relatively weaker winds in January.
The wind energy in this region reaches its peak in spring, with wind speeds exceeding 9m/s. At this time, solar energy is weaker and energy output relies more on wind energy. At the same time, due to the increased demand for heating and other factors, the solar energy output is the highest in these two seasons due to high temperature, high light intensity, and low wind power. The situation in autumn and winter is similar, both belonging to the stage where wind power generation is relatively high and sunlight exposure is relatively high.
For the gravity energy storage power dispatch system, it is necessary to comprehensively consider the uncertainty of power generation in the region and fully utilize the imbalance between load and power supply to make corresponding power allocation. Prioritize the consumption of new energy sources such as wind and solar energy, and maximize the utilization of gravity energy storage. Establish a wind light gravity composite power supply system with cost optimization as the main objective.
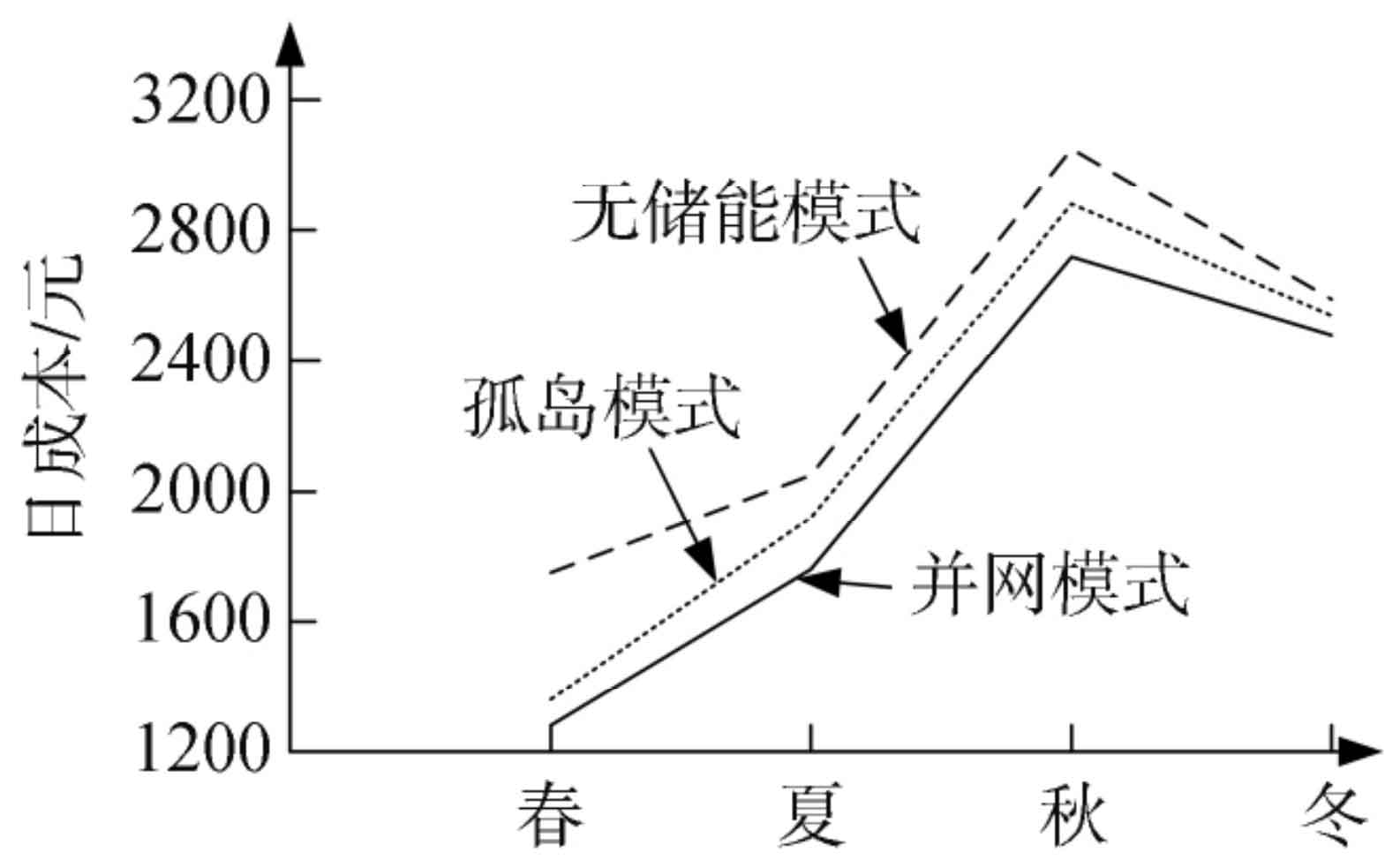
By utilizing a multi scenario analysis model and considering the operation of the gravity energy storage system power grid under different working modes, and distinguishing the four seasons, the system operation under different states is established. The operating costs of the system under different modes are shown in Table 2 and Figure 2.
| Mode | Grid connection | No energy storage | Isolated island |
| Abandonment probability | < 0. 1% | About 5% | < 1% |
| Average electricity purchase | 120kWh /Quarter | 2350kWh /Quarter | 0kWh /Quarter |
| Average electricity sales | 90kWh /Quarter | 0kWh /Quarter | 0kWh /Quarter |
| Average cost | ¥ 2070/Quarter | ¥ 2300/Quarter | ¥ 2150/Quarter |
The gravity energy storage power system mainly includes three schemes: grid connected transmission, power islanding, and no energy storage.
From the experimental results, it can be seen that for the mode without energy storage, the probability of abandoning new energy is the highest. Due to the absence of energy storage facilities, the energy utilization rate is low during peak electricity consumption, which happens to be when the energy cannot be supplied. The average daily cost is close to 2300 yuan, and the electricity purchase is also the highest among the three modes. For the island mode, the utilization rate of new energy is significantly higher than that of the mode without energy storage system. Due to the fact that the electricity generated by new energy can be stored and effectively applied, the probability of abandoning new energy has significantly decreased. The average cost of the system in this mode is around 2150 yuan, but due to the insufficient energy storage capacity to fully meet the power demand, it is necessary to increase the energy storage system, which will further increase the operating cost.
The grid connected mode has the highest operating efficiency among all modes, with a abandonment rate of less than 0.1% in spring. The system has strong self balancing ability in other seasons, and the demand for power supply from the grid is not too high. The average purchased electricity is about 120kWh. The operating cost is about 2070 yuan, and compared to the other two modes, the cost in this mode has decreased by about 9% and 4% respectively. There is also no power shortage in the system, proving that this mode is the most economical and reliable.
3.3 Comparison of Gravity Energy Storage and Battery Energy Storage
For the comparison of energy storage systems in new energy networks, gravity energy storage and battery energy storage are used, with the same capacity selection. A horizontal comparison can be made, and the comparison results are shown in Figure 3.
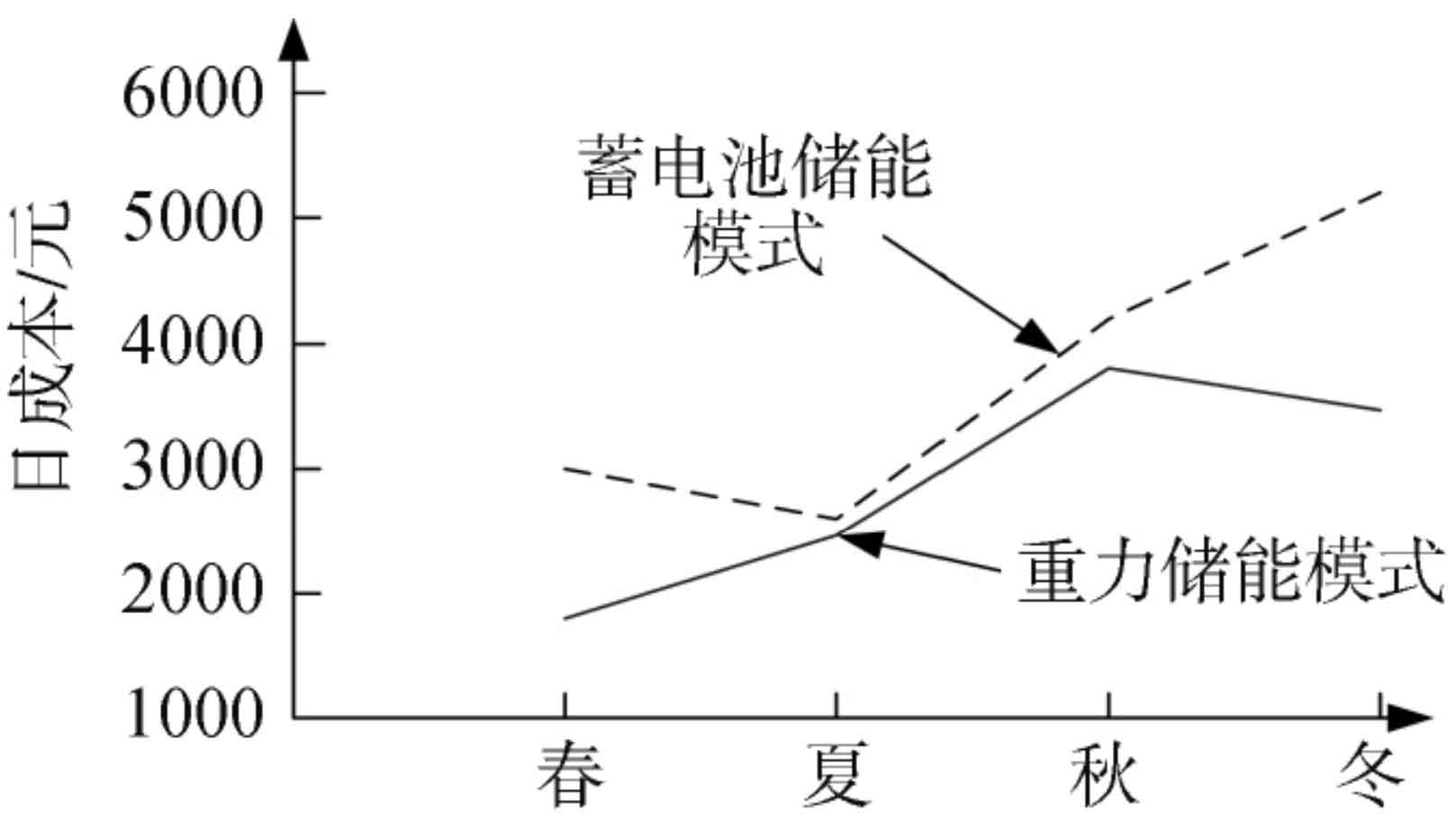
As shown in Figure 3, the cost of gravity energy storage is lower than that of battery energy storage in all seasons. The characteristics exhibited by different seasons are slightly different, with gravity energy storage having the lowest cost in spring and battery energy storage being better in summer.
In spring, wind energy generates a large amount of electricity, while solar energy is weak. Gravity energy storage systems respond faster to large amounts of energy and store electricity more promptly. When using batteries for energy storage, due to delayed energy storage, users need to purchase additional electricity when consuming energy, which increases the cost of electricity consumption.
In summer, wind energy weakens and solar energy generates a large amount of electricity, which can effectively cope with daytime electricity consumption. The demand for energy storage is not strong, and the difference between the two energy storage methods is not significant. However, the cost of gravity energy storage is still lower than the cost of batteries.
The load situation in autumn is similar to that in spring, but due to seasonal reasons, the electricity generated by new energy is ultimately limited and cannot fully meet the electricity demand of users. Both energy storage methods require users to purchase electricity, resulting in increased costs.
In winter, it belongs to a high load state of electricity consumption, where the saved wind power generation is large and the solar power generation is small. Due to the high load requirements of electricity, both energy storage methods require high capacity. Gravity energy storage is more suitable for large-capacity energy storage systems, and batteries are suitable for situations where the charging and discharging frequency is high but the capacity is not too large. The cost of gravity energy storage is lower than that of battery energy storage.
The comparison of annual test results shows that the area has high altitude and high air volume, so the power supply continuity of wind power generation is stronger, while the output of solar energy can only be better supplied during the day, and is greatly affected by radiation intensity, making a significant contribution only in summer. Therefore, in order to optimize the distribution costs in the region, it is necessary to increase the installed capacity of wind power and reduce the proportion of photovoltaic power generation capacity. After calculation, the optimized installed capacity of the region is 1900 kW for wind power and 420 kW for solar energy, with a ratio of approximately 4 At 5:1, the daily cost of gravity energy storage power grids is lower than that of batteries, and the overall cost is reduced by about 20%.
3.4 Node Model Validation
Add the capacity optimization configuration results from the previous section to the standard IEEE-3 node model. By adding a corresponding wind power capacity of 1900kW at node 32, a corresponding photovoltaic capacity of 400kW at node 24, and adding gravity energy storage and typical loads to the system. The modified IEEE-33 node model is shown in Figure 4.
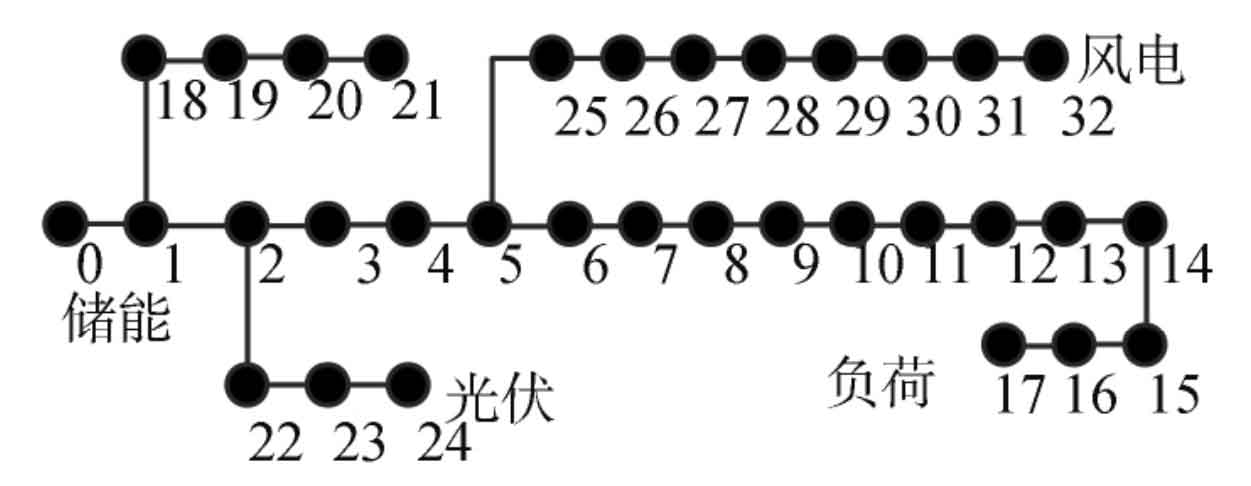
For this node model, three different states were set for comparison, considering the initial state, added load state, and comparison of the situation after the new energy gravity energy storage mechanism was put into operation. The comparison results are shown in Figure 5.
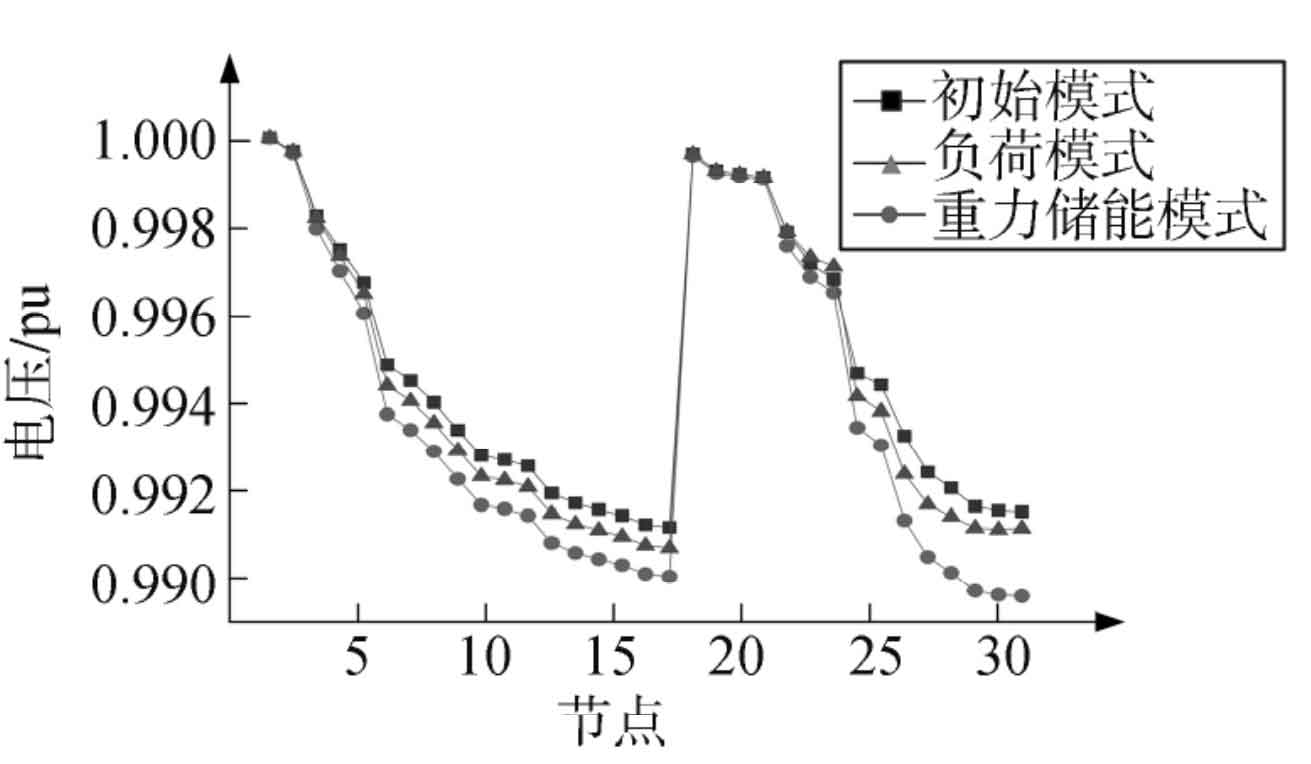
In Figure 5, it can be seen that the initial voltage of each node decreases with the increase of distance, which conforms to the basic law. Due to the maximum distance between node 17 and the power supply section, the voltage at this point is the lowest, with a per unit value of approximately 0 9913.
After adding the system load and the new energy gravity energy storage system separately, the node voltage has undergone certain changes. After simply adding the load, the voltage value of node 17 further decreases, and the standard unit value drops to 0 9895.
When a new energy gravity energy storage system is added to the system, the lowest point voltage per unit value increases to 0 Compared with pure grid power supply, the voltage drop of the new system has significantly decreased from about 17% to 4 5%, the overall voltage of the system is also closer to the original voltage, indicating that the system has important application value and significance for maintaining the stability of the power grid.
3.5 Algorithm Comparison
In order to verify the superiority of the algorithm proposed in this paper, the improved whale algorithm, standard whale algorithm, and particle swarm optimization algorithm designed in this paper were compared. The convergence of the algorithm for typical days is shown in Figure 6.
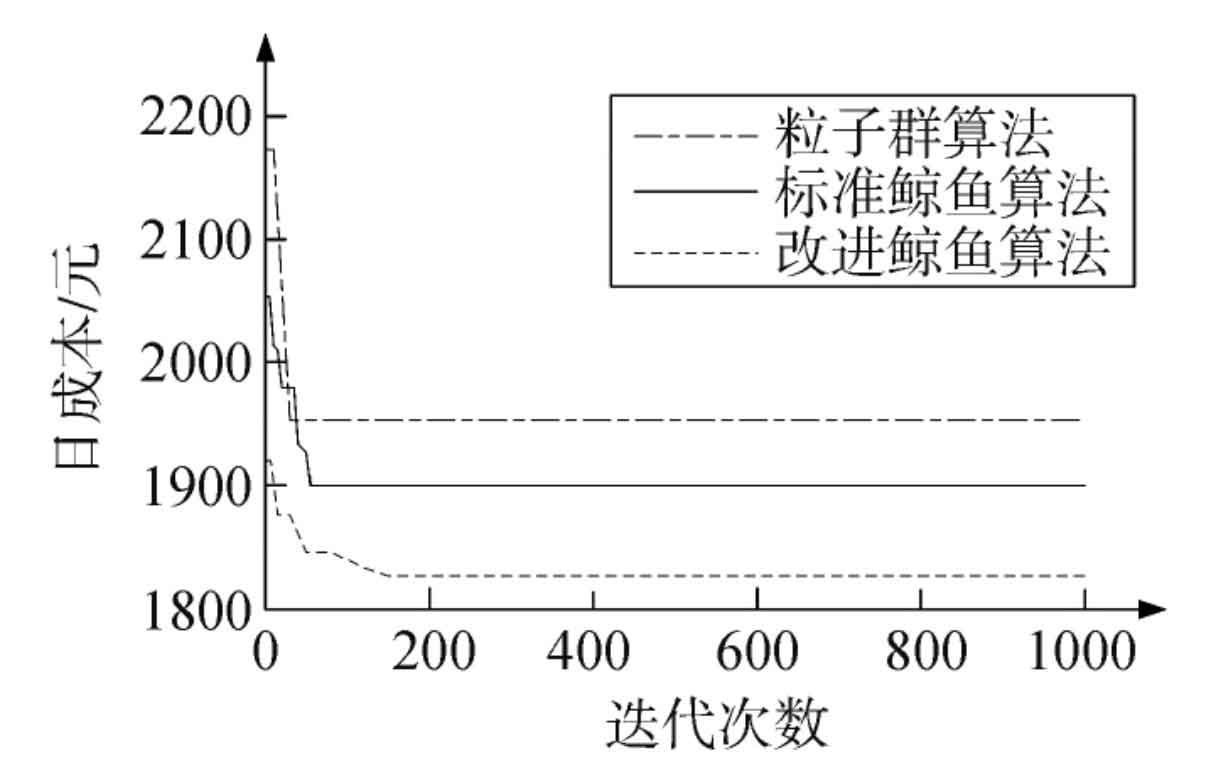
As shown in Figure 6, both the standard whale algorithm and the improved algorithm entered the convergence stage early in the initial stage. The particle swarm optimization algorithm and the standard whale algorithm entered the stop search stage early, indicating that the above two algorithms have entered a local optimal state. After entering the local optimum, the improved whale algorithm jumped out in the 70th and 116th iteration processes, and ultimately obtained the optimal value in the 243th generation. The calculation results of the optimal cost show that the improved whale algorithm is 5% and 8% lower than the standard whale algorithm and particle swarm optimization algorithm, respectively. Prove that the algorithm proposed in this paper has better convergence and search accuracy.
4.Conclusion
In response to issues such as low utilization of new energy, especially the scheduling model of new energy storage systems, this paper proposes a new energy gravity energy storage system based on gravity energy storage. The system uses an improved whale algorithm as a solution for power resource scheduling. On the basis of fully utilizing the strong solving ability of the Whale Algorithm, this algorithm greatly expands the solving range of the algorithm by improving the convergence factor and introducing flight mechanism, improves the computational ability of the algorithm, and greatly improves the convergence and accuracy of the model. By comparing with other algorithms, the optimal cost of this algorithm is lower than the calculation results of other algorithms. Through comparison with other modes, it is found that the grid connected mode using gravity energy storage has better economic efficiency and lower electricity costs, making it suitable for distribution systems with more new energy applications.
