Under the strategic background of sustainable energy development, the proportion of new energy represented by photovoltaic and wind power is gradually increasing. However, a high proportion of new energy can lead to power fluctuations and reduced inertia in the power system, posing new challenges to the safe and stable operation of the new power system. To this end, multiple provinces and regions in China have issued new energy distribution and storage policies, setting the minimum proportion of supporting energy storage capacity for new energy stations to solve the problems caused by new energy. Among them, battery energy storage has been widely used due to its relatively mature technological advantages. Commonly used batteries include lithium batteries, lead-acid batteries, hydrogen fuel cells, etc., which are collectively referred to as energy storage batteries in this article. According to statistics, 25.4 GW of new energy storage projects have been put into operation globally in 2021. In the “Implementation Plan for the Development of New Energy Storage during the 14th Five Year Plan” issued by the National Development and Reform Commission and the National Energy Administration, battery energy storage is listed as an important part of new energy storage construction, and it is explicitly proposed to enter the stage of large-scale development by 2025. At present, research on the large-scale grid connection of battery energy storage is mainly divided into two categories: one focuses on the steady-state characteristics of battery energy storage, involving configuration planning, optimal power flow, energy management, etc. By considering steady-state factors such as location, capacity, power, etc., to achieve economic, environmental, and reliability goals; Another type focuses on the dynamic characteristics of battery energy storage, focusing on the impact of battery energy storage grid connection on the stability of AC and DC systems. Among them, the analysis object can be divided into two categories based on whether it has been linearized: small disturbance stability and transient stability. The research on small disturbance stability based on linearized models of battery energy storage grid connected systems is the most extensive, while transient stability is limited by the complexity of mathematical models, and there have been no systematic reports on large-scale battery energy storage. Therefore, this article takes the small interference stability of battery energy storage grid connected systems as the starting point, and summarizes the impact of battery energy storage dynamic characteristics on the stability of AC and DC grid connected systems, which has practical significance for guiding the development of energy storage.
The structural characteristics of battery energy storage are similar to those of new energy sources such as photovoltaics and wind turbines, both of which are connected to the grid through power electronic converters. Currently, some studies have simply equated battery energy storage structures with new energy equipment, but there are certain differences between the two, specifically manifested in the following three aspects.
① Differences in power supply characteristics: Energy storage batteries are composed of numerous individual batteries in series or parallel. Without considering battery losses, batteries as the power source for battery energy storage exhibit voltage source characteristics, i.e. constant DC voltage; The mainstream new energy generally adopts maximum power point tracking control, and the power generation side presents the dynamic characteristics of the power source, that is, the output power is constant.
② Differences in power characteristics: Battery energy storage can actively supply power to the grid connected system as a power source, and can also actively absorb excess energy from the grid connected system as a load, with bidirectional power; New energy is a typical power generation equipment, and its output power depends on the external environment and cannot actively change the power flow direction.
③ Control characteristics: Battery energy storage has a large amount of adjustable energy reserves, using traditional grid following control for damping improvement, power regulation, etc. It can also use grid forming control for active frequency and voltage support, etc; However, mainstream new energy sources do not have adjustable energy reserves under maximum tracking point power control and cannot provide active support. Although research has proposed grid control for new energy sources, energy storage devices (such as DC voltage sources, supercapacitors, etc.) are added.
Therefore, simply equating the stability of battery energy storage grid connected systems to the stability of new energy grid connected systems has limitations and cannot meet the research needs of safe and stable operation of battery energy storage scale grid connected systems. Due to the diversity of battery energy storage characteristics, the types and range of factors that affect the stability of small disturbances in grid connected systems are even greater than those of new energy sources. For example, it is concluded that changes in parameters such as voltage, internal resistance, and capacity ratio of energy storage batteries will worsen the stability of grid connected systems; The conclusion is drawn that under a specific power flow direction, battery energy storage may exhibit negative resistance characteristics, leading to instability of the grid connected system. These influencing factors are not involved in the stability research of traditional new energy grid connected systems. In addition, an improved active damping control method based on energy storage is proposed to address the sub/super synchronous oscillation problem caused by the connection of the direct drive wind power grid connected system to the weak current grid; An additional damping control method based on active and reactive power control loops is proposed for multimodal oscillations in the system. These studies have confirmed that the control objective of battery energy storage is not limited to its own power and voltage, but also has the ability to improve the stability of grid connected systems. The primary control objective of new energy is to maximize transmission power, which can lead to more oscillation events. There are few research reports on the positive impact of new energy on system stability.
In order to systematically analyze the influencing factors and instability risks of the stability of battery energy storage grid connected systems, clarify the challenges that the future large-scale grid connection of battery energy storage will bring to the small interference stability of AC and DC systems, summarize the control methods of battery energy storage connected to AC and DC systems, and analyze the instability mechanism of small interference stability of a single battery energy storage grid connected system, Explored the application bottlenecks of existing research results in the large-scale grid connected system of battery energy storage, pointed out future key research directions, in order to provide reference for the large-scale development and construction of battery energy storage.
1.Structure and control of battery energy storage
1.1 Battery energy storage and grid connection system
In order to meet the requirements of grid connected systems for battery energy storage voltage, power, and capacity, energy storage batteries are composed of a large number of individual batteries in series and parallel. The structure of the energy storage battery is shown in Figure A1 of Appendix A. The voltage of a single battery is VB, the rated current is BI, the rated power is PB, and the rated capacity is CB. When N batteries are connected in series, the voltage of the energy storage battery is NVB, the current is BI, the rated power is NPB, and the rated capacity is CB; When N batteries are connected in parallel, the voltage of the energy storage battery is VB, the current is N BI, the rated power is NPB, and the rated capacity is NCB. In order to meet the voltage and power requirements of battery energy storage at the same time, the above two connection methods are usually used simultaneously. For example, when there are M battery modules in parallel and each battery module has N batteries in series, the voltage of the energy storage battery is NVB, the current is MBI, the rated power is MNPB, and the rated capacity is MCB.
From the above analysis, it can be seen that the dynamic characteristics of energy storage batteries are closely related to individual batteries. At present, the general method for establishing battery models is to conduct a detailed study of the electrochemical characteristics of batteries to construct the impedance relationship between their input current and output voltage, which is equivalent to an impedance expression influenced by various parameters such as materials and environment. Common single cell models include the Rint model, Thevenin model, second-order RC model The partnership for a new generation of vehicles (PNGV) model, etc. Obviously, for different batteries in different environments, their external characteristics are time-varying, and battery model construction is actually a complex problem involving multiple disciplines such as materials and circuits. But when focusing on stability issues, the battery model can be equivalent to a model where a constant voltage source V0 and a constant internal resistance R0 are connected in series, as shown in Figure A1 of Appendix A. The reason is that the time scale involved in dynamic stability issues is generally within the second level (including subsynchronization, supersynchronization, harmonics, etc.), and within this time scale, the electrochemical characteristics of the battery will not undergo significant changes. Therefore, it is relatively accurate and convenient to use a simplified model of a battery with voltage source series internal resistance for stability research. Here, the battery modeling method is cited for explanation.
For a single generalized battery, its external characteristics can be expressed as:
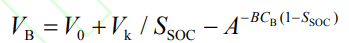
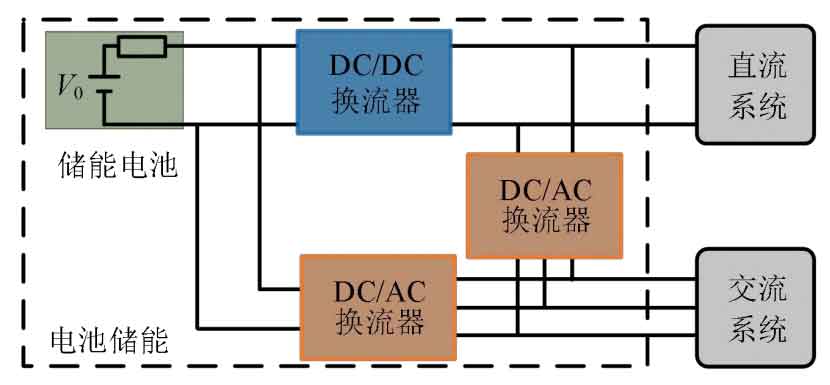
In the formula: Vk is the polarization voltage; A. B is the parameter that determines the charging and discharging characteristics of the battery; SOC S is the state of charge of the battery. Parameters A, B, and Vk can be adjusted to simulate the charging and discharging characteristics of specific battery types. At the second level time scale, the above parameters can be regarded as constants, so the battery can be constructed as a simplified model with a voltage of V0 and an internal voltage drop of V0-VB. It is worth noting that the model simplification error will gradually accumulate with the increase of battery capacity and quantity, which may lead to deviation in stability results. However, considering that the current capacity of a single battery is still limited, no research has pointed out that this simplification can lead to deviation in stability results. Therefore, the modeling method of equating the battery model to a constant voltage source and constant internal resistance series model has been widely adopted. The battery energy storage grid connection system is shown in Figure 1. There are two grid connection methods for battery energy storage: one is to integrate it into the DC system through a DC/DC converter; Another method is to integrate into the AC system through DC/DC, DC/AC converters, or directly integrate into the AC system through DC/AC converters. Different inverters have various topological structures corresponding to different energy conversion efficiency and quality. However, the average value model of inverters is often used in studying small interference stability. Therefore, this article will not elaborate on the topology of inverters.
1.2 Control of battery energy storage in DC systems
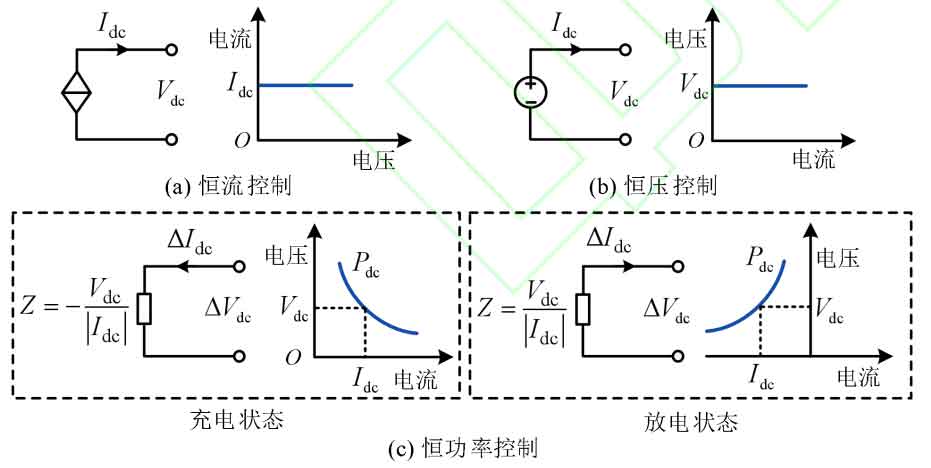
When battery energy storage is integrated into the DC system, the common DC/DC converter control is shown in Figure 2. In the figure, Vdc and DC I respectively represent the DC voltage and current output of the battery energy storage; Pdc is the active power output of battery energy storage; The superscript ref represents the reference value of the variable in the DC/DC converter control system. When BI or Pdc is positive, the battery energy storage operates in a discharge state; When BI or Pdc is negative, it operates in a charged state.
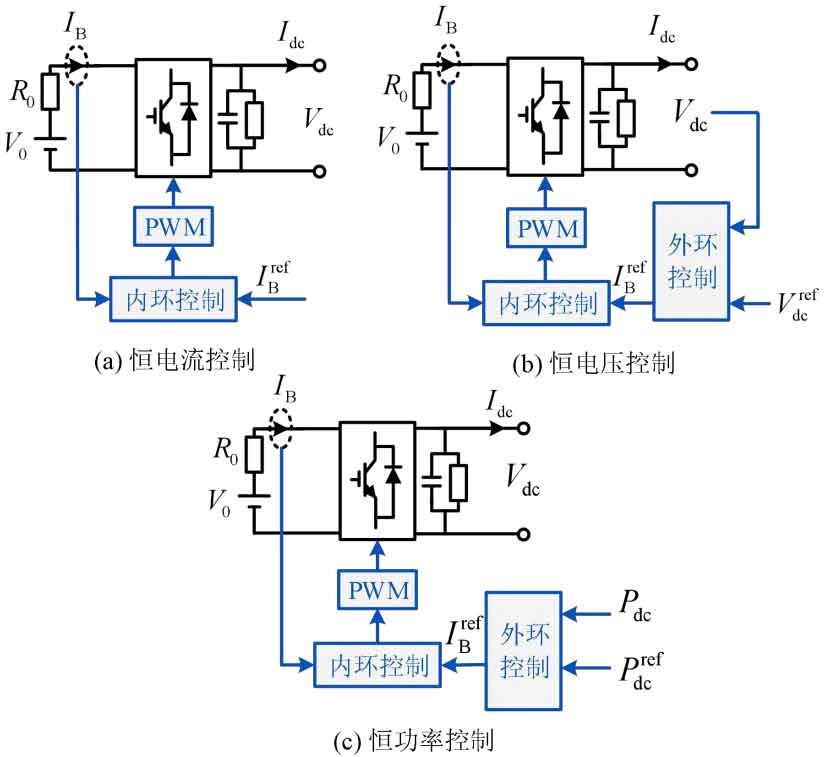
As shown in Figure 2 (a), constant current control generates an inner loop control signal by calculating the deviation between the DC current reference value and the actual value, which is used to maintain a constant DC current output of the DC/DC converter. Constant current control has the characteristics of high control accuracy and fast dynamic response, but it can generate periodic current errors and is suitable for situations with high dynamic indicators. Based on constant current control, constant voltage control and constant power control can be achieved by adding an outer loop control, as shown in Figure 2 (b) and (c), respectively. Constant voltage control (constant power control) generates an outer loop control signal by calculating the deviation between the DC voltage reference value and the actual value (the deviation between the power reference value and the actual value), and then generates the DC current reference value through the outer loop control. Then, the tracking of the current reference value is achieved through the inner loop control. Constant voltage control can maintain a constant DC bus voltage, but compared to constant current control, it adds voltage outer loop control, which increases the uncertainty of the impact on the stability of the DC system. Constant power control changes the constant voltage characteristics of battery energy storage, resulting in battery energy storage exhibiting constant power characteristics similar to new energy, resulting in stability issues different from constant voltage control.
1.3 Control of battery energy storage in AC systems
When battery energy storage is integrated into the AC system, common DC/AC converter controls are shown in Figure 3, including two types: grid following control and grid building control. In the figure: s Ι Is three-phase AC current; Vs is the three-phase AC voltage; S θ The phase angle of the inverter output voltage; V is the amplitude of the grid connected voltage of the inverter.
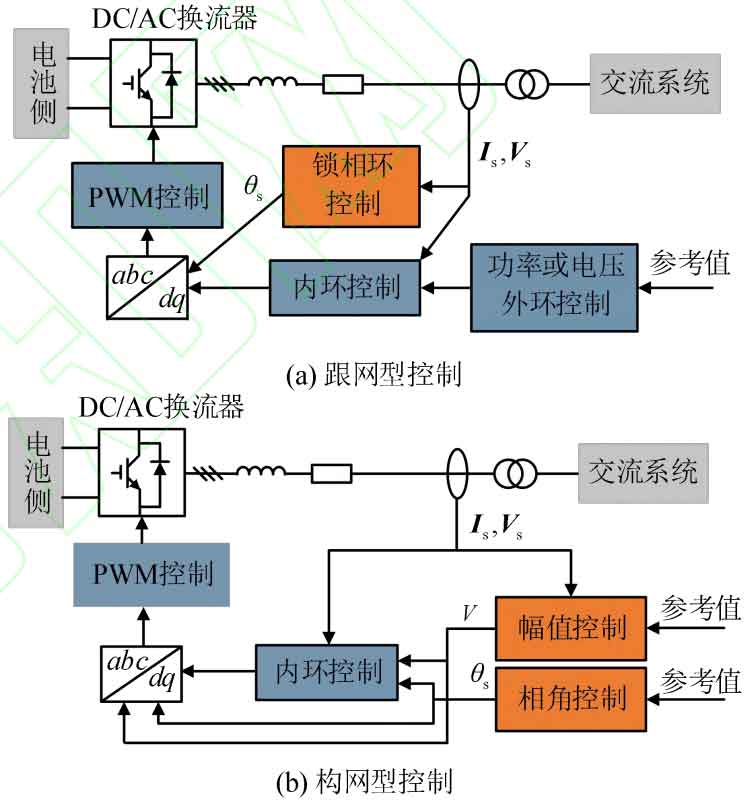
Figure 3 (a) shows the grid following control block diagram of the battery energy storage DC/AC converter, including four links: outer loop control, inner loop control, phase-locked loop control, and pulse width modulation (PWM) control. Among them, PWM control is used to generate control signals for converter switching elements; Phase locked loop control is used to achieve synchronization between the inverter and the AC system; Inner loop control is used to achieve tracking and decoupling of d-axis and q-axis control variables; The outer loop control is used to specify the control objectives of the inverter, such as AC/DC voltage, active power, and reactive power. The network control shown in Figure 3 (b) mainly includes four links: phase angle control, amplitude control, inner loop control, and PWM control. Among them, phase angle control can be dynamically adjusted based on frequency and power control commands θ S; Amplitude control is mainly used to maintain V constant. Some literature also involves the inner loop control link, which is used to achieve current limiting, but does not affect the basic control architecture of voltage phase angle and amplitude. The grid type control adopts a power synchronization principle similar to synchronous generators, does not rely on phase-locked loops, and has active support capabilities such as frequency and voltage.
The differences between battery energy storage and new energy control are shown in Table 1. Although the control types of new energy and battery energy storage are basically the same, the specific control objectives are different. New energy is similar to a power source under maximum power point tracking control, so the control objective of its DC/AC converter must involve DC voltage, such as the droop control of fixed DC voltage or DC voltage participation, so that the DC/AC converter can be similar to a power balance node, achieving a balance between injected power and output power on the DC side. Energy storage batteries, similar to constant voltage sources, can achieve power balance on their own. Without considering DC/DC converters, the control objective of battery energy storage DC/AC converters must involve active power or frequency, such as droop control with fixed active power or active power participation, to achieve specified power output; If DC/DC converters are considered, the selection of control objectives for DC/AC converters will vary depending on the control characteristics of the DC/DC converters.
| Equipment | Source side control | Network side control | Control Objectives |
| Battery energy storage | None | Heel net type | Power, frequency, or droop control |
| Battery energy storage | Constant voltage | Network type | Power, frequency, or droop control |
| Battery energy storage | Constant current | Heel net type | DC voltage or droop control |
| Battery energy storage | Constant power | Network type | DC voltage or droop control |
| New energy | Maximum power point tracking (widely used) | Heel net type | DC voltage or droop control |
| New energy | Non maximum power point tracking (not widely used) | Follow net type/build net type | Frequency, voltage, or droop control |
For new energy sources without additional energy storage devices, their DC side capacitors are difficult to support the energy required for grid type control. Therefore, new energy DC/AC converters under maximum power point tracking control are not suitable for grid type control. At present, although some studies have proposed the control of new energy participation in power support, such as providing certain power support by operating new energy at non maximum power points, releasing the rotational kinetic energy of new energy generators, etc., the direction of power support is unidirectional, and excess power cannot be absorbed from the grid, which does not meet the applicable conditions for bidirectional power control in grid construction. In addition, this type of control will reduce the power generation efficiency of new energy, which is not in line with China’s policy of strongly supporting full grid connected power generation of new energy. Therefore, it has not been widely applied. Therefore, this article will not delve into this type of object. And the battery has a constant voltage characteristic, so the DC/AC converter for battery energy storage can not only use grid type control, but also choose different control objectives based on the different control objectives of the DC/DC converter, with diverse control strategies.
Based on the constant voltage characteristics of batteries, many literature have proposed diversified control strategies to enable battery energy storage to have multiple additional functions, as shown in Figure A2 in Appendix A. Figure A2 (a) takes the frequency deviation of the AC system as the input signal, and through control links such as proportion, phase shift, and compensation, adds a new input signal to the external loop control to improve power oscillation damping; Figure A2 (b) takes the current on the inverter line side as the input signal, passes through a filter and a proportional link, and adds a new voltage deviation signal to the reference control variable output by the inverter control link to suppress subsynchronous oscillations in the wind farm; Figure A2 (c) takes the system frequency and voltage amplitude deviation as input signals, and adds new input signals to the inner loop control through PI control to eliminate the risk of grid connected new energy torsional vibration; Figure A2 (d) focuses on the phase angle control of the virtual synchronous generator, using angular velocity deviation as input and adding a new damping torque signal to improve low-frequency oscillation damping.
2.The impact of battery energy storage on the stability of DC systems
2.1 Stability of a single battery energy storage grid connected system
2.1.1 Consider battery energy storage control
Figure 4 shows the analysis process of battery energy storage grid connected system mode. In the picture: Δ Represents the amount of change in a variable; AB, Adc, and AS respectively represent the state spaces of energy storage batteries, battery energy storage, and battery energy storage grid connected systems; λ B λ DC λ S represents the characteristic values of energy storage batteries, battery energy storage, and battery energy storage grid connected systems; ZB (s), Zdc (s), and ZS (s) respectively refer to energy storage batteries, battery energy storage, and battery energy storage grid connection
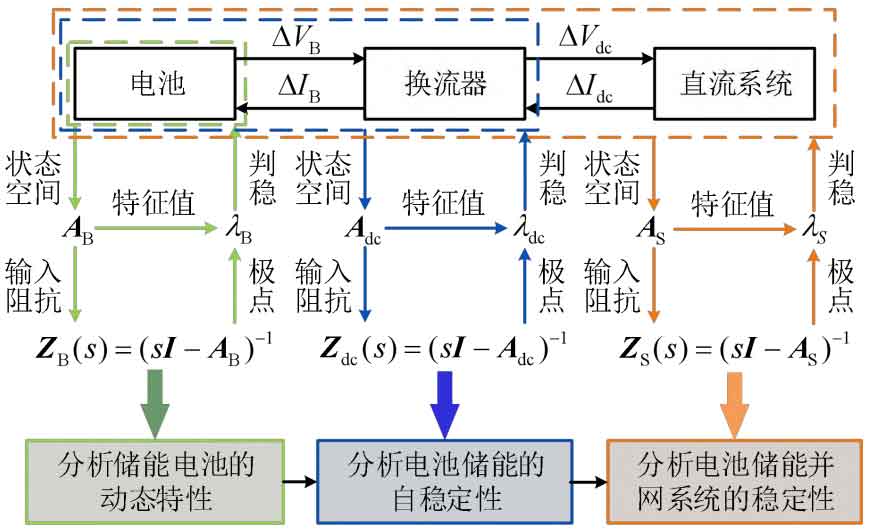
The input impedance matrix of the system, where s is the Laplace operator; I is the identity matrix. From Figures 2 and 4, it can be seen that improper adjustment of the control parameters of the battery energy storage DC/DC converter can lead to its own instability. If connected to the grid under these conditions, it will also cause the DC system to become unstable. Reference [38] is based on the characteristic equation of the energy storage control system, and determines the range of control parameters through the Root stability criterion, ensuring the stability of the battery energy storage control system before grid connection. On the premise of self stability of battery energy storage, the main reason for the instability of a single battery energy storage grid connected system is the dynamic interaction between battery energy storage and the DC system. From the perspective of battery energy storage, the influencing factors of dynamic interaction between the two mainly include energy storage battery parameters, power flow direction, and control parameters. Considering the charging and discharging characteristics of energy storage batteries, the battery was involved in the control process, and the influence of battery parameters and their control process parameters on the root trajectory of the DC system was analyzed. Reference [40] considers the dynamic process of energy storage batteries and inverters, establishes a state space model, and uses pattern analysis to obtain the conclusion that the battery will increase internal resistance due to overcharging and discharging, and the decrease in battery voltage will worsen the stability of the DC system. The above studies have all considered the dynamic characteristics of batteries, but in order to reduce the complexity of modeling, many studies have ignored the dynamic characteristics of batteries and simplified them to constant voltage source series internal resistance. For example, reference [41] analyzed the impact of load on the stability of energy storage inverters based on pattern analysis method, and verified that the interaction between battery energy storage and other devices can affect the stability of DC systems; Based on the time-domain simulation method, the influence of the length of the battery energy storage DC side cable on DC stability was analyzed, and it was concluded that increasing the battery energy storage DC line will reduce the stability of the DC system.
The above research has confirmed through time-domain simulation and mode analysis that dynamic links such as energy storage battery parameters and DC/DC control all have risk factors that can worsen the stability of the DC system. When considering more dynamic links, the model of battery energy storage will become more complex, making it difficult to clarify the correlation between different influencing factors. Although time-domain analysis and mode analysis methods still have universality in such scenarios, time-domain simulation methods are difficult to provide quantitative analysis results, and mode analysis methods have the problem of large computational load and even dimensionality disaster when facing high-order systems, which cannot accurately reveal the mechanism of the impact of single battery energy storage on the stability of DC systems. In order to reveal the mechanism of the impact of battery energy storage access on the stability of DC systems, scholars have attempted to use frequency domain analysis. For example, based on the Nyuist curve, the differences in the impact of battery energy storage on the stability of DC systems under three control strategies of constant current, constant voltage, and constant power were compared, and the conclusion was drawn that constant power control exacerbates the risk of DC voltage oscillation compared to other controls; Based on the impedance method, the influence of battery energy storage capacitors on the stability of the DC system was analyzed, and it was concluded that excessive capacitance can reduce the impedance ratio at the resonance stable point, leading to system instability; Summarized the general process and commonly used impedance criteria for impedance analysis of DC systems, as shown in Figure A3 of Appendix A.
2.1.2 Simplify battery energy storage control
Although the concepts such as impedance in frequency domain analysis have more physical significance, due to the complexity of the transfer function, it is still necessary to draw its Nyquist curve or impedance curve during analysis, making it difficult to obtain an analytical solution that leads to negative impedance. Moreover, there is a lack of direct theoretical proof, which promotes further simplification of battery energy storage models.
The simplified model of battery energy storage and its external dynamic characteristics are shown in Figure 5. The constant current controlled battery energy storage can be simplified as a constant current source/charge, with an external resistance of 0; The battery energy storage controlled by constant voltage can be regarded as a constant voltage source, with an infinite external resistance. In theory, constant current/load and constant voltage sources do not affect the oscillation mode of the system. The battery energy storage with constant power control can be simplified as a constant power source/load.
The change in active power output when combined with battery energy storage is 0, i.e Δ Under the condition of Pdc=0, the input impedance Z0 of battery energy storage in the simplified model can be obtained as:
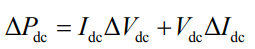
From equation (3), it can be seen that when the energy storage absorbs power (DC I is positive and consistent with the positive direction), the battery energy storage presents a negative impedance; When the energy storage emits power (DC I is negative and opposite to the positive direction), the battery energy storage exhibits a positive impedance. Therefore, the mechanism of the instability of the DC system caused by battery energy storage is very clear, that is, the negative resistance characteristic presented in the constant power charging mode. The prerequisite for the validity of this conclusion is: ① the analysis object is a DC system and the energy storage adopts constant power control; ② Energy storage can be approximately equivalent to a constant power source/load (depending on the direction of its power reference value), and power does not fluctuate with changes in external dynamic processes, i.e Δ Pdc=0; ③ Suitable for dynamic stability rather than steady-state research.
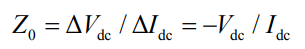
The simplified model is not only able to visually represent the impedance characteristics of battery energy storage, but also mainly used to solve the problem of significant increase in system dynamic order caused by the large-scale development of battery energy storage. It is a trade-off modeling method proposed to address the difficulty of traditional iterative calculation methods or pattern calculation methods in efficiently applying to high dynamic order. It improves computational efficiency and inevitably leads to certain errors. The main reason for the error is the neglect of some dynamic aspects of battery energy storage. At present, research on the error of simplified models for battery energy storage is very limited, because battery energy storage is still in the process of large-scale development and the severity of the error problem has not been highlighted in practical engineering. However, with the development of large-scale energy storage, this will be an inevitable issue, such as pointing out that there are differences between the idealized dynamic response of energy storage control and the actual situation, and this error can lead to incorrect research conclusions. Therefore, the applicable conditions of the simplified model for battery energy storage and the error evaluation and correction methods of the simplified model need to be further explored.
Indeed, research on the stability of DC systems with single battery energy storage connected to the grid has become relatively mature, and a stability mechanism analysis method represented by impedance method has been formed. The instability essence of DC systems has been explained from the perspective of negative impedance, and verification has been conducted based on mode analysis method and time-domain simulation method. However, a clear explanation of the mechanism is based on the neglect of energy storage batteries and the simplification of battery energy storage control. However, the conditions and adaptability of model simplification are currently less concerned, which leads to a lack of solid theoretical basis for whether the mechanism explanation is applicable to any scenario. Therefore, this article provides the following guiding discussion on the applicable conditions of the simplified model for single battery energy storage. Assuming that the input impedance of battery energy storage is Z1 (s) and the input impedance of DC system is Z2 (s) when considering control, the characteristic equation of battery energy storage grid connected system is:
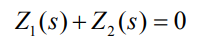
Assuming the input impedance of the simplified battery energy storage model is Z0, the characteristic equation of the simplified battery energy storage grid connected system is:
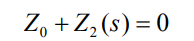
Obviously, for any stability analysis, there must be a target eigenvalue λ = ε + J ω Or target frequency band s c[ ω ,ω ] , Under this condition, the model simplification error can be evaluated using equation (6).
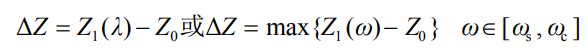
From equation (6), it can be seen that when Z1( λ) = At Z0, the model simplification is error free; When Z1( λ) != When Z0, it represents the consideration of the difference between control and simplification Δ The larger the Z value, the greater the error. It can be seen that the adaptability of the simplified model is closely related to the research object.
Currently, most research on error evaluation methods for simplified models of battery energy storage is based on electromagnetic transient simulation models for time-domain characteristics comparison. This method has a simple approach and can evaluate the accuracy of the simplified model by comparing the similarity of dynamic curves between the simplified model and the accurate model. However, time-domain simulation methods often apply to a specific scenario and parameter set example, and cannot confirm the universality of the simplified model for battery energy storage in general scenarios. To solve this problem, this article provides two ideas: idea 1 is to analyze the impact of model simplification on stability analysis results for specific stability problems, and propose correction methods for stability analysis results; Idea 2 is to break through the modeling itself and propose an accurate equivalent modeling method for battery energy storage for general stability analysis scenarios. The proposed modeling method should be universal in different scenarios. Taking eigenvalue analysis as an example to illustrate idea 1, assuming that the dynamic characteristic equation of the battery energy storage grid connected system is:
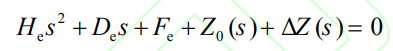
In the formula: G (s)=HeS ^ 2+DeS+Fe is the second-order oscillation link corresponding to the dominant oscillation mode of the battery energy storage grid connected system. Assuming that under the simplified model, He, De, and Fe are constant coefficients, the dominant oscillation mode of the battery energy storage grid connected system is λ E= ε E+j ω e. The error caused by using a simplified model for battery energy storage can be quantified as:
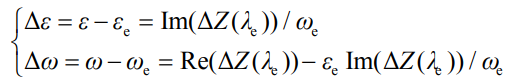
In the formula, Im (-) and Re (-) respectively represent the imaginary and real parts of the variable; Δε 、 Δω The damping calculation error and frequency calculation error caused by the simplified model of battery energy storage are respectively included.
In summary, ignoring the simplified model of batteries and battery energy storage control may lead to misjudgment of the stability of the grid connected system due to error accumulation effects. Therefore, it is necessary to quantify and clarify the simplified conditions and error effects of battery energy storage. Two exploratory solutions are proposed for the simplified model error, in order to provide reference for error evaluation and correction.
2.2 Stability of large-scale grid connected systems for battery energy storage
The large-scale integration of battery energy storage into DC systems mainly includes three access methods: cascade, parallel, and distributed. The schematic diagrams are shown in Figure A5 (a) – (c) of Appendix A. Reference [48-49] studied the control method of DC/DC converter cascade, verified the effectiveness and reliability of cascade control, and constructed the voltage and current relationship between inverters, providing theoretical support for constructing the equivalent impedance of cascade inverters. Similarly, when multiple DC/DC converters are connected in parallel at the same node, their equivalent impedance can also be obtained. Assuming the input impedance of each battery energy storage is Z1 (s), the equivalent input impedance of N battery energy storage cascades is NZ1 (s), and the equivalent input impedance of N battery energy storage parallel connections is Z1 (s)/N. Specifically, the equivalent impedance of multiple energy storage inverters under parallel control was established, and it was concluded that increasing the number of inverters would lead to instability of the DC system, and the number of connections should be limited; The stability problem of DC/DC converter cascade system was studied based on impedance criteria, and improved control was proposed; The impedance determination method has been expanded and a hierarchical stability determination method has been proposed for multi-level DC systems, achieving stability analysis of grid connected systems in specific complex scenarios. Therefore, when multiple batteries are connected to the DC system through cascaded or parallel energy storage, the essence of the large-scale grid connection of battery energy storage leading to the instability of the DC system is no different from that of a single battery energy storage.
However, when considering the general DC network shown in Figure A5 (c) and the significant differences in energy storage among multiple batteries, traditional mode analysis methods are currently mainly used to analyze the impact of different influencing factors on the stability of the DC system based on root trajectory analysis. There is no efficient and accurate universal mechanism analysis method. Another possible mechanism analysis approach was proposed: dividing differentiated battery energy storage into two parts: the same energy storage and different differences, and analyzing the impact of each part on the stability of the DC system to obtain the overall impact of differentiated energy storage. Although this method can to some extent reveal the impact mechanism of different energy storage connections on the stability of the general DC network, there is still significant room for improvement in the accuracy of its evaluation results.
In summary, it can be seen that for large-scale grid connected systems such as cascaded and parallel battery energy storage, existing methods can equivalent it to a single battery energy storage, thus continuing to use its stability analysis method. However, the applicability of model simplification in complex scenarios and the instability factors, risks, and conditions of DC systems in distributed access scenarios for battery energy storage still need to be further studied. The research approach for the stability of large-scale grid connected battery energy storage systems is as follows: starting from the quantity of battery energy storage, starting from the study of a single battery energy storage grid connected system, and then expanding to the stability analysis of grid connected systems with 2, 3, or even multiple battery energy storage. Based on induction, following a path from special to general, gradually generalize the conclusion to complex systems and confirm it. The reason for taking the number of battery energy storage as the starting point is: considering the limitations of stability mechanism analysis methods, as the number of battery energy storage increases, the dynamic order of the grid connected system increases, making it difficult to obtain an analytical solution; Moreover, there is a multi input and multi output interconnection relationship between multiple energy storage and grid connected systems, making traditional impedance analysis methods difficult to apply and stability mechanism analysis methods tend to be scarce. From a single energy storage to two energy storage, although there is only a slight difference in quantity, it is essentially a limitation of the stability mechanism analysis method, which is also the reason for the quantitative separation of a single battery energy storage grid connected system and two or even more battery energy storage grid connected systems.
3.The impact of battery energy storage on the stability of the AC system
Regarding the impact of battery energy storage on the stability of the AC system, the process of mode analysis and impedance analysis introduced in Section 2 is also applicable. As the cumulative effect of error caused by model simplification still objectively exists, this section will not repeat this type of problem, but instead focus on analyzing the new challenges brought by the bidirectional nature of battery energy storage power and the diversity of grid side control in the AC system.
3.1 Stability of a single battery energy storage grid connected system
3.1.1 Grid type battery energy storage
Similar to battery energy storage in DC systems, the stability issues caused by battery energy storage in AC systems are also reflected in two aspects:
① Due to improper tuning of self control parameters and system instability;
② The dynamic interaction between battery energy storage and AC system leads to system instability, which is influenced by factors such as energy storage battery parameters, DC/DC converter control parameters, power flow direction, and DC/AC converter control parameters.
There is currently limited research on the impact of energy storage battery parameters and DC/DC converter control parameters on the stability of grid connected systems. Based on battery discharge experiments, it was concluded that the characteristics of energy storage batteries will change with their service life or appearance environment, resulting in changes in battery parameters. However, no specific analysis was conducted on the impact of relevant changes on the stability of the AC system. A battery energy storage model considering DC/DC converter control was constructed, and the accuracy of the model was verified based on time-domain simulation. In most stability studies of AC systems, energy storage batteries and DC/DC converters are considered as ideal voltage, current, and power sources/loads as a whole. Therefore, the essence of battery energy storage in AC systems is the addition of a constant voltage source and a grid connected converter. For example, by equating energy storage batteries and DC/DC converters as constant voltage sources, the mode analysis method was used to analyze the influence of control parameters of battery energy storage DC/AC grid connected converters on the oscillation mode damping of grid connected systems. It was concluded that a small droop coefficient would have an adverse impact on the stability of the AC system.
Due to the diversity of battery energy storage DC/AC converter control, there are also differences in the conclusions of the impact of battery energy storage on the stability of the AC system under different control strategies. When the grid connected energy storage DC/AC converter adopts a fixed DC voltage control and outputs power to the AC system, the risk and mechanism of instability in the AC system are similar to that of new energy, including instability problems such as phase-locked loop instability caused by weak connections, broadband oscillation caused by negative impedance of resonance points, and sub/super synchronous oscillation caused by strong dynamic interaction between devices. In the above scenario, there is no essential difference in the instability mechanism between battery energy storage and new energy, both of which are stability issues of grid connected inverters. When the grid connected battery energy storage DC/AC converter adopts constant active power control, although the battery energy storage cannot be compared to new energy, there are also stability issues under constant DC voltage control. The stability analysis process can still follow the above method.
In addition, considering the multifunctional control of the DC/AC converter in Figure A2, the impact of battery energy storage on the stability of the AC system is not necessarily negative. There are many literature reports on the positive impact of diversified energy storage control on system stability. For example, literature [59] utilizes the independent active and reactive power regulation ability of energy storage to compensate for system oscillation power through appropriate control strategies, achieving the goal of suppressing low-frequency oscillation; Compensating for the phase locked loop comparison reduces the negative damping effect of the phase-locked loop; A proportional differential feedback strategy for output power has been proposed to effectively suppress sub synchronous resonance in the system. However, the premise for additional control to have a positive impact on system stability is to set the parameters of the additional control reasonably, otherwise it may cause reactions. However, further research is still needed on the selection of additional control parameters.
In addition to control, the power direction of battery energy storage is an important factor that distinguishes it from the stability of new energy sources. The impact of the bidirectional nature of battery energy storage power on the stability of the AC system is shown in Figure 6. Taking the fixed power control shown in Figure 6 (a) as an example: when considering the detailed dynamic process of the battery energy storage grid side converter with fixed power control, regardless of whether the battery energy storage absorbs or emits power, it may exhibit negative impedance characteristics in a specific frequency band. In this scenario, the frequency range of negative impedance that it presents needs to be determined through detailed modeling.
The following is an explanation of the impedance characteristics presented by the battery energy storage connected to the AC system based on the simplified model of constant power control. The simplified model is shown in Figure A6 of Appendix A. The direction of energy storage absorption power is taken as the positive direction, and considering that the AC has two dimensions of d and q axes, the d-axis component of the energy storage input impedance Z0d= Δ Vsd/ Δ Isd, q-axis component Z0q= Δ Vsq/ Δ Isq, where Vsd, Vsq, and Isd, Isq are intersections, respectively
The d and q axis components of current and voltage. Linearize the expressions for active power Ps and reactive power Qs, taking into account that the ideal phase-locked loop has Vsq=0, and the energy storage mainly serves as the support for active power Isq=0, combined with the variation of active and reactive power, is 0, i.e Δ Ps=0 Δ The condition of Qs=0 yields:
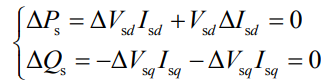
According to equation (9), the d-axis and q-axis components of the input impedance are – Vsd/Isd, i.e. the system impedance Z0dq is:
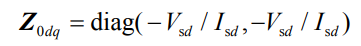
From the above derivation, the following conclusion can be drawn: when the energy storage absorbs power, the pool energy storage exhibits negative impedance; When the energy storage emits power, the battery energy storage exhibits a positive impedance. It is worth mentioning that when battery energy storage is used as a constant power source to supply power to the power grid, it has a positive impedance throughout the entire frequency range and does not cause small interference stability issues. But this does not mean that it will not cause other stability issues, such as static voltage stability issues, transient stability issues, etc. Reference confirmed that the bidirectional nature of battery energy storage power can change its impact on the stability of the AC system by equating battery energy storage under different power flow directions to a constant power source/charge.
Further exploring the stability issues caused by strong dynamic interactions between devices shown in Figure 6 (b), based on the open-loop mode resonance theory, it is assumed that the transfer function between the energy storage of two batteries undergoing strong dynamic interactions is:
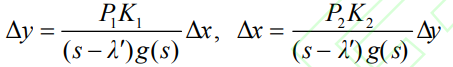
In the equation: Δ X Δ Y is the dynamic interaction variable between the energy storage of two batteries; λ‘ An oscillation mode for battery energy storage; P1 and P2 are the output power of battery energy storage; K1 and K2 are the proportional coefficients of the battery energy storage transfer function; G (s) is the transfer function of the system. The equation in simultaneous equation (11) yields the variation of the eigenvalues Δλ’ For:
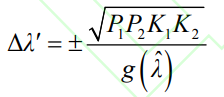
In the equation: ˆλ Is the solution of the two equations in equation (11); Δλˆ= ˆλ – λ’ 。 From equation (12), it can be seen that the change in characteristic values when the power stored by two batteries is in the same direction differs by 90 ° from the change in characteristic values when the power stored by two batteries is in the opposite direction. Therefore, the bidirectional nature of energy storage power will change the impact of battery energy storage on the stability of the AC system.
It should be noted that based solely on the assumption of constant power, the influence of bidirectional energy storage power on stability was simply explored, proving that the influence of bidirectional power is objectively present. When considering the detailed dynamic process of battery energy storage, the correctness of this conclusion needs to be demonstrated in a specific frequency band or for the dominant link. For example, in the context of weak current grids, there is a risk of instability dominated by phase-locked loops in battery energy storage grid connected systems, and the greater the output power or the lower the short-circuit ratio of the grid, the more serious the instability risk is. The dynamic impact of phase-locked loops should be emphasized, and it is not recommended to simply equate battery energy storage with a constant power source/load. However, in the context of a strong power grid, if the impact of phase-locked loops and other dynamic links on the research objectives can be ignored, it can be considered equivalent to a constant power device.
3.1.2 Grid type battery energy storage
When the battery energy storage DC/AC converter adopts grid control, the energy storage battery is generally set as a constant voltage source to provide bidirectional power support capability. The grid type control does not rely on phase-locked loops, so the mechanism of instability of battery energy storage grid connected systems caused by weak connections is no longer applicable. Comparing the impact of weak connections on system stability under grid following and grid building control, it is shown that compared to grid following control, although grid building control has active support ability and can improve the impact of battery energy storage on AC system stability to a certain extent, it still poses a threat to system stability. Although the partial instability mechanism of grid type battery energy storage is different from that of grid type battery energy storage, its stability analysis method is the same. For example, literature [65] based on time-domain simulation concluded that adding virtual inertia control parameters can improve the frequency support ability of energy storage, but will prolong the frequency recovery time, and demonstrated the importance of selecting reasonable control parameters for stabilizing the frequency of the AC system; Reference [66] established open-loop and closed-loop input impedance models for energy storage inverters based on virtual synchronous generator control, indicating that in the frequency band below 0.1 Hz, the closed-loop input impedance exhibits negative resistance characteristics, and further studied its interaction stability with the source side converter; Reference [67] used open-loop mode resonance analysis to verify that the coupling effect between active and reactive power can exacerbate synchronous frequency resonance.
The stability analysis methods for grid type and grid type battery energy storage are similar, but there are certain differences in the conclusions of their impact on the stability of the AC system. The control characteristics of grid type battery energy storage are similar to those of synchronous generators, and the stability problems caused by it are mostly low-frequency oscillations. Furthermore, the mechanism of low-frequency oscillation in the AC system caused by grid type battery energy storage can be divided into the following two aspects. On the one hand, it participates in the dynamic interaction process between synchronous generators in the AC system, thereby triggering low-frequency oscillations between synchronous generators in the AC system. For example, based on the transfer function model of a 2-machine system, the damping torque method was used to elucidate the impact mechanism of virtual synchronous doubly fed fans on low-frequency oscillation of synchronous generators. It was concluded that increasing the virtual inertia time constant and damping coefficient can improve the low-frequency oscillation damping of synchronous generators. On the other hand, it is the low-frequency oscillation caused by dynamic interaction between grid type battery energy storage or grid type battery energy storage and synchronous generator. For example, based on the damping torque method, it was verified that when the open loop modes between energy storage subsystems based on grid control are close, it may lead to rejection of electromechanical oscillation modes in the system, affecting the stability of the system in the electromechanical frequency band; In response to the current limit problem of grid connected operation of energy storage structure grid type inverters and wind turbines with grid type inverters, the complex torque coefficient method is used to derive the active current transmission limit value of the system, and a voltage control method is proposed to improve the transferable active current.
In summary, it can be seen that the impact of battery energy storage on the stability of the AC system changes with different control strategies and power directions, with obvious control diversity and power bidirectional. This is also an important characteristic that distinguishes battery energy storage stability from new energy stability issues. At present, research on the impact of single battery energy storage on the stability of AC systems has been extensive, and traditional stability analysis methods can basically meet the research needs of this stage. However, there is still insufficient research on the mechanism of the impact of diversity in energy storage control and bidirectional power on stability, and further exploration is needed to clarify. Battery energy storage cannot be simply equivalent to a new energy grid connected converter.
3.2 Stability of large-scale grid connected systems for battery energy storage
There are two main ways to connect battery energy storage to the AC system on a large scale: parallel and distributed. The connection diagram is shown in Figure A7 of Appendix A. For parallel connection mode: Multiple battery energy storage can be replaced by a single battery energy storage equivalent based on expansion equivalence, and the stability analysis results are completely consistent with Section 3.1; Alternatively, a parallel energy impedance model can be obtained through grid connected impedance aggregation, which is widely adopted when battery energy storage is the same. Taking multiple parallel power plants as the research object, multiple inverters with the same model and parameters were transformed into one equivalent inverter based on impedance method. The Bode diagram was used to verify that due to the impedance coupling of the power grid, the number of installed inverters has a significant impact on the functionality of the inverters.
When large-scale battery energy storage is distributed and connected to the AC system through multiple nodes, the battery energy storage grid connected system is a multi input multi output system. At this time, the parallel equivalent method fails, and its stability can only be quantitatively evaluated using numerical calculation methods such as mode analysis and generalized impedance method. There is no mechanism analysis method for the stability of large-scale battery energy storage grid connected system. Therefore, existing research usually focuses on two devices or assumes that battery energy storage at different nodes has the same characteristics to simplify the complexity of stability analysis of large-scale battery energy storage systems, revealing the dynamic interaction mechanism between multiple battery energy storage systems from a simple system. For example, by equating N1 grid type inverters to 1 inverter, the dynamic interaction between 2 grid type inverters was studied, indicating that the number and parameters of inverters will affect the stability of the large-scale battery energy storage grid connected system; A study was conducted on the instability mechanism of low-frequency oscillation caused by strong dynamic interaction between any two inverters connected to the AC system, and a parameter tuning method was proposed.
In summary, as the amount of battery energy storage increases, traditional stability mechanism analysis methods will be difficult to apply. When analyzing a single battery energy storage grid connected system, its main characteristics belong to a single input single output system, with low dimensions of dynamic models and mature stability mechanism analysis methods; But when the number of battery energy storage increases to 2, the energy storage between the 2 batteries and the AC system is a multi input multi output system, and the applicable methods are limited to the analysis method based on the generalized Nyquist criterion and the multi input multi output open-loop mode resonance analysis method; As the amount of battery energy storage further increases, the system becomes more complex and lacks analysis methods for its stability mechanism. Therefore, the analysis method for the stability of large-scale grid connection of battery energy storage needs to be researched and broken through.
4.Summary and Outlook
By reviewing and summarizing the impact of battery energy storage access on the stability of AC and DC systems, the following conclusions can be drawn.
1) At present, research on the stability of a single battery energy storage grid connected system is relatively mature, and traditional power system stability mechanism analysis methods can be used. The main reason for instability is the dynamic interaction between battery energy storage and AC/DC systems, and the influencing factors include energy storage battery parameters, power flow direction, and control parameters. However, existing research is usually based on simplified models of battery energy storage, and there is no systematic theoretical proof of their applicability, and there is a lack of error analysis caused by simplified models; The research results on the stability of energy storage control diversity and power bidirectional are not yet sufficient.
2) For the stability of large-scale grid connected battery energy storage systems, existing research mostly equates it to the stability of a single battery energy storage grid connected system, which can be analyzed using mature stability analysis methods. However, the use of simplified models to replace multi-level linkage or consolidation of the Federal Reserve will exacerbate the impact of model simplification errors on the accuracy of stability analysis results, and the cumulative effect of errors is not yet clear; The generalized large-scale grid connected system for battery energy storage has typical multi input and multi output characteristics, which makes traditional stability mechanism analysis methods unsuitable and has not yet been able to reveal the stability mechanism of such complex systems; At present, there is insufficient research on the factors, laws, and conditions that cause instability in grid connected systems under different control, operating conditions, and interconnected networks for large-scale battery energy storage, and attention needs to be paid to them.
Based on the current research status and existing problems mentioned above, future research directions can be mainly divided into the following three aspects.
1) There are two research ideas in the simplification of battery energy storage models: ① for specific stability issues, analyze the impact of model simplification on stability analysis results, and clarify the conditions for model simplification under allowable error conditions. If the conditions for error tolerance are exceeded, additional consideration should be given to the stability error caused by model simplification, and a correction method for stability analysis results should be proposed; ② Propose an accurate equivalent modeling method for battery energy storage for general stability analysis scenarios, and the proposed modeling method should be universal in different scenarios. The first approach can provide evidence to support the effectiveness of model simplification for existing stability research results; The second approach is more suitable for the prospect of large-scale development of battery energy storage, as the stability risks of large-scale energy storage grid connection have not yet been fully explored. Directly adopting a simplified model may lose some risk factors, and precise equivalent modeling methods can provide reliable theoretical support for clarifying the stability risks of large-scale energy storage grid connection.
2) There are two solutions to the problem of traditional stability mechanism analysis methods not being applicable in the large-scale grid connected system of battery energy storage. ① Following the existing technological path, the large-scale battery energy storage is equivalent to a single energy storage, which is simplified as the stability problem of a single battery energy storage grid connected system, and solved based on existing mature stability analysis methods. The dynamic coupling of multiple energy storage systems varies with different conditions, so the key problem to be solved is how to dynamically decouple multiple energy storage systems interconnected by complex networks. Its essence is to achieve equivalent transformation of the dynamic model of the large-scale grid connected battery energy storage system Propose a stability mechanism analysis method for complex systems with multiple inputs and multiple outputs. This can be achieved by expanding the existing stability mechanism analysis methods for single input and single output systems under certain conditions, or by endowing existing stability analysis methods with certain physical significance, making them capable of mechanism interpretation. Its essence is the improvement and innovation of stability analysis theory and methods.
3) The diversity of control and bidirectional power of battery energy storage will significantly increase the complexity of grid connected system stability, and stability analysis results should be gradually improved. Firstly, based on mature stability mechanism analysis methods, the impact mechanism of single battery energy storage on the stability of grid connected systems under different control and power directions is studied; Then, starting from the energy storage of two batteries, analyze the dynamic interaction rules between battery energy storage under different operating conditions and their impact on the stability of grid connected systems, and improve the existing stability analysis results. Only by clarifying the interaction effects and instability mechanisms of the two battery energy storage grid connected systems can there be a theoretical and methodological basis to explore the stability mechanism of general grid connected systems; Finally, explore the potential dynamic interaction instability risks and occurrence conditions between diversified energy storage controls. Obviously, this study is not conducted independently and relies on the precise equivalent model in aspect 1) and the mechanism analysis method in aspect 2). At present, quantitative calculation methods such as pattern analysis and generalized impedance method can be used to analyze the potential instability risks between large-scale battery energy storage in specific scenarios, and the instability mechanism can be traced back based on the analysis results.
