As one of the important sources of clean energy, the grid connected power generation of wind power generation systems is increasing day by day, gradually replacing traditional energy generation systems such as fossil fuels and coal-fired power in certain regions. Although wind energy is widely present in nature, its intermittent and uneven distribution characteristics result in significant fluctuations in the electricity generated by wind power generation systems. Directly dispatching the system’s output power to the power grid system can pose a hidden danger to the overall stability of the power grid. In addition, high power fluctuations in wind power generation systems may cause voltage flicker or frequency changes, which can affect the quality of their grid connection. To avoid these issues, it is necessary to establish appropriate models and technologies to improve the quality of system power generation and power prediction accuracy, and achieve stable scheduling and grid connection of wind power generation systems.
Scholars at home and abroad have conducted extensive research on how to attenuate or smooth the power fluctuations of wind power generation. In order to reduce power fluctuations in wind power generation systems, large energy storage devices are widely used in energy generation systems. Among them, fuel cells and electrolyzers, energy capacitor systems, flywheel energy systems, and battery energy storage systems (BESS) are widely used. On the basis of energy storage systems and wind speed estimation algorithms, Teleke et al. achieved stable power output after attenuating wind energy fluctuations using static synchronous compensators, BESS, and proportional integral (PI) controllers. However, due to the fixed ratio of the PI controller reference signal, this technology can only allocate fixed values of power to the grid. Some scholars have proposed a smooth power scheduling scheme based on fuzzy wavelet transform, but this scheme requires a large capacity BESS to cooperate with the processing of fluctuating power. The grey Markov chain prediction model established by Li et al. has improved the prediction accuracy of random fluctuation data, but the algorithm is relatively complex and has many influencing factors, making it difficult to apply in practice.
Kalman filtering (KF) can be used to estimate wind speed or solar irradiance over a period of time. A fuzzy adaptive Kalman filtering algorithm for wind power generation system management was proposed, but it did not consider the input wind speed in its mathematical model and directly predicted the output power, which is greatly affected by wind speed fluctuations. The wind and solar energy storage and transmission demonstration project launched by State Grid in 2010 achieved the joint application of Kalman filtering algorithm and energy storage system, but it is necessary to ensure that the installed energy storage capacity is not less than 15% of the installed power generation capacity in order to achieve stable grid connection scheduling. At present, most of the research on KF is applied to wind power generation power prediction, and there is little research on accurately estimating the system to grid power generation by simultaneously processing wind speed and power.
In summary, in response to the existing problems of large-scale wind power generation system grid connection scheduling, this article proposes to establish an intelligent predictive scheduling model through battery energy storage system and dual extended Kalman filtering algorithm, using two-step prediction to achieve stable voltage output from the wind power generation system to the superior power grid.
1.Intelligent scheduling model
The Extended Kalman Filter (EKF) algorithm has been optimized on the basis of the classical KF algorithm, solving the problem that the classical KF algorithm cannot handle nonlinear systems. Its core is to perform Taylor expansion on the nonlinear function of the system, preserving the first-order term of the expansion and ignoring the higher-order term, in order to achieve linearization of the nonlinear system. Wind speed and other environmental factors are one of the important factors affecting wind power generation systems, and the variation of wind speed can be regarded as a continuous nonlinear function. Affected by the output results of wind power generation, battery energy storage systems can also be regarded as continuous nonlinear systems. Therefore, the EKF algorithm is selected for predicting the output power of wind power generation systems, and combined with BESS to achieve stable voltage output and intelligent scheduling from wind power stations to the power grid.
The calculation process of the extended Kalman filtering algorithm can be summarized as establishing the system’s state model and measurement equation, and finding the optimal estimation of the system solution based on multiple observations or measurement results. Let Xk be the state variable of the system, and the state equation and measurement equation of the system can be expressed as:
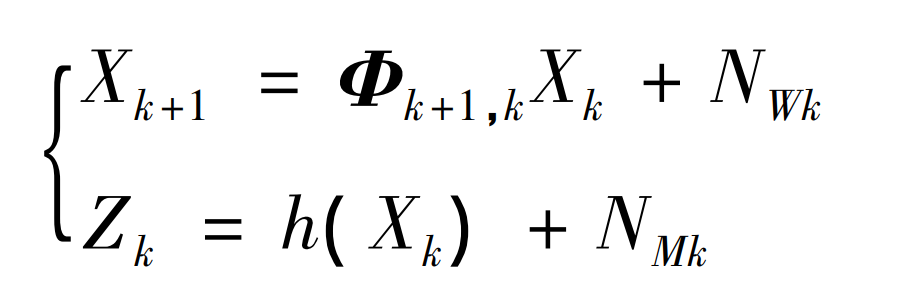
In the formula: subscript k – current iteration steps of the system; Xk – State variable of the current iteration steps of the system; Xk+1- State variable of the system in the next iteration; NWk, NMk – System noise and random noise, calculated using uncorrelated Gaussian white noise, whose covariance matrix can be used ζ K and rk represent; Φ K+1 | k – the state transition matrix of the system; H – Observation model; Zk – System measurement equation.
The EKF calculation process can be mainly divided into two steps, as shown in equations (2) to (6).
One is the prediction of system state and mean square error:
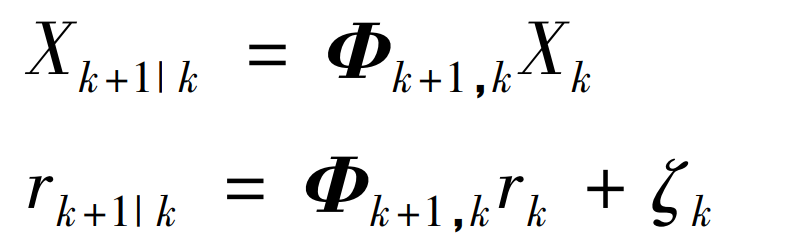
The second is to update the system’s status. The filtering gain of the system is:
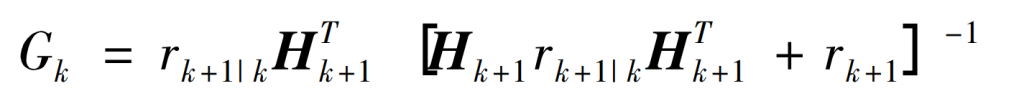
The system state quantity is:
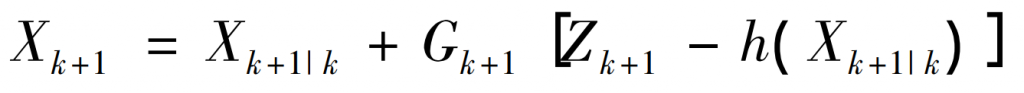
The mean square error of the system is:
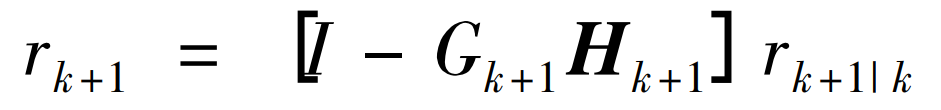
In the formula: Xk+1 | k – the predicted value of the system state; Xk – System state of the previous iteration; Gk – filtering gain; Hk+1 is the measurement matrix used to map state variables to the measurement space.
The calculation process of the intelligent scheduling model based on the extended Kalman filtering algorithm and energy storage system is as follows:
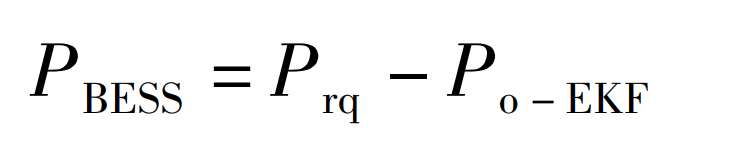
(1) Based on the parameters of the wind power generation system and the mathematical model provided in Section 2 of this article, establish the system state equation;
(2) Set the required output power Prq of the power generation system based on the needs of the superior power grid;
(3) Based on the predicted wind speed value of EKF, calculate the predicted output power Po EKF using the dynamic model provided in Section 2 of this article;
(4) Establish a scheduling model based on the predicted output power and demand output power Prq, analyze the operating mode of the BESS system, and calculate the system’s demand instantaneous power PBESS:
When the output power is less than the required power, PBESS is a positive value, and the BESS system outputs electricity to the grid; When the output power is greater than the required power, PBESS is negative, and the wind power generation system inputs the corresponding power to the BESS system.
Due to the poor robustness of the EKF algorithm, the credibility of the EKF algorithm’s prediction results is poor in complex situations such as system model mismatch, loss of measurement interference, or instantaneous significant changes in measurement. Therefore, using only EKF to predict the output of wind power generation systems can still lead to fluctuations in grid scheduling in extreme cases. To address this issue, it is necessary to continue using the EKF algorithm to estimate the required output power of the battery energy storage system.
(5) Calculate the State of Charge (SOC) of BESS to ensure it is within a reasonable range. This is because accurate SOC can effectively prevent overcharging and discharging of the energy storage system, and improve the service life of the energy storage system. The state of charge of the battery at time t is:
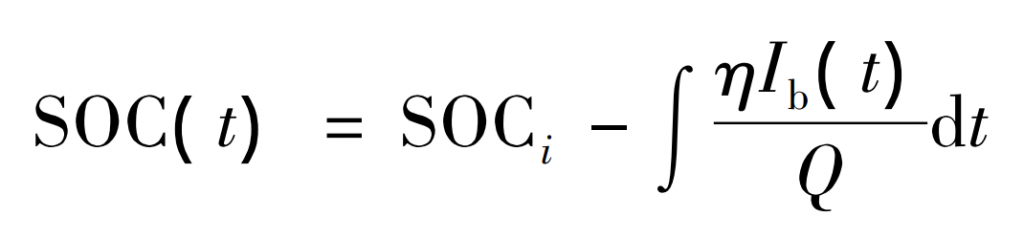
In the formula: SOC (t) – State of charge of the battery at time t; SOCi – Initial state of the battery; Ib (t) – Current at time t, A; Q – Battery capacity, Ah; η— Charging efficiency.
(6) According to the BESS power control model established in Section 2, use the EKF algorithm to predict the required output power of BESS, and the prediction result is PBESS-EKF;
(7) The stable output power Po of the final wind power generation system for overall grid dispatch is:
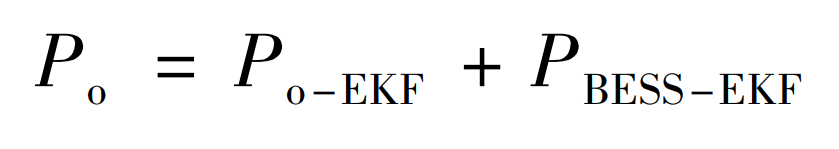
2. Calculation Model
2.1 Mathematical model of wind turbines
Taking the efficient and complex variable speed pitch wind turbine as an example, a control model is established. The changes caused by system parameters are ultimately reflected in the changes in rotor torque Tr and engine torque Tg. When the blade radius is R, the calculation equation is:
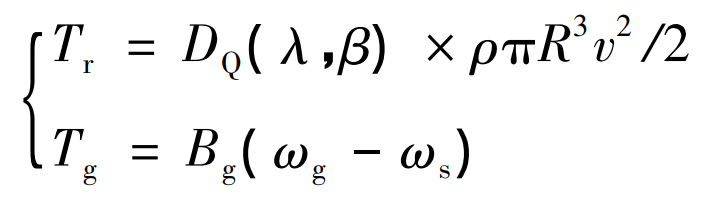
In the formula: DQ – driving coefficient of the wind turbine, and pitch angle β And pitch ratio λ Related; β— Pitch angle, (°); λ— Pitch ratio; V – instantaneous wind speed, m/s; ρ— Air density, kg/m3; Bg – Generator damping, (N · m)/(rad · s); ω G – Generator speed, rad/s; ω S – Fan speed, rad/s.
A dynamic model of a traditional wind power generation system can be established based on system parameters, as shown in Figure 1. The corresponding mathematical model can be described using equation (11).
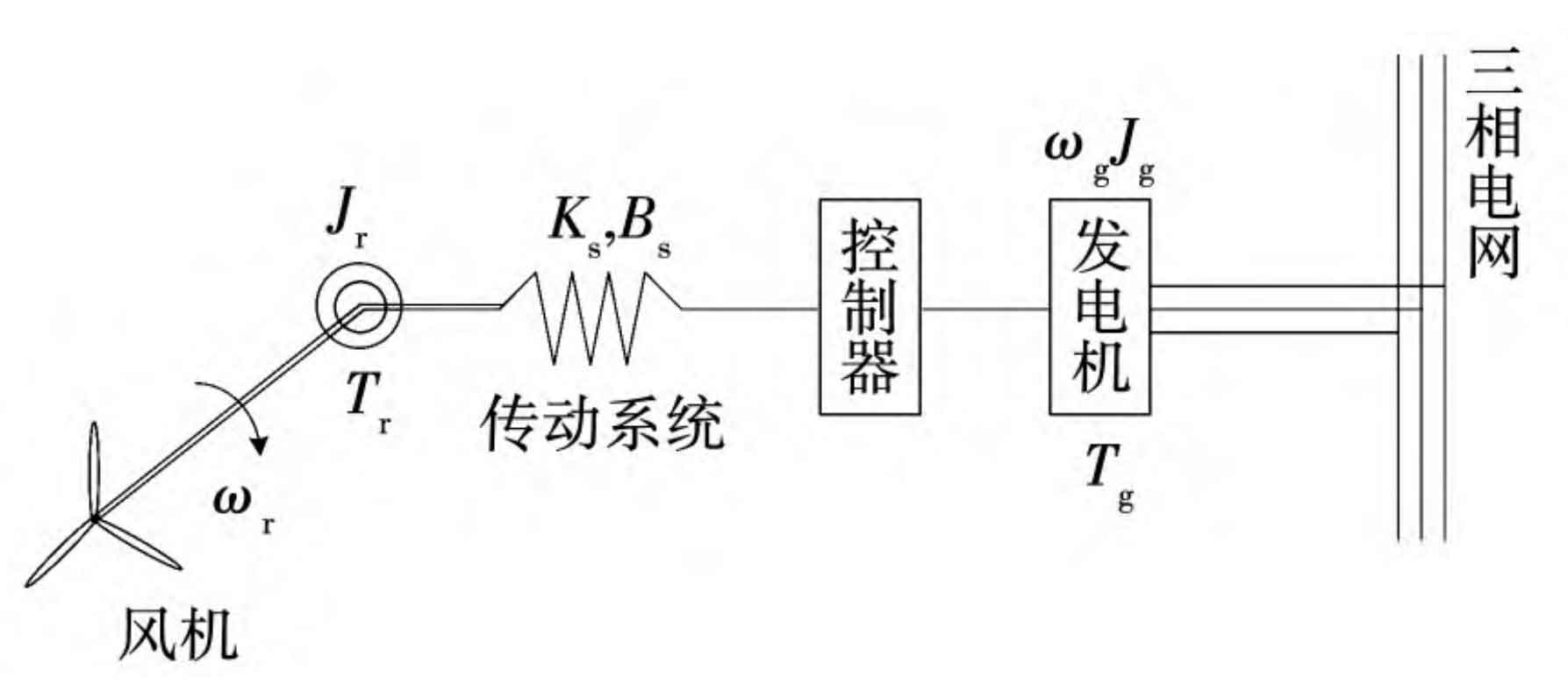
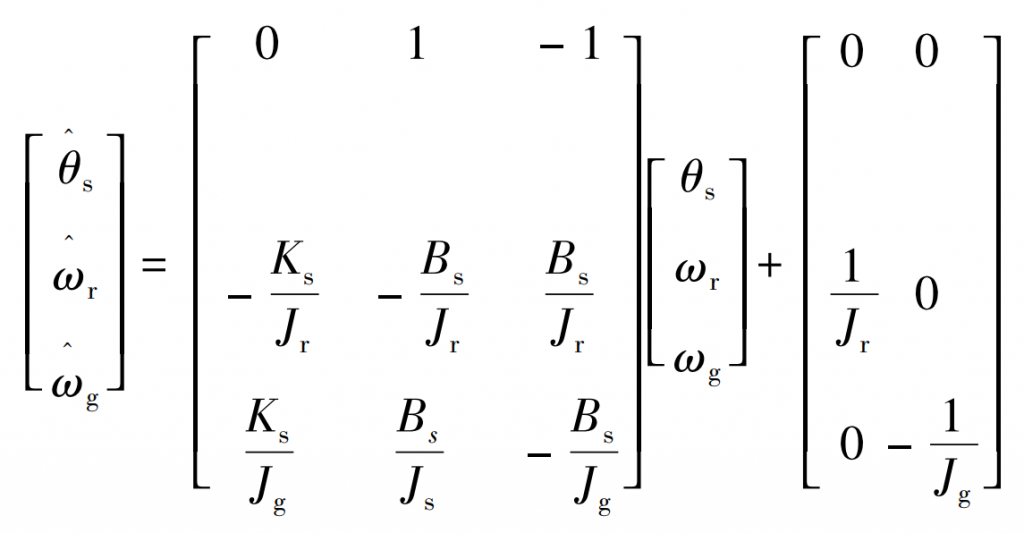
In the equation: ω R, ω G – rotor speed and generator speed, rad/s; ω^ R, ω^ G – estimated rotor speed and generator speed, rad/s; Bs – Damping of the fan transmission system, (N · m)/(rad · s); θ S – Fan angle, (°); θ^— Estimated fan angle, (°); Ks – stiffness of the fan transmission shaft, (N · m)/rad; Jg – Generator inertia, kg · m2; Jr – rotor inertia, kg · m2.
Due to the uncertainty of factors such as wind speed and density, the power output of wind power generation systems is usually nonlinear. It is necessary to control the output power according to the actual situation. In order to calculate instantaneous power, the rotor torque is linearized and estimated based on wind speed, rotor speed, and pitch angle:
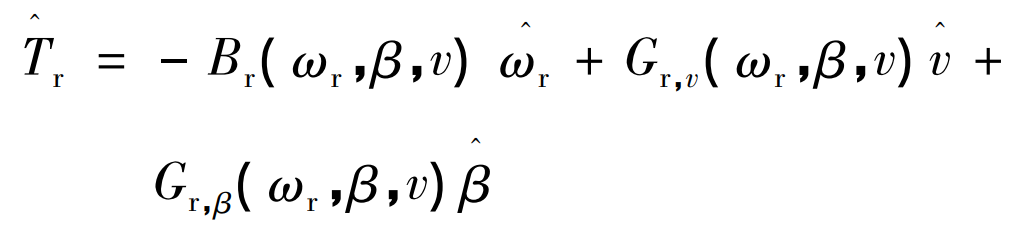
In the formula: T ^ r – estimated rotor torque, N · m; β^— Estimated pitch angle, (°); V – wind speed, m/s; V ^ – estimated wind speed, m/s; Br – linearization coefficient, used to estimate the relationship between rotor torque and speed; Gr, v, and Gr, β— Gain related to rotor torque, wind speed, and pitch angle.
Considering the practical application of the algorithm and the observation period of wind power plants, an appropriate sampling period is selected to discretize the above mathematical state model, making it suitable for the EKF algorithm. The discretized system state and required parameters can be described using equations (13) and (14).
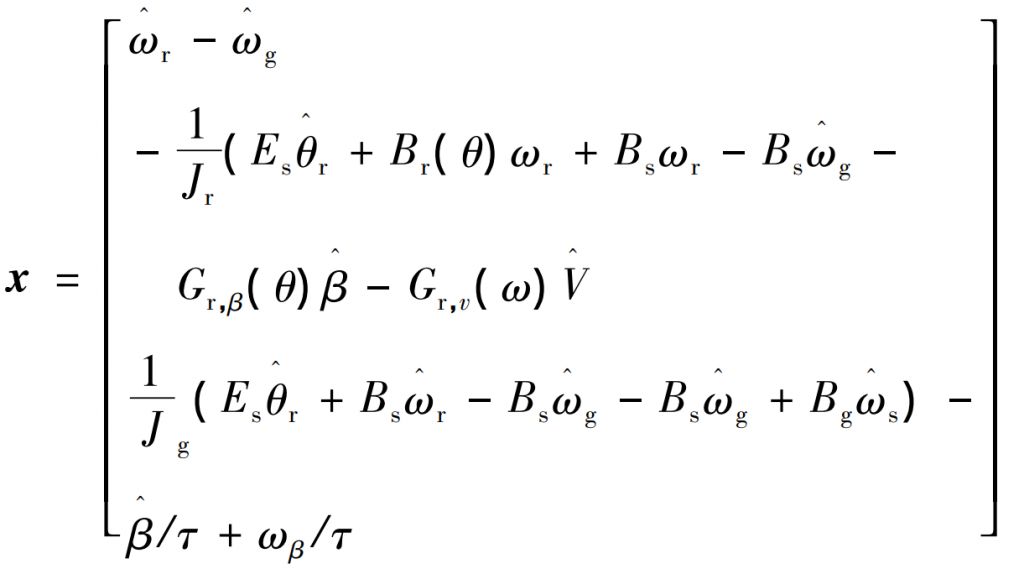
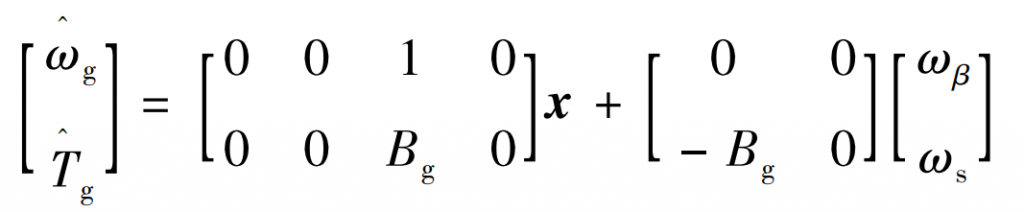
In the formula: x – the state vector of the system; T ^ g – estimated torque of the generator, N · m; E – Elastic coefficient; θ^ R – estimated rotor angle, (°); Br( θ) — Rotor damping coefficient; Bg – damping coefficient of the generator; ωβ— Estimated pitch angle speed, rad/s.
The output power of the power generation system at a certain moment is:
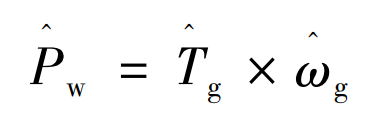
The wind speed v in the model is an uncontrolled nonlinear variable, which is estimated using the EKF algorithm, β D, ω S is the controlled input of the system, obtained through the system controller and sensors. Therefore, based on the observed values, accurate estimation of wind speed can continuously obtain the accurate output power of the system and transmit it as an input parameter to the battery energy storage system.
2.2 Power Control Model of Battery Energy Storage System
BESS configures charging or discharging based on the required power and the output power calculated by the algorithm. When wind power generation is less than the required power, BESS is responsible for providing additional power to the grid. Depending on the capacity and design, the model of the BESS system may not be completely consistent, but a simple first-order resistance capacitance (RC) model can be used to calculate its terminal voltage and current, and then obtain its power for output power estimation using the EKF algorithm.
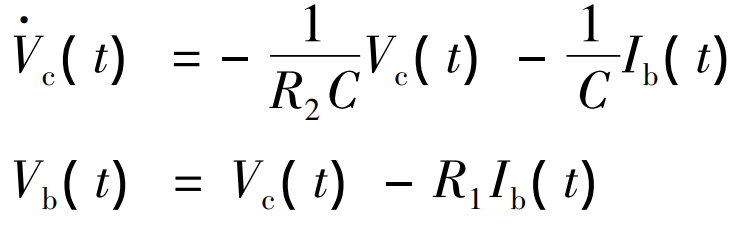
In the formula: Vc (t) – the rate of change of the terminal voltage of the energy storage system with time t; R1- Load resistance, Ω; R2- Internal resistance, Ω; C – Equivalent capacitance, F; Vc (t) – Terminal voltage at time t, V.
Based on the RC model, the battery current Ib (t) and voltage Vb (t) are considered as inputs and outputs of the EKF algorithm, while the capacitor voltage is considered as a state variable of the system, namely:
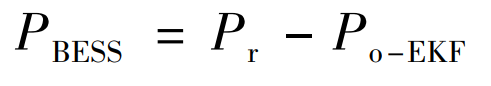
Similar to wind power generation systems, BESS systems use the same sampling period for discretization, and their instantaneous output power can be calculated using the following equation:
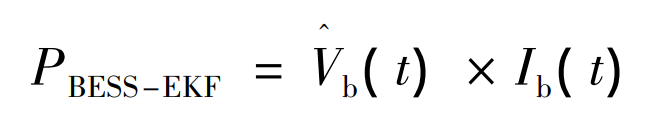
3.Experimental analysis and results
3.1 Impact of Wind Speed on Algorithm Prediction Results
Using the measured wind speed in a certain location in March 2021 as experimental data, the algorithm was simulated and analyzed to verify its effectiveness. The wind power generation system (WPGS) parameters selected in the experiment are shown in Table 1.
| Parameters | Numerical Value |
| Rotor inertia Jr/kg · m ^ 2 | 12428.6 |
| Generator inertia Jg/kg · m ^ 2 | 0.3267 |
| Transmission shaft stiffness Ks/(N · m) · rad ^ -1 | 3.2 × 10^6 |
| Transmission damping Bs/(N · m) · (rad · s) ^ -1 | 1.0 |
| Blade radius r/m | 8 |
| Generator damping Bg/(N · m) · (rad · s) ^ -1 | 1.0 |
| Rotor torque Bg/N · m | 2.0 |
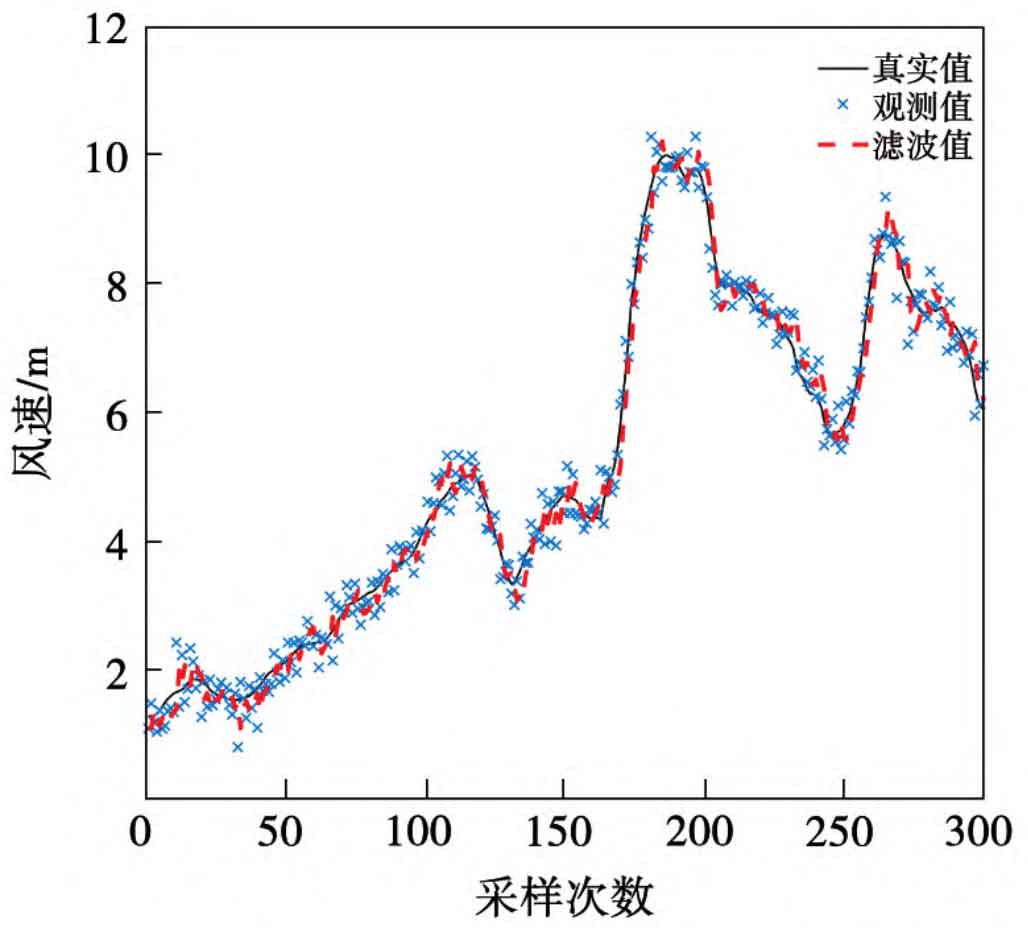
Figure 2 is a schematic diagram of wind speed prediction results. The true value in the figure is the measured wind speed at the location of a certain wind power plant, and the observed value is the observed wind speed provided by the speed measurement module of the power generation system. The sampling period is 15 minutes, and the predicted value is the wind speed prediction result provided by the algorithm in this paper. Table 2 shows the results of some simulation experiments. Through the analysis of experimental results, it can be found that the accuracy of the wind speed prediction value provided by the model in this paper is better than the real-time observation value provided by the sensor, compared to the observation values with systematic errors and large random errors. However, the error of observation values can have a certain impact on the prediction results. Significant outliers can cause fluctuations in the prediction results at the next moment, but they will quickly converge to the true value within 2-3 sampling cycles, ensuring the effectiveness of the algorithm.
| Serial number | True value | Observations | Estimate |
| 1 | 1.27 | 1.21 | 1.2169 |
| 2 | 1.26 | 1.49 | 1.2169 |
| 3 | 1.28 | 1.41 | 1.3884 |
| 4 | 1.30 | 1.17 | 1.4008 |
| 5 | 1.35 | 1.09 | 1.1541 |
| 6 | 1.42 | 1.47 | 1.2089 |
| 7 | 1.49 | 1.18 | 1.3234 |
| 8 | 1.54 | 1.38 | 1.4436 |
| 9 | 1.58 | 1.47 | 1.6045 |
| 10 | 1.62 | 1.84 | 1.5741 |
| 11 | 1.64 | 1.60 | 1.5238 |
| 12 | 1.66 | 1.43 | 1.5094 |
| 13 | 1.68 | 1.56 | 1.6110 |
| 14 | 1.72 | 1.75 | 1.7594 |
| 15 | 1.78 | 1.88 | 1.7788 |
| 16 | 1.82 | 1.87 | 1.7884 |
| 17 | 1.84 | 1.99 | 1.9400 |
| 18 | 1.84 | 1.78 | 1.8350 |
| 19 | 1.83 | 1.90 | 1.8507 |
| 20 | 1.80 | 2.02 | 1.8677 |
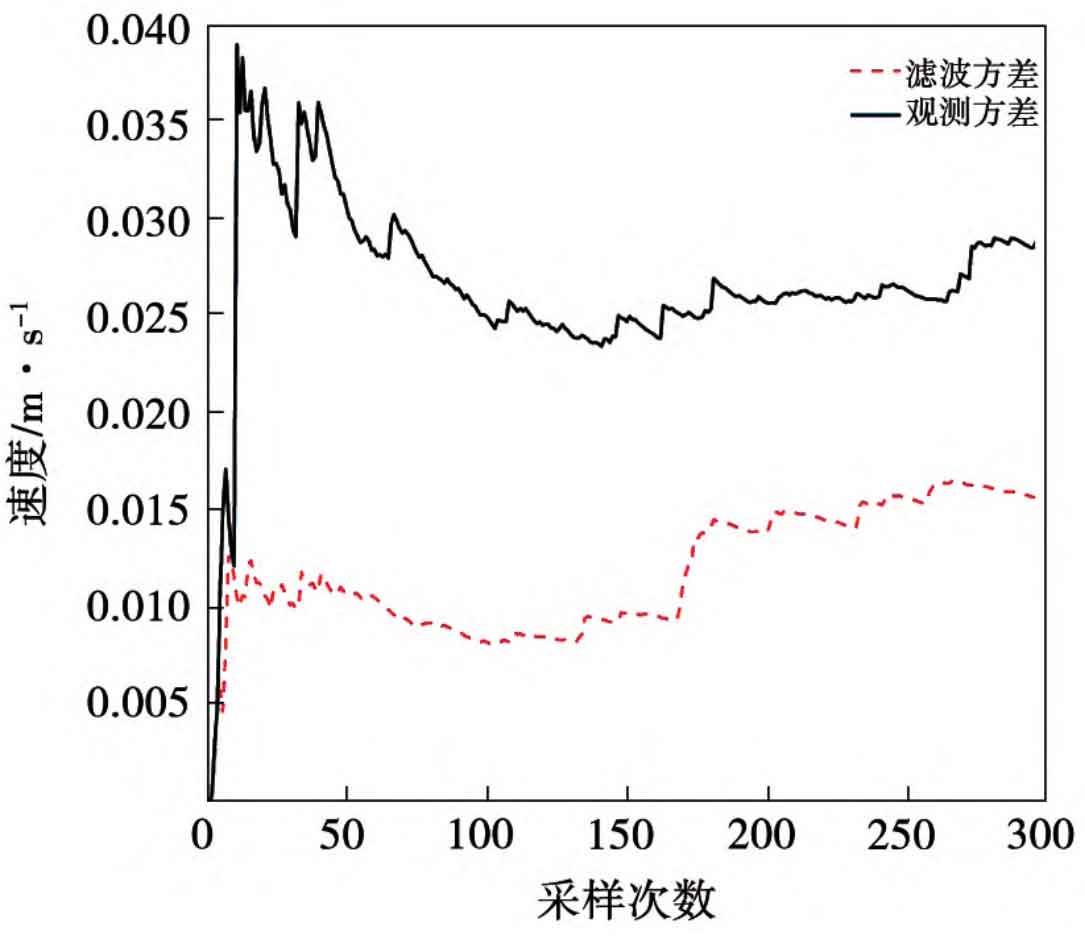
Figures 3 and 4 are schematic diagrams of the variance distribution and error distribution of experimental data results, respectively. By processing the experimental data, it was found that the average error of the predicted wind speed given by the model in this paper is 0.18 m/s, and the average error of the observed values is 0.25 m/s. The variance of the predicted data is reduced by about 45% compared to the observed values. Overall, in situations where wind speed fluctuations are relatively stable, even with significant observation errors, the prediction algorithm can provide wind speed prediction accuracy that is better than 0.03 m/s. When the wind speed fluctuates violently or there are anomalies observed, the prediction algorithm can maintain the accuracy of the current prediction, and can also restore accuracy in a short period of time due to the influence of outliers, which can achieve practical engineering applications.
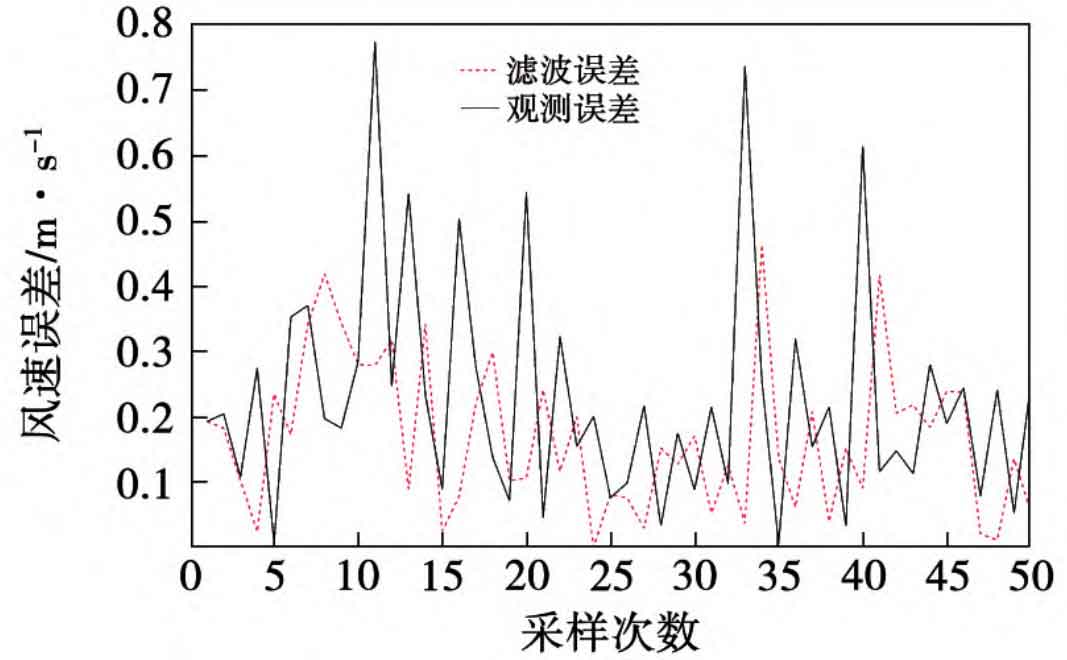
3.2 Prediction of overall system output power
| Parameters | Numerical value |
| Capacitor C/kF | 1 |
| Resistance R1/Ω | 0.02 |
| Resistance R2/MΩ | 10 |
The parameters of the BESS first-order capacitance resistance model used in the simulation are shown in Table 3. Based on this, the overall output power of the power generation system was analyzed. In the simulation analysis, the demand power of the superior power grid was regarded as the reference value, and the power percentage was used to describe the volatility of wind power plants dispatching electricity to the grid.
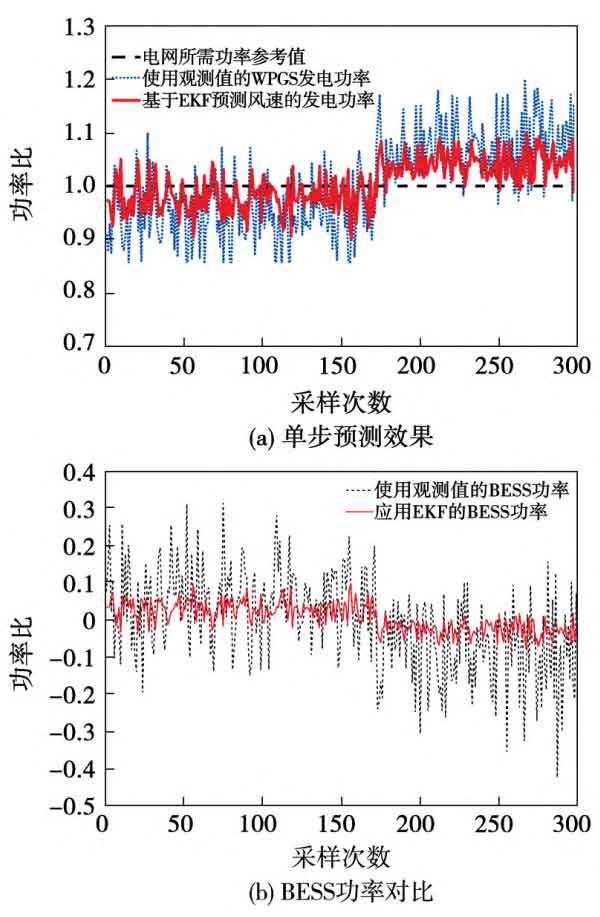
Figure 5 shows the comparison of output power between wind power generation systems and battery energy storage systems. The thick dashed line that is equal to 1 in the figure represents the required power of the power grid. From the analysis of the results in the graph, it can be seen that the power of WPGS and BESS systems using only observed values is extremely unstable, making it difficult to directly output power to the grid. This is due to fluctuations in wind speed and random observation errors. Due to errors in the observed values, fluctuations in the WPGS system can lead to fluctuations in the output and input of the BESS system, resulting in significant fluctuations in the overall output power of the system. Additionally, significant fluctuations in current and voltage can also affect the safety of the battery energy storage system.
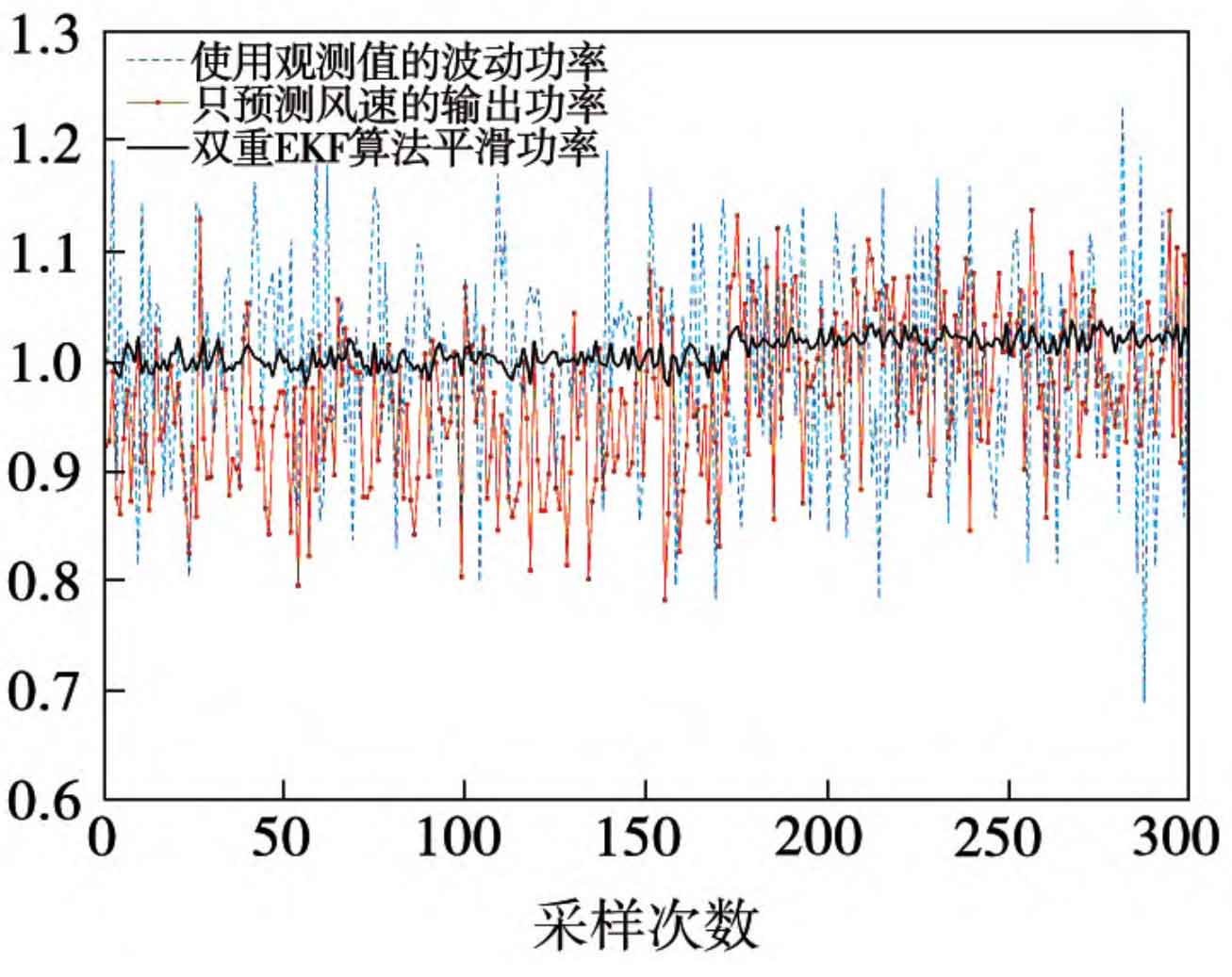
Figure 6 shows the analysis of the overall output power of the system. The thick dashed lines that are equal to 1 in the figure represent the required power of the power grid, while the floating dashed lines represent the predicted power using traditional algorithms. From the figure, it can be seen that the dual EKF algorithm based on the battery energy storage system can ensure the stability of the output voltage. In simulation analysis, the fluctuation of its output power is much smaller than the system power obtained using observation values and traditional algorithms. Compared to the reference power required by the power grid, its fluctuation amplitude does not exceed 2%. Without the use of dual EFK filtering algorithm, the maximum power fluctuation can reach over 20%. The above experimental results indicate that the intelligent scheduling model proposed in this article can achieve stable output from the power generation system to the power grid.
4.Conclusion
This paper proposes an intelligent scheduling technology based on BESS system and dual EKF algorithm to address the potential risks of power dispatch caused by wind speed fluctuations, and conducts experiments on it using measured wind speed and reference power from a certain location. The conclusion drawn from the analysis of the experimental results is as follows:
(1) The algorithm proposed in this article can significantly reduce the impact of random errors and outliers. Compared to the observed values, the measurement error has been reduced by about 35%, and the data variance has been reduced by 45%.
(2) A safety threshold has been set in the BESS output estimation algorithm, which ensures that the error value does not exceed the safety threshold (3% of the reference power) when there are fluctuations in the output of the power generation system.
(3) The proposed scheduling technology can ensure that the wind power generation system outputs electricity smoothly and meets the needs of the superior power grid. The proposed model can ensure that the overall fluctuation of output power does not exceed 2% of the reference power.
