The output of photovoltaic power generation systems has volatility and intermittency, and energy storage systems have important features that can be repeatedly charged, discharged, and recycled multiple times. This can solve the problem of unstable energy supply of solar cell arrays and unstable energy consumption of load circuits due to the fact that photovoltaic power generation is not subject to subjective control and is easily affected by objective factors.
Mainly studied the working principle of photovoltaic energy storage systems and the role of lithium-ion batteries in energy storage systems. By analyzing various types of lithium-ion battery models and comparing their advantages and disadvantages, a second-order RC equivalent circuit model was selected as the basis for SOC research.
1.Working principle of photovoltaic power generation and energy storage system
An independent photovoltaic power generation system consists of a solar cell conversion module, charge and discharge control module, energy storage module, DC load module (or DC/DA converter and AC load), and is a closed loop. Among them, the solar cell conversion module converts light energy into electrical energy; The charging and discharging control module controls the voltage to charge the energy storage module; The energy storage module ensures stable voltage supply to the load module, ensuring the overall stable operation of the system; The load module is divided into two types of circuits: DC and AC. The AC load circuit requires the addition of a DC/DA converter to convert DC into AC.
The energy of the entire photovoltaic power generation system comes from light energy, which is converted into electrical energy through a solar cell conversion module. The energy storage system has the important feature of being able to repeatedly charge and discharge and repeatedly recycle, which can solve the problem of unstable energy supply of solar cell arrays and unstable energy consumption of load circuits caused by non subjective factors in photovoltaic power generation. The energy storage system improves the randomness and instability of the power supply, achieves real-time distribution and power regulation of the entire photovoltaic system, improves scheduling capabilities, and smoothes peaks and valleys. This can maintain system stability and reduce the impact of photovoltaic systems on the power system, improving the controllability of distributed generation output.
The energy storage system provides real-time energy distribution and power control, maintains system stability, and controls the output power of distributed power sources. Therefore, the operational status and energy control of energy storage systems are very important. Chemical energy storage devices are typically used as the primary storage device in energy storage devices for small photovoltaic systems. At present, research on lithium-ion batteries is very active, mainly focusing on the selection of materials for energy carriers and electrodes, energy storage methods, charging and discharging control, balance control, and estimation fields. The working status of the battery and the operation of the entire system can only be judged from the main indicators of the battery – SOC and SOH. Therefore, whether SOC and SOH can be accurately estimated is one of the key research topics in the field of energy storage. The SOC estimation process first requires creating a model of the energy storage device. If the model uses mathematical methods to accurately describe the operating characteristics of the device, the predicted results will also be significantly improved.
2. Structure and operating characteristics of lithium-ion batteries
Lithium ion batteries work by repeatedly embedding and de embedding lithium ions, and are generally defined as secondary batteries that generate current due to the directional movement between the positive and negative electrodes inside the battery. Taking lithium iron phosphate lithium-ion batteries as an example, the reactions that occur during charging and discharging are shown in the following equations.
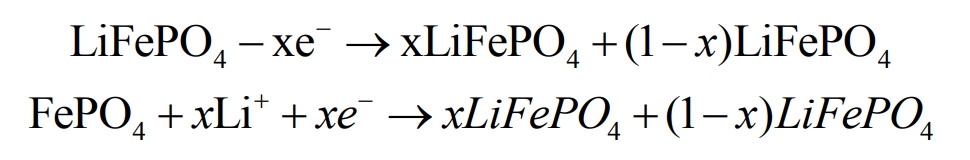
From the electrochemical reaction formula, it can be seen that as the charging and discharging states continue to cycle, lithium ions constantly cycle back and forth between the two poles of the battery, which is the source of charge transfer. When in charging mode, the number of lithium ions embedded in the positive electrode affects the charging capacity of the battery. This relationship can be defined as a positive correlation in mathematics, and the number of lithium ions embedded in the negative electrode during discharge state is also positively correlated with the battery capacity in mathematics. The charging and discharging of a battery are closely related to the electrochemical reaction inside the battery, but the current during charging is positively correlated with the charging rate, and the electrochemical reaction is a process. If the charging rate is too high, the charging capacity may be insufficient. Lithium ion batteries also have environmental temperature requirements, which should be maintained at 0 to 45 degrees Celsius during charging and discharging. If the working environment is at extreme temperatures, the electrode materials of the battery will be irreversibly damaged, the battery capacity will decrease, and the aging process of the battery will be accelerated.
3. Lithium ion battery model
The SOC estimation process requires the establishment of a mathematical model for energy storage devices (lithium-ion batteries). The main purpose of simulating the characteristics exhibited during operation through the established device model is to use mathematical means to describe the complex internal relationships of the battery during operation, thereby reducing difficulty. The mathematical model established by input can achieve highly accurate restoration of the working state characteristics of the battery, and the estimation accuracy of SOC will also be improved accordingly. The mathematical relationship between the inside and outside of the battery can be expressed through the battery model, which can be used to derive the state space equation about the main parameters of the battery and be substituted into the algorithm.
3.1 Empirical Model
The model described by mathematical formulas including battery charging and discharging currents, terminal voltage, internal resistance, SOC, and temperature is generally referred to as an empirical model, and can be simplified based on electrochemistry. There are certain limitations during use.
This is mainly because some parameters of the model are obtained through data fitting under individual operating conditions. Meanwhile, the accuracy and universality of this model are relatively low.
3.2 Electrochemical Model
The electrochemical model mainly utilizes the changes in the number of lithium ions between the positive and negative electrodes, electrolyte, and separator of the battery, focusing on studying the complex reaction processes and mechanisms inside the battery. Use the above changes to describe the characteristics of the battery during operation. Usually described mathematically through electrode reaction equations, potential equations, diffusion equations, and electrochemical reaction equations, this model can fully reflect the reaction process in the battery and has higher accuracy compared to other models (such as thermal models and coupling models).
(1) Single particle model
This model uses two spherical particles to characterize the positive and negative electrodes of the battery. The setting condition is that the concentration of electrolyte remains constant with the internal electrical energy of the battery.
(2) Quasi two-dimensional model
The quasi two-dimensional model is based on countless solid spherical particles to construct the basic composition of lithium-ion batteries and establish a battery model. Use the five parameters of solid phase potential, solid phase concentration, liquid phase potential, liquid phase concentration, and reaction current in the electrochemical reaction process to establish a formula. The quasi two-dimensional model ignores the differences caused by the inherent characteristics of the battery, resulting in a more complex structure and greater computational complexity, and the model parameters cannot be directly measured.
Overall, although electrochemical description of battery models has high accuracy, its complexity is also high, making it difficult to apply. However, the calculation is complex and not suitable for practical applications.
3.3 Neural Network Model
The neural network model uses distributed storage of information and parallel processing of results. It does not include the chemical reactions inside the battery and the dynamic characteristics of the battery during operation. It is essentially a “black box” model that can effectively simulate the nonlinear mapping characteristics between external battery parameters and SOC. This is a complex nonlinear learning model with strong nonlinearity and generalization ability in large sample training sets, while low generalization ability in small sample training sets. Therefore, the model is highly dependent on the training set. An inappropriate training set may lead to overfitting or divergence. If the sample size of the selected training set is large enough, the neural network model can be compatible with different types of batteries through self-learning.
3.4 Equivalent circuit model
The principle of the Equivalent Circuit Model (ECM) is to use circuit components to form a circuit and characterize the relationship between circuit parameters. This method has high accuracy, clear parameters in the model, simple calculation, and is suitable for online estimation.
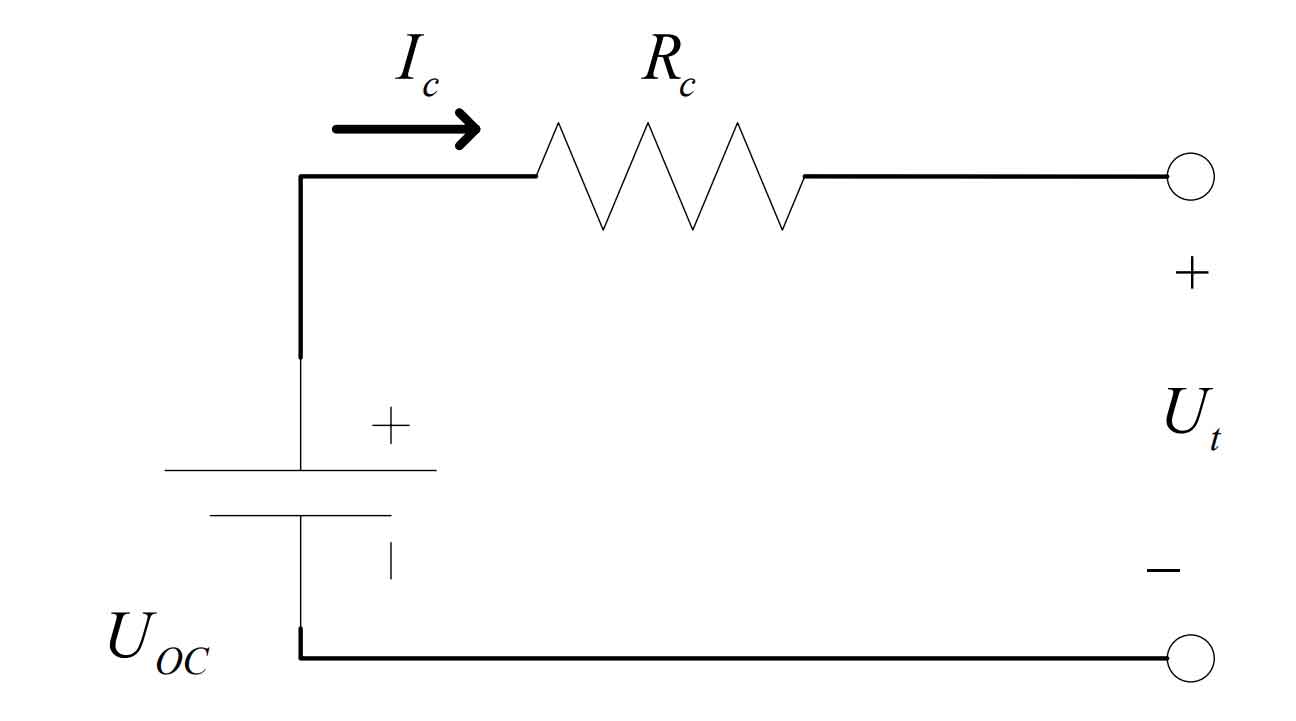
(1) Ohmic Internal Resistance (Rint) Model
The Ohmic internal resistance model is the most basic model, which is connected in series by an open circuit voltage source Uoc and an Ohmic internal resistance R, making it a simple linear model. It has the advantages of simple circuit structure and easy construction of mathematical models. Its disadvantage is that it cannot accurately describe the polarization and aging reactions of the battery during operation, and does not take into account the dynamic changes in battery voltage and resistance during actual operation. As time passes, the accuracy of the model will gradually decrease, and the simulation results and actual values will become too large, which is not suitable for practical work and only suitable for rough estimation of the battery’s state of charge. The Ohmic resistance model is shown in Figure 1.
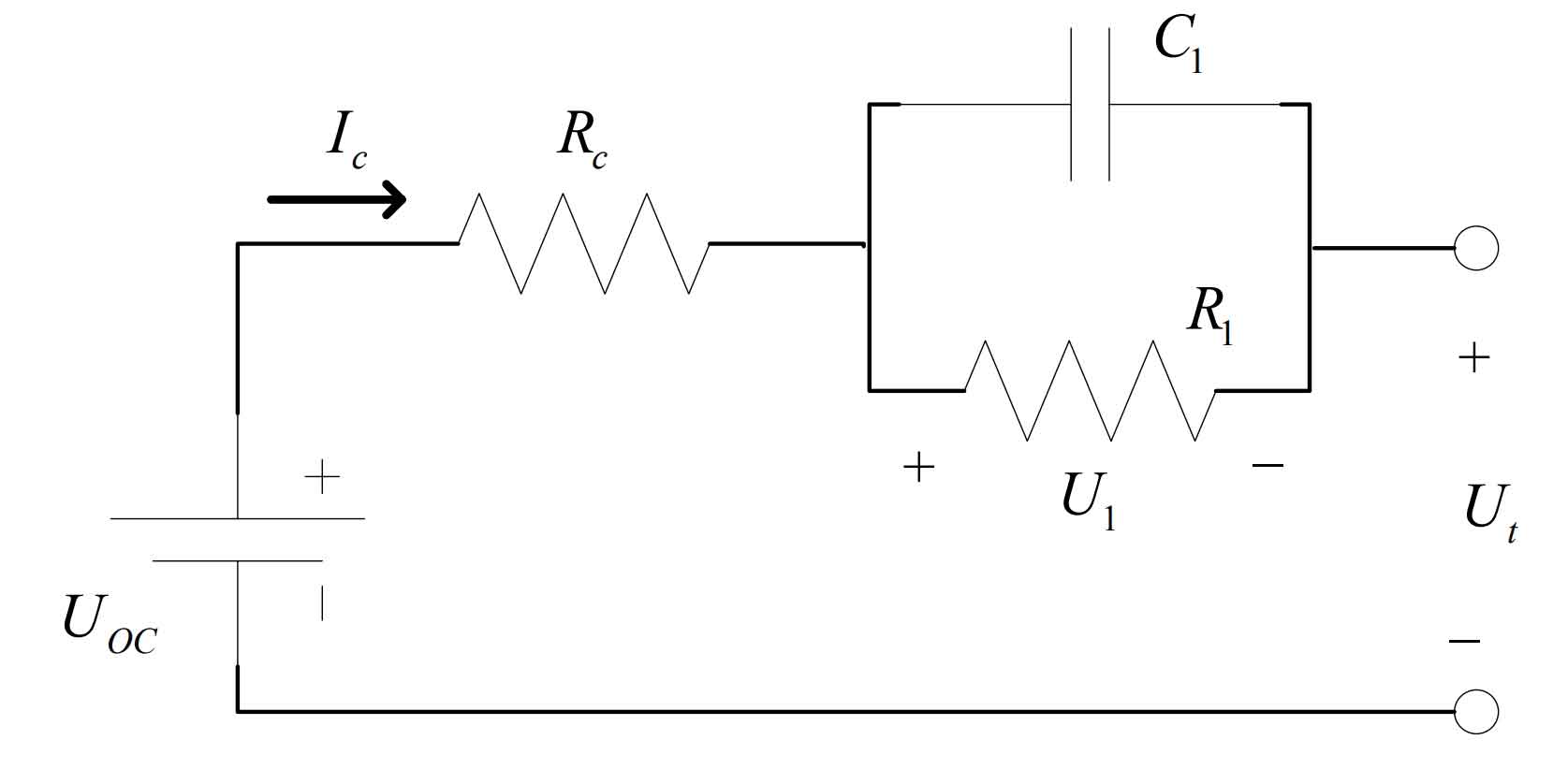
(2) Equivalent Thevenin model
The equivalent Thevenin model has been improved on the basis of the Ohmic battery model and overcomes its shortcomings. Compared with the Ohmic battery model, this model retains the equivalent internal resistance R and adds a set of parallel capacitor resistor structures. Compared with the Ohm battery model, this model can accurately reflect the instantaneous load response of the battery, thereby improving accuracy to some extent. However, this model ignores the steady-state response of the terminal voltage. The model structure is shown in Figure 2.
(3) PNGV model
The PNGV model is a nonlinear battery equivalent model established by adding a series connected capacitor C to the equivalent Thevenin model. This method mainly describes the impact of the accumulation of load current with time on the open-circuit voltage. The newly added series capacitors can maintain high accuracy of the model in the case of rapid changes in current, and can more accurately describe the relationship between SOC and OCV. Compared with the Ohmic resistance model and the equivalent Thevenin model, this model significantly improves accuracy and stability, and the physical meaning of each circuit component is clearer.
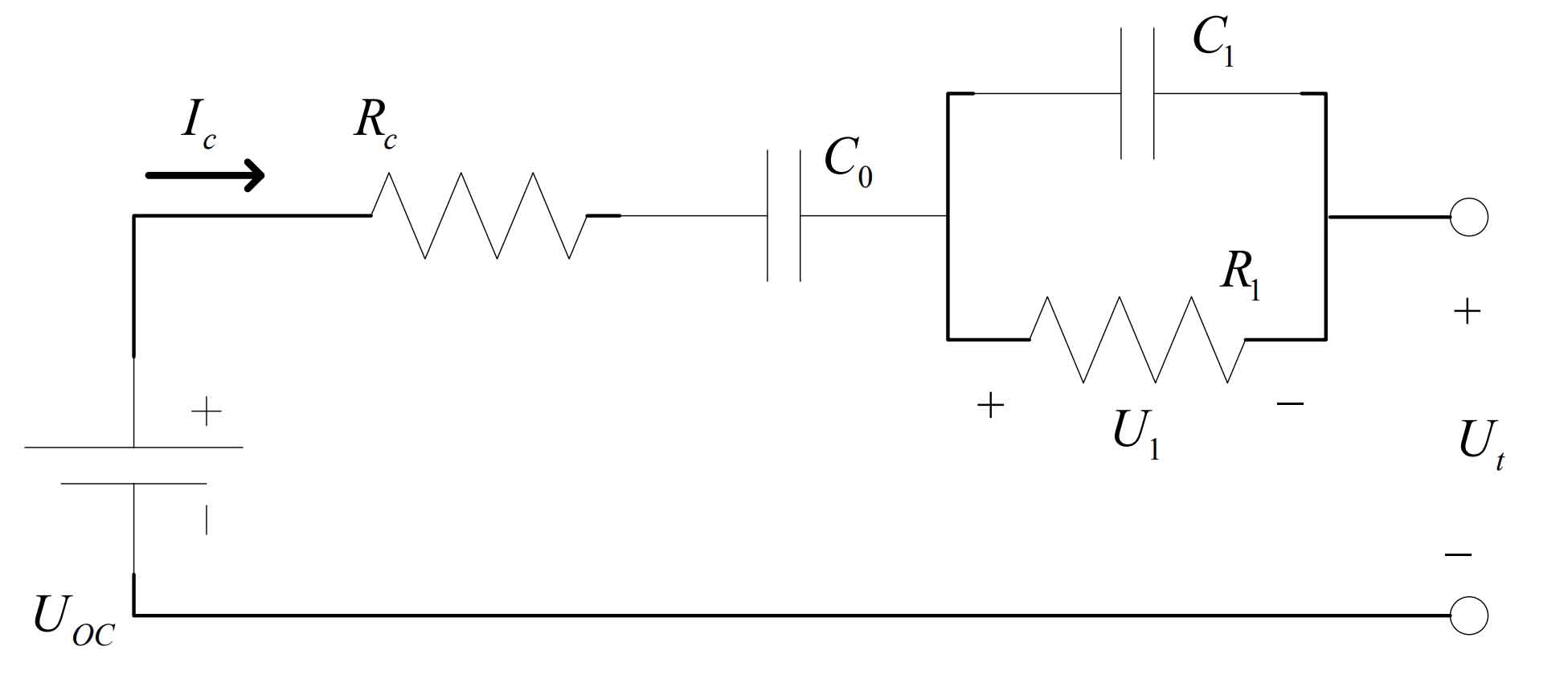
C0 is the equivalent capacitance inside the battery, representing the open circuit voltage change caused by the load current;
UOC is the open circuit voltage of the battery;
RC represents the Ohmic internal resistance of the battery;
The parallel structure of resistor R1 and capacitor C1 has the same effect as the Davining model, used to simulate the polarization process of the battery during use, where R1 is the polarization internal resistance of the battery and C1 is the polarization capacitance.
(4) N-order RC equivalent circuit model
With the continuous deepening of battery model research, circuit models gradually increase open circuit voltage, internal resistance, diffusion effect, and polarization reaction to more accurately describe the working characteristics of batteries and improve the accuracy of battery models. The N-order RC equivalent circuit model is based on the Thevening equivalent model, adding N sets of capacitors and resistance structures. Each set of capacitors and resistance is in parallel to represent the diffusion and polarization effects of the battery. Figure 4 shows the N-order RC equivalent circuit model.
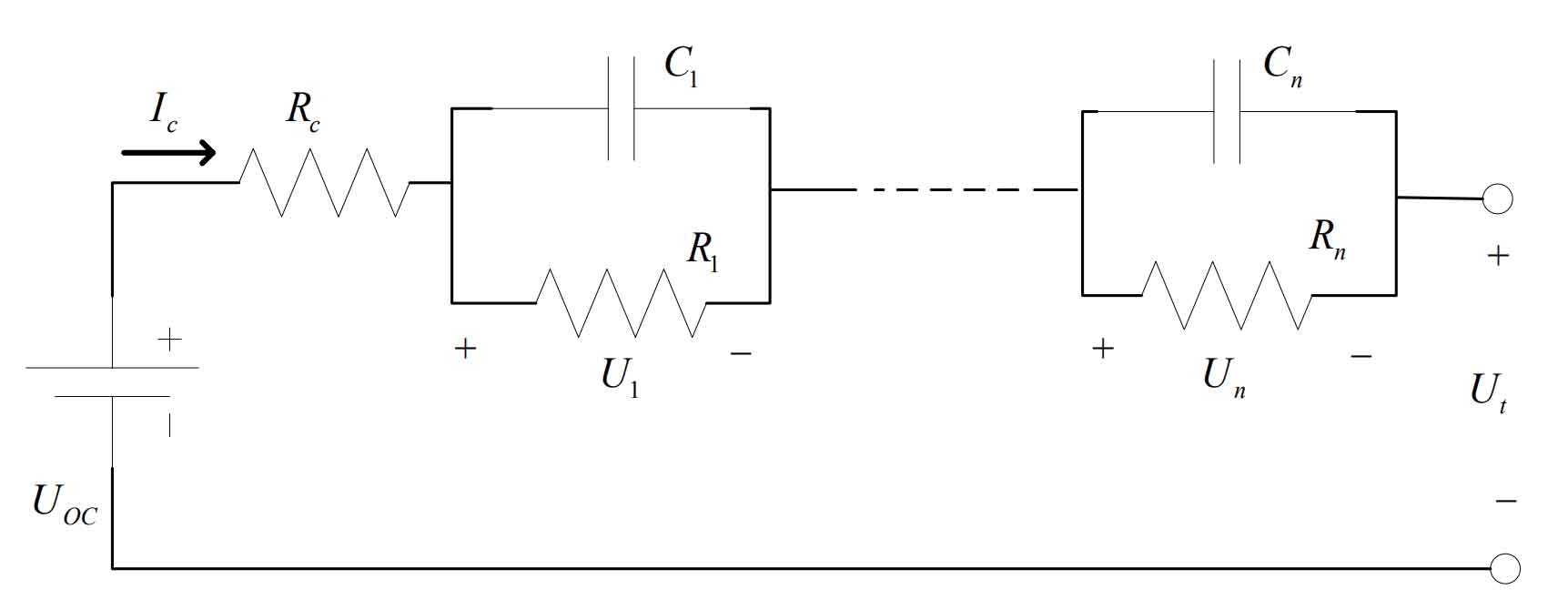
For the N-order RC equivalent circuit model, the higher the RC order, the better the simulation accuracy of the battery model. However, the complexity also increases significantly, and the computational complexity is exponentially positively correlated with the order of N. Although a high-precision battery model can improve the accuracy of the battery, excessive complexity and computational complexity can affect the efficiency of the algorithm. In practical applications, both the accuracy and complexity of the battery must be considered, and an appropriate model order needs to be selected.
From the above analysis, it can be seen that compared with the other three models mentioned above, the N-order RC equivalent circuit model, although slightly more complex in structure, can use mathematical formulas to more highly reproduce the characteristics reflected during battery operation, effectively ensuring the accuracy of the battery. Therefore, there are issues with accuracy and complexity in the constructed model, and it is necessary to maximize the trade-off between the two. In order to achieve better results for both, a second-order RC equivalent circuit model is selected as the model. This model can achieve better results for both, better describe the dynamic changes of the battery, and its effectiveness is far superior to other models. The process of establishing the model will be analyzed in detail in the next section.
4. Factors affecting key parameters of energy storage systems and parameter identification
4.1 Establishment of battery model
The accuracy of SOC prediction and the ability to simulate actual current changes in work depend on the identification accuracy of model parameters. ECM has the advantages of simple structure and good dynamic adaptability. Simulate the polarization effect of batteries using resistors and capacitors in an equivalent circuit model. Due to the higher order of RC, the model becomes more accurate. Research has shown that although the first-order RC model is simple, its model error is somewhat large. However, comparing the second-order RC model with higher-order models, it is found that the error of the second-order model is not significantly different from that of the higher-order model, and its model structure is simple. The structure of this model is more concise and clear, eliminating complex mathematical relationships. The parameters in it can directly represent the specific physical meaning of the components, accurately express the working characteristics, and meet the requirements of stable power supply.
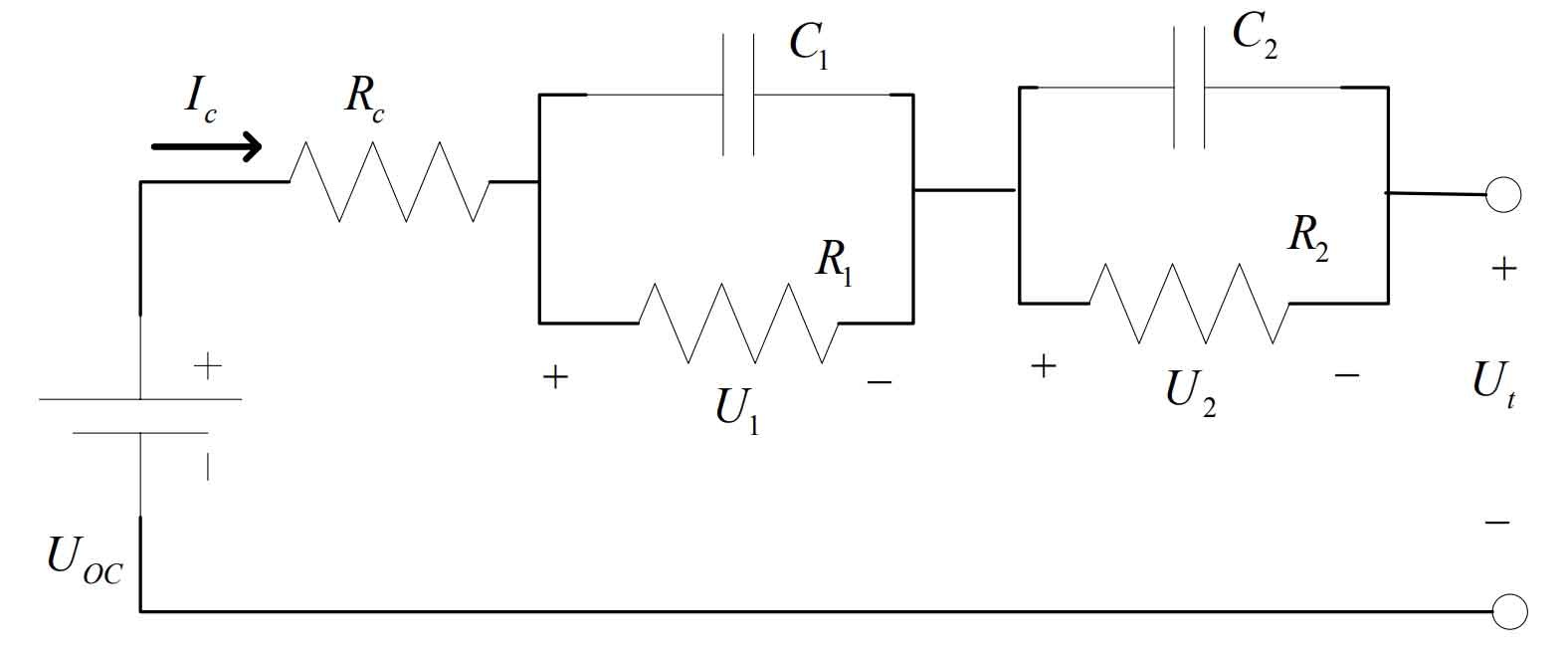
In Figure 5, the second-order RC model includes two sets of RC networks, resistors and voltage sources, with each component connected in series; Ut is the output terminal voltage; UOC is the open circuit voltage of the battery; RC is the ohmic resistance of the battery; CI is the working current of the battery, i.e. the load current; R1 and C1 are the electrochemical polarization resistance and polarization capacitance of the battery, respectively; R2 and C2 are the concentration polarization resistance and polarization capacitance of the battery, respectively.
Using Kirchhoff’s law, it can be obtained that:
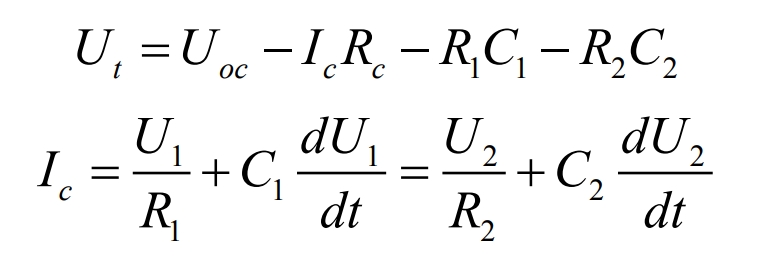
Among them, t is the charging and discharging time, c I is the charging and discharging current, which is positive during charging and negative during discharging.
According to the USCB definition, SOC is the ratio of the remaining capacity of a battery to its nominal capacity at a certain discharge rate, as follows:
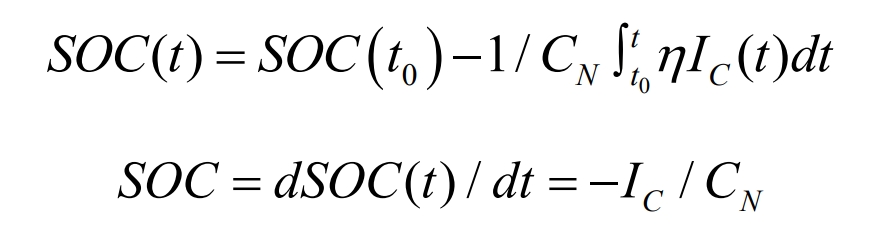
Among them, SOC (t) represents the SOC value at time t, SOC (t0) represents the SOC value at time t, and CN represents the nominal capacity. K represents Coulombic efficiency, which represents the ratio of actual charging current to actual battery current.
According to the open-circuit voltage method, it is known that there is a linear relationship between the voltage source voltage and SOC in the equivalent circuit model. Namely:
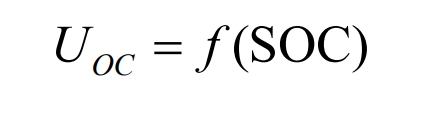
4.2 Battery Model System Identification
The selected single cell battery is NCR-18650GA lithium iron phosphate battery, and the main parameters are shown in Table 1.
| Rated capacity (mA/h) | Typical capacity (mA/h) | Charging cut-off voltage (V) | Discharge cut-off voltage (V) | Nominal voltage (V) | Standard charging current (A) | Charging cut-off voltage (V) |
| 3300 | 3350 | 4.17~4.23 | 2.7 | 3.6 | 1.67 | 4.20±0.03V |
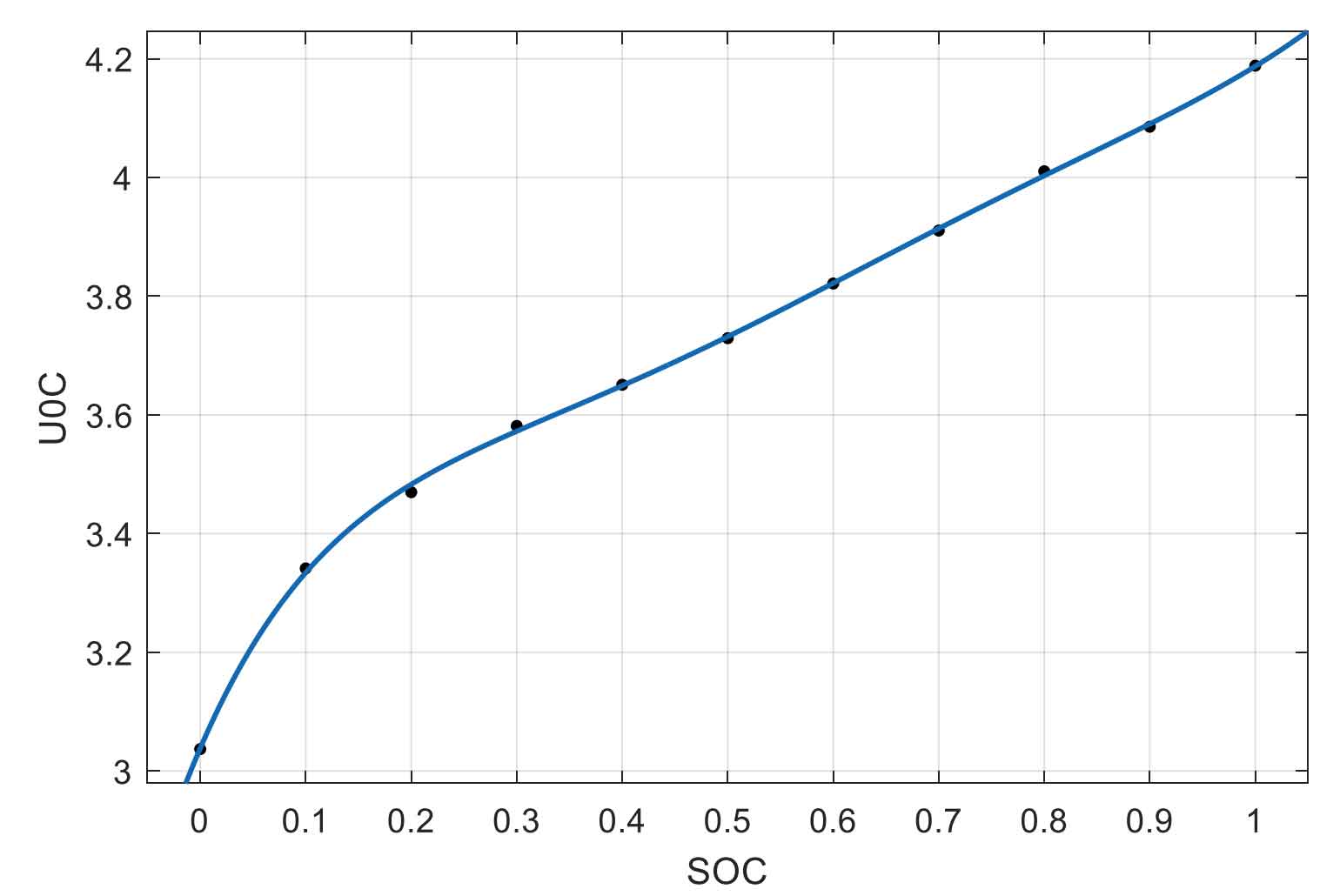
The open circuit voltage OCV is not related to the external structure of the battery, but only to the battery category and other conditions. At a constant temperature, many experiments have shown a clear mapping between the open circuit voltage OCV and SOC of the battery. The values of open circuit voltage OCV and SOC can be obtained by setting specific experiments. The experimental data is shown in Table 2. Experimental data can be used to fit Uoc and SOC to obtain a functional relationship between the two.
| SOC | Uoc |
| 0 | 3.0369 |
| 0.1 | 3.3413 |
| 0.2 | 3.4697 |
| 0.3 | 3.5813 |
| 0.4 | 3.6507 |
| 0.5 | 3.7292 |
| 0.6 | 3.8213 |
| 0.7 | 3.9105 |
| 0.8 | 4.0104 |
| 0.9 | 4.0854 |
| 1.0 | 4.1883 |
The higher the order of the polynomial, the more accurate it is to describe the characteristics of the battery, but its drawback is that the computational complexity also increases significantly. Therefore, considering two factors – accuracy and computational complexity, the experimental data was fitted in the form of a 6-order polynomial using MATLAB software. The fitting curve of the open-circuit voltage with the change of battery SOC is shown in Figure 6.
The fitting function is:
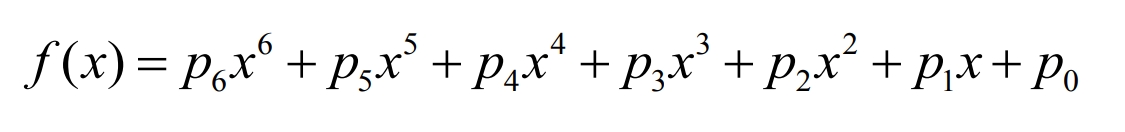
The fitting curve is:
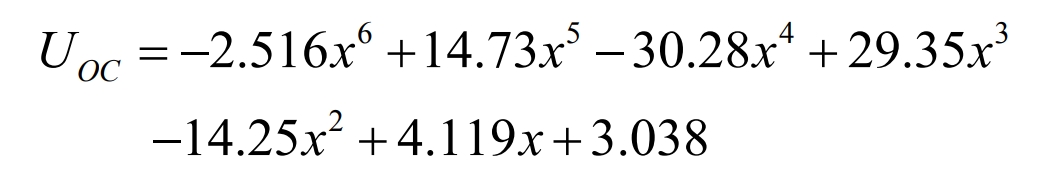
Set the test point interval to 10% SOC value, test the working status of the battery model under different SOC conditions, and record the characteristic parameters. The experimental steps are as follows:
(1) Charge the lithium battery to its full charge state using a constant current constant voltage method. The constant current charging condition charges the battery at 1.67A, and the charging is cut off at a steady-state voltage of 4.2V, with a cut-off current of 0.05A;
(2) Let the battery stand for 1 hour, discharge at a constant current of 1C for 6 minutes, and let it stand for 54 minutes;
(3) Repeat step (2) a total of 9 times, ending.
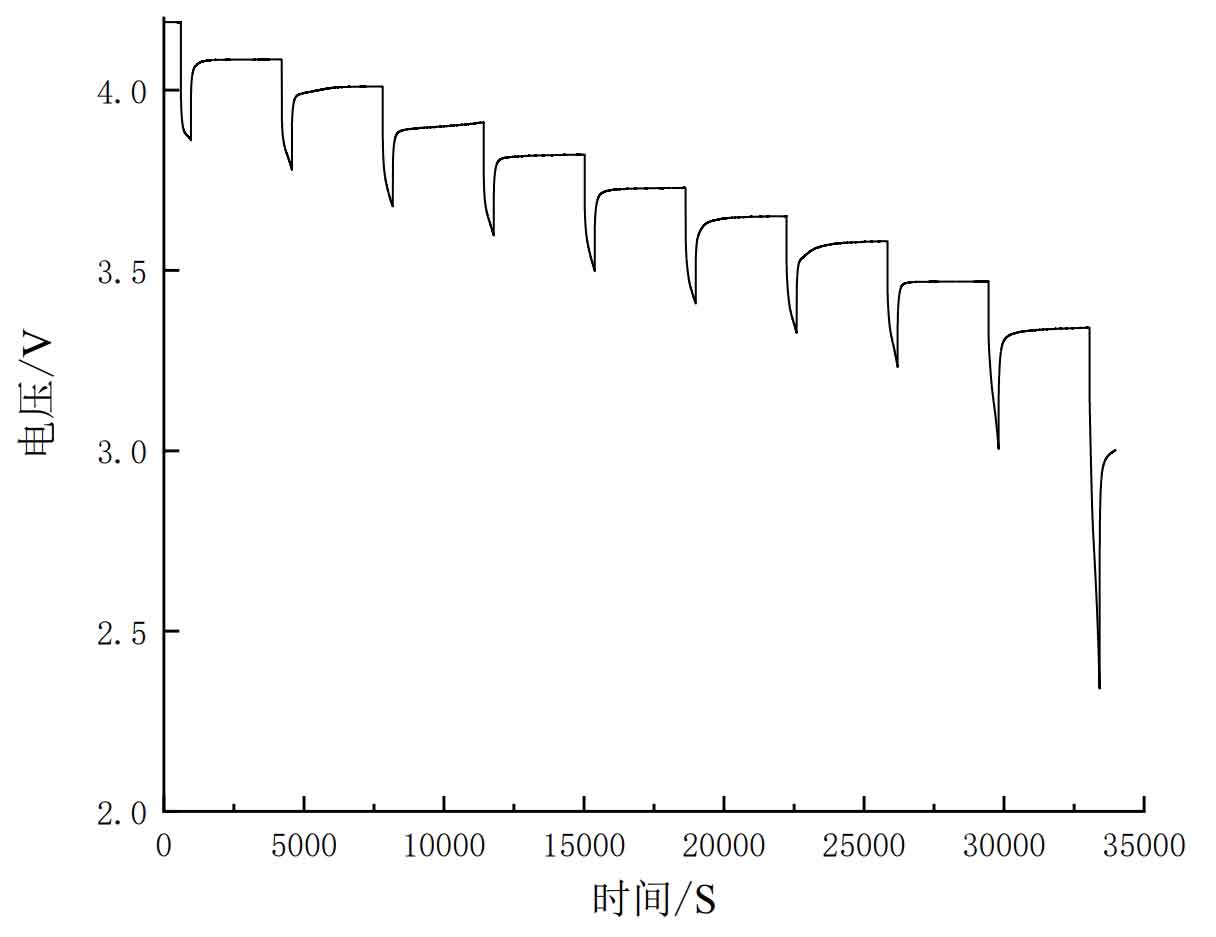
Firstly, a hybrid pulse power characteristic (HPPC) discharge experiment was conducted on the battery. The pulse voltage curve and pulse current are shown in Figures 7 and 8.
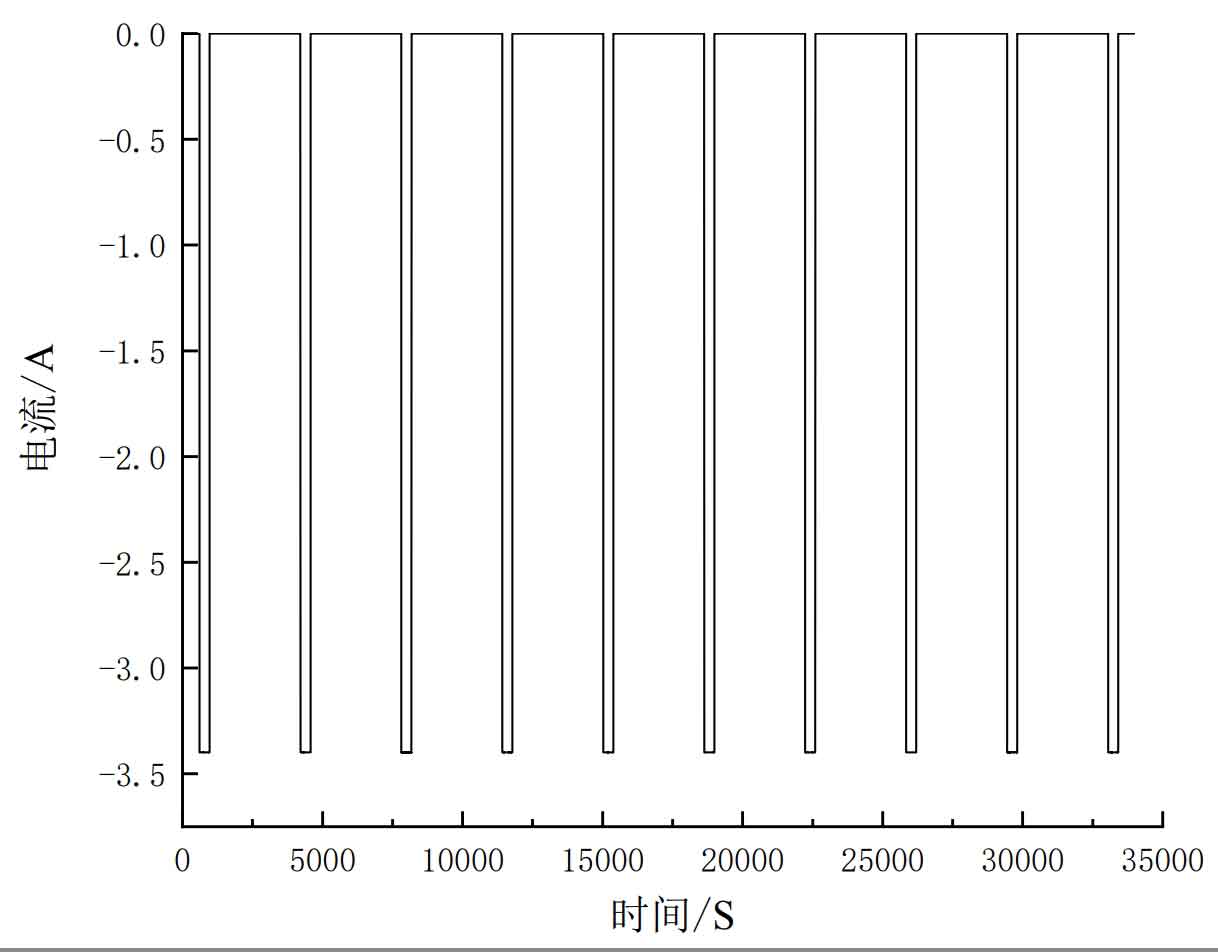
In this article, the MATLAB toolbox was used for the above parameter identification. HPPC tests were conducted at locations with SOC of 1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, and 0, respectively. The obtained parameter values are shown in Table 3.
| SOC | Rc/Ω | R1/Ω | C1/F | R2/Ω | C2/F |
| 1 | 0.0515 | 0.0121 | 326.2 | 0.0081 | 41729.0 |
| 0.9 | 0.0544 | 0.0156 | 8125.1 | 0.0070 | 7621.1 |
| 0.8 | 0.0506 | 0.0147 | 10900.0 | 0.0062 | 13456.0 |
| 0.7 | 0.0531 | 0.0150 | 12437.0 | 0.0057 | 15503.0 |
| 0.6 | 0.0494 | 0.0137 | 9498.8 | 0.0058 | 12180.0 |
| 0.5 | 0.0510 | 0.0147 | 9171.9 | 0.0056 | 13649.0 |
| 0.4 | 0.0538 | 0.0167 | 11358.0 | 0.0057 | 18662.0 |
| 0.3 | 0.0543 | 0.0166 | 13885.0 | 0.0058 | 18704.0 |
| 0.2 | 0.0447 | 0.0111 | 8937.5 | 0.0045 | 12984.0 |
| 0.1 | 0.0783 | 0.0261 | 2164.6 | 0.0085 | 3243.2 |
| 0 | 0.1115 | 0.0270 | 12858.0 | 0.0256 | 5119.6 |
5.Summary
Through analysis of various lithium-ion battery models, it was found that battery models with practical application importance must meet the following requirements:
(1) When establishing a battery model, it is necessary to consider as many practical influencing factors as possible based on the electrochemical reaction principle of lithium-ion batteries, and reflect them in the form of model parameters.
(2) Considering accuracy and complexity, the dynamic and static characteristics of batteries can be more accurately simulated to reflect the response process of SOC to various variables. Meanwhile, the model structure is not very complex. In addition, you do not need to perform too many calculations during use.
(3) By describing the corresponding formula, the physical meaning of each parameter in the formula is clarified, and the corresponding parameters can be accurately identified under existing conditions.
