The integration of renewable energy sources into power grids presents challenges related to intermittency and reliability. Energy storage systems, particularly electrochemical ones, serve as a crucial bridge between generation and load, enabling demand-side management, peak shaving, load smoothing, and ultimately reducing power supply costs. Among these, the battery energy storage system (BESS) has become a focal point of research. However, a significant challenge in deploying BESS is its inherent capacity degradation over time, which critically impacts system performance and operational economics.
This degradation is influenced by multiple factors, including cycle count, depth of discharge, temperature, and critically, the state of charge (SOC) during operation. Extensive research indicates that the SOC operating range profoundly affects the aging characteristics of storage batteries. Batteries cycled within different SOC intervals exhibit markedly different capacity fade rates. For instance, cycles within high SOC ranges tend to accelerate capacity loss compared to cycles within low or mid SOC ranges. Notably, a battery cycled across its full SOC range (e.g., 0-100%) can degrade up to 29 times faster than one cycled within a restricted, partial SOC range. This presents a fundamental operational trade-off: operating a battery within a narrow, low-SOC range can drastically extend its cycle life but requires a larger capacity battery to meet the same energy throughput, increasing capital cost. Conversely, a wider or higher SOC range utilizes the battery’s capacity more fully but shortens its lifespan.
To navigate this trade-off and explore the impact of different SOC operating windows on system scheduling and economics, this work conceptualizes batteries operating within distinct, fixed SOC intervals as different types of storage units within a multi-battery energy storage system. The operational optimization problem for such a hybrid power supply system is then treated as a scheduling problem involving multiple, heterogeneous storage units. This approach allows for strategic dispatch, potentially assigning energy storage tasks to the battery unit whose SOC range offers the most favorable trade between degradation cost and usable capacity for that specific task.
Therefore, with the objective of minimizing the total annual cost of a hybrid power supply system, this paper constructs an operational optimization model for a multi-battery energy storage system based on divided SOC intervals. The model is formulated as a Mixed-Integer Nonlinear Programming (MINLP) problem. A case study of a photovoltaic (PV)-battery hybrid system is used to demonstrate the model’s effectiveness and to analyze how SOC interval division influences optimal power scheduling and overall system economy.
Problem Description
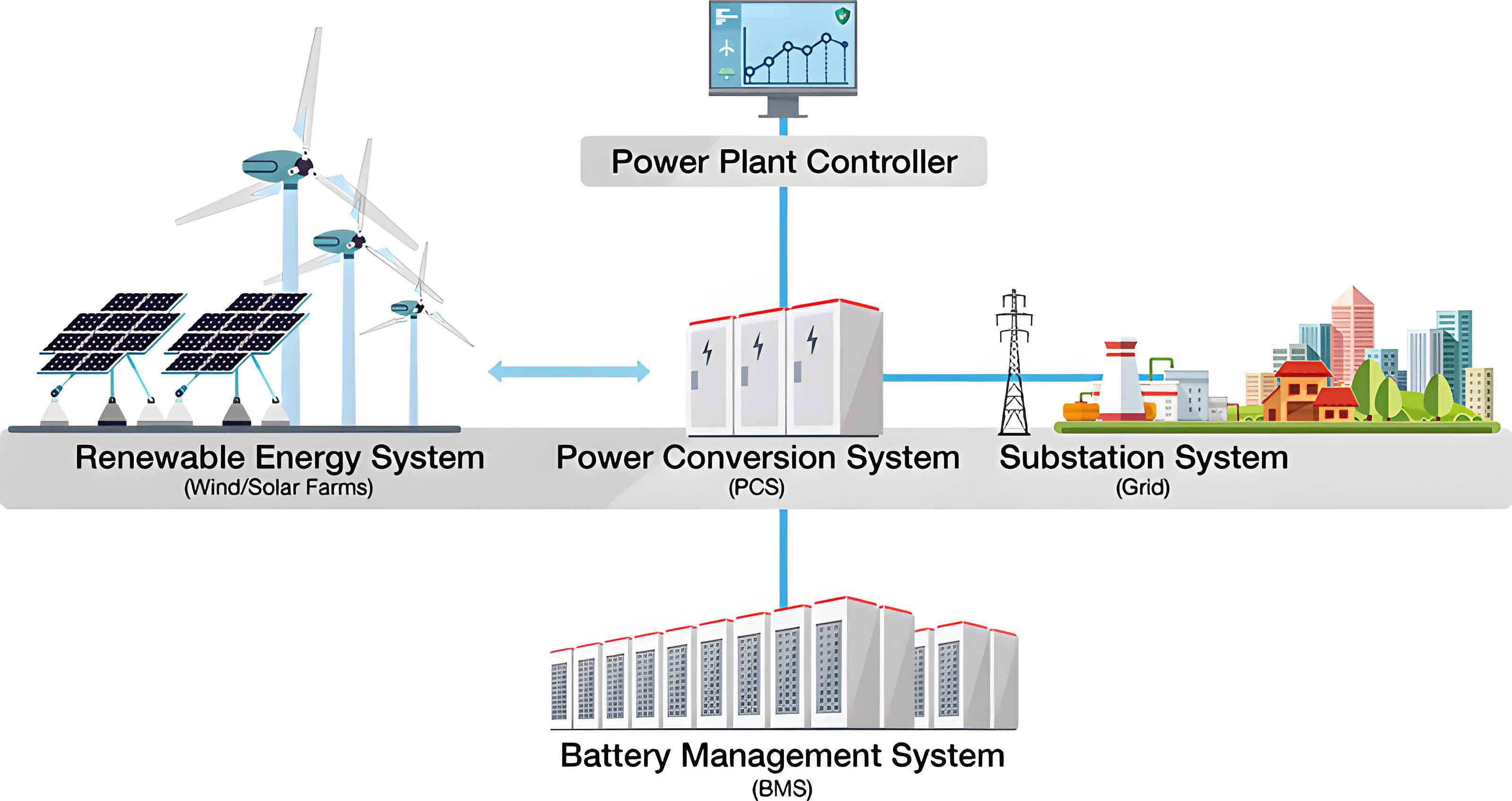
The system under consideration is illustrated in the conceptual diagram above. The hybrid power supply system comprises a PV generation system, a multi-battery energy storage system (BESS), the user load, and the main grid. The BESS itself consists of ‘n’ battery units, each designated to operate strictly within a pre-defined, non-overlapping SOC interval (e.g., low, medium, high).
The PV system can supply power directly to the user, charge the battery units, sell excess power to the grid, or, if necessary, curtail generation. Each battery unit within the BESS can be charged from the PV system or the grid and can discharge to supply the user load or potentially sell power back to the grid, though the latter is often subject to regulations. The core problem is to determine the optimal power flow schedule for all components over a defined period (e.g., one year) to minimize total cost, while explicitly accounting for the unique capacity degradation behavior of each battery unit based on its SOC operating range.
The problem can be formally described with the following known parameters: 1) The PV power generation forecast; 2) The user load demand profile; 3) The configuration (rated capacity, power) and SOC operating limits for each battery unit in the BESS; 4) Other operational and economic parameters, such as charge/discharge efficiencies, electricity prices (for purchase and sale), and battery cost. The goal is to find the optimal operational strategy that minimizes the total cost.
For modeling, we define the following sets:
$N = \{ n \ | \ n \text{ is a battery unit with a distinct SOC interval, } n=1,2,…,N \}$
$K = \{ k \ | \ k \text{ is a time interval, } k=1,2,…,K \}$
where $t_k$ is the duration of time interval $k$.
Optimization Model Formulation
Objective Function
The objective is to minimize the total annual cost $C_{total}$ of the hybrid system, which comprises the cost due to battery degradation and the net operational cost.
$$ \min \ C_{total} = C_{bat} + C_{oper} $$
1. Battery Degradation Cost ($C_{bat}$): This is a capital cost amortization based on the wear incurred during operation. It is calculated for each battery unit based on its capacity loss over the optimization period.
$$ C_{bat} = \sum_{n \in N} \frac{1 – H_{n,K}}{H_{n,ini} – H_{n,end}} \cdot E_{n,rated} \cdot \mu_{n,b} $$
where $H_{n,K}$ is the state of health (SOH) of battery unit $n$ at the end of the period $K$, $H_{n,ini}$ is the initial SOH (typically 1.0), $H_{n,end}$ is the SOH at end-of-life (e.g., 0.8), $E_{n,rated}$ is the rated capacity (kWh) of unit $n$, and $\mu_{n,b}$ is the unit price (\$/kWh) of the usable battery capacity.
2. Operational Cost ($C_{oper}$): This includes operation & maintenance (O&M) costs for the BESS and the net cost of electricity exchanged with the grid.
$$ C_{oper} = \sum_{n \in N} f_{n,inv} \cdot E_{n,rated} \cdot \mu_{n,b} \ – \sum_{k \in K} \mu_{sel} \cdot E_{k,OUT} $$
where $f_{n,inv}$ is a coefficient for the O&M cost of battery unit $n$, $\mu_{sel}$ is the price for selling electricity to the grid (\$/kWh), and $E_{k,OUT}$ is the energy sold to the grid in interval $k$. A purchase cost term from the grid can be added similarly if needed.
Constraints
1. Power Balance Constraints:
PV Generation Balance: PV power can be used to supply demand, charge batteries, be sold, or be curtailed (implied).
$$ P_{k,S} \cdot t_k = P_{k,SD} \cdot t_k + \sum_{n \in N} P_{n,k,SB} \cdot t_k + E_{k,OUT}, \quad \forall k \in K $$
Here, $P_{k,S}$ is PV power output, $P_{k,SD}$ is power from PV to demand, and $P_{n,k,SB}$ is power from PV to charge battery unit $n$.
Demand Balance: User demand must be met by PV and battery discharge.
$$ P_{k,D} \cdot t_k = P_{k,SD} \cdot t_k + \sum_{n \in N} P_{n,k,BD} \cdot t_k, \quad \forall k \in K $$
where $P_{k,D}$ is the load demand and $P_{n,k,BD}$ is the discharge power from battery unit $n$ to the demand.
2. Multi-Battery Energy Storage System Dynamics:
Energy State Evolution: The stored energy in each battery unit updates each period.
$$ E_{n,k,B} = E_{n,k-1,B} + \left( \eta_{n,c} \cdot P_{n,k,SB} – \frac{P_{n,k,BD}}{\eta_{n,d}} \right) \cdot t_k, \quad \forall n \in N, k \in K $$
$E_{n,k,B}$ is the energy stored, $\eta_{n,c}$ and $\eta_{n,d}$ are charge and discharge efficiencies.
Cyclic Boundary Condition: Typically, the schedule is cyclic (e.g., daily, yearly).
$$ E_{n,0} = E_{n,K}, \quad \forall n \in N $$
Capacity Degradation Model: The capacity fade $D_{n,k}$ for unit $n$ in period $k$ is modeled using a cycle-depth-dependent empirical law. A common approach relates degradation per equivalent cycle to the SOC swing ($\Delta S_n$) and mean SOC ($S_{n,m}$).
$$ D_{n,k} = A_{1,n} \cdot S_{n,m} \cdot (1 + A_{2,n} \Delta S_n + A_{3,n} \Delta S_n^2) \cdot \left( \frac{x_{n,k}}{100} \right)^{b_n} $$
The equivalent cycle count $x_{n,k}$ for the period is approximated by:
$$ x_{n,k} = \frac{ \left( \eta_{n,c} \cdot P_{n,k,SB} + \frac{P_{n,k,BD}}{\eta_{n,d}} \right) \cdot t_k}{2 \cdot E_{n,rated}} $$
The parameters $A_{1,n}, A_{2,n}, A_{3,n}, b_n$ are obtained by fitting experimental data for batteries cycled in specific SOC intervals.
State of Health (SOH): The SOH at any point is the initial health minus accumulated degradation. A terminal SOH constraint is enforced.
$$ H_{n,k} = 1 – D_{n,k} $$
$$ 0.8 \leq H_{n,k} \leq 1.0, \quad \forall n \in N, k \in K $$
State of Charge (SOC) Limits: Each battery unit must operate within its designated SOC range.
$$ S_{n,k} = \frac{E_{n,k,B}}{E_{n,rated}} $$
$$ S_{n,min} \leq S_{n,k} \leq S_{n,max}, \quad \forall n \in N, k \in K $$
Charge/Discharge Logic and Power Limits: A binary variable $z_{k,c}$ prevents simultaneous charge and discharge from the entire BESS (can be applied per unit if needed). Power is also limited by rated power and usable energy capacity.
$$ 0 \leq \sum_{n \in N} P_{n,k,SB} \leq z_{k,c} \cdot P_{n,rated} $$
$$ 0 \leq \sum_{n \in N} P_{n,k,BD} \leq (1 – z_{k,c}) \cdot P_{n,rated} $$
$$ 0 \leq P_{n,k,SB} \cdot t_k \leq \min \left( P_{n,rated} \cdot t_k, \ (S_{n,max} – S_{n,min}) \cdot E_{n,rated} \right) $$
$$ 0 \leq P_{n,k,BD} \cdot t_k \leq \min \left( P_{n,rated} \cdot t_k, \ (S_{n,max} – S_{n,min}) \cdot E_{n,rated} \right) $$
The complete model, with variables $J$ in domain $D$, is a MINLP problem:
$$ J = \{ C_{total}, C_{bat}, C_{oper}, P_{k,SD}, P_{n,k,SB}, P_{n,k,BD}, E_{k,OUT}, E_{n,k,B}, S_{n,k}, D_{n,k}, H_{n,k}, x_{n,k}, z_{k,c} \ \forall n,k \} $$
$$ D = \{ J \ | \ \text{Subject to all equations (1) to (19)} \} $$
Case Study: PV-Battery Hybrid System
System Data and Parameters
A residential-scale PV-battery hybrid system is analyzed over a one-year horizon with hourly time intervals ($K=8760$). The PV output and load demand profiles are based on typical meteorological and consumption data. The core of the study involves comparing different configurations of the battery energy storage system.
The battery units are considered to be Lithium Nickel Manganese Cobalt Oxide (NMC) type. Four distinct SOC operating regimes are defined, each corresponding to a virtual “type” of battery unit within the multi-battery energy storage system:
- L-unit: Operates within SOC interval [0.0, 0.2].
- M-unit: Operates within SOC interval [0.2, 0.6].
- H-unit: Operates within SOC interval [0.6, 1.0].
- T-unit: Operates across the full SOC interval [0.0, 1.0].
The key parameters for the battery energy storage system units are listed below:
| Parameter | Value | Unit |
|---|---|---|
| Charge/Discharge Efficiency ($\eta_{c}, \eta_{d}$) | 0.95 | – |
| Rated Power to Capacity Ratio | 1/3 | h$^{-1}$ |
| Unit Capacity Cost ($\mu_b$) | 1595.6 | \$/kWh |
| O&M Cost Coefficient ($f_{inv}$) | 0.01 | – |
| End-of-Life SOH ($H_{end}$) | 0.8 | – |
The degradation model parameters for each battery unit type are derived by fitting the empirical model to experimental cycle life data from literature, which records remaining capacity percentage after a certain number of cycles within specific SOC ranges.
Table 1: Fitted Degradation Model Parameters for Different SOC Intervals
| Battery Unit | $S_{n,m}$ | $\Delta S_n$ | $A_{1,n}$ | $A_{2,n}$ | $A_{3,n}$ | $b_n$ | $R^2$ |
|---|---|---|---|---|---|---|---|
| L (Low) | 0.1 | 0.2 | 4.11858 | 10.84936 | 50.24678 | 0.82851 | 0.98 |
| M (Mid) | 0.4 | 0.4 | 1.80043 | 3.60227 | 7.51058 | 1.02531 | 0.99 |
| H (High) | 0.8 | 0.4 | 1.21842 | 1.60217 | 2.50542 | 1.49401 | 0.96 |
| T (Full) | 0.5 | 1.0 | 0.95271 | 0.77422 | 0.24505 | 1.81234 | 0.97 |
Optimization Results and Discussion
The MINLP model is implemented and solved using the GAMS platform with the SCIP solver. To ensure a fair comparison, the total installed energy storage capacity is kept constant across scenarios. For the multi-battery energy storage system configurations, the sum of the rated capacities of all constituent units equals the capacity of the single full-range (T-unit) system.
1. Economic Comparison: Multi-BESS vs. Single Full-Range BESS
The primary comparison is between a system with a multi-battery energy storage system composed of L, M, and H units (Configuration B-LMH) and a system with a single T-unit battery energy storage system (Configuration B-T).
Table 2: Economic and Degradation Results for Key Configurations
| Configuration | Total Cost (\$) | Degradation Cost (\$) | Operational Cost (\$) | Capacity Fade (%) |
|---|---|---|---|---|
| B-T (Single Full-Range) | 389,432 | 381,500 (97.96%) | 7,932 (2.04%) | 8.8 |
| B-LMH (Multi-BESS) | 305,903 | 281,312 (91.96%) | 24,592 (8.04%) | L:1.6, M:3.8, H:1.6 |
The results are striking. The multi-battery energy storage system (B-LMH) reduces the total annual cost by 21.45% compared to the conventional single full-range battery energy storage system (B-T). This significant saving stems primarily from the drastic reduction in degradation cost ($\Delta C_{bat} \approx 100,188$), which far outweighs the increase in operational cost ($\Delta C_{oper} \approx 16,660$). The T-unit suffers from very high capacity fade (8.8%) due to the stress of cycling across its entire SOC range, leading to a dominating degradation cost. In contrast, the partitioned operation in the multi-battery energy storage system confines each unit to a less stressful SOC range, dramatically slowing down capacity fade, especially for the L and H units.
2. Operational Dispatch and Battery Utilization
Analyzing the optimal power dispatch reveals how the multi-battery energy storage system manager intelligently utilizes the different units. All three units (L, M, H) participate in charging and discharging cycles throughout the year. However, their utilization levels differ significantly. The M-unit handles the largest share of the energy throughput, followed by the H-unit and then the L-unit. The dispatch priority effectively becomes L > M > H. This scheduling logic emerges from the optimizer’s trade-off between the usable energy window $(S_{max}-S_{min}) \cdot E_{rated}$ and the degradation cost per cycle for each unit. The M-unit offers a good balance: a larger usable capacity than the L-unit and a slower degradation rate per equivalent cycle than the H-unit for the relevant number of cycles experienced in this annual schedule.
The SOC trajectories confirm that each unit in the multi-battery energy storage system operates strictly within its designated bounds (e.g., L between 0-0.2, M between 0.2-0.6, H between 0.6-1.0), while the T-unit’s SOC swings widely from near-minimum to near-maximum. This constrained operation is the key to extending battery life within the multi-battery energy storage system framework.
3. Impact of Different Multi-BESS Compositions
To further understand the economics, various compositions of the battery energy storage system are evaluated. The total cost, degradation cost, and operational cost for different combinations are summarized below.
Table 3: Cost Analysis for Different BESS Compositions (Equal Total Capacity)
| BESS Configuration | Total Cost (\$) | Degradation Cost (\$) | Operational Cost (\$) |
|---|---|---|---|
| B-T (Full-Range only) | 389,432 | 381,501 | 7,932 |
| B-L (Low only) | 319,961 | 280,924 | 39,037 |
| B-M (Mid only) | 338,585 | 318,548 | 20,037 |
| B-H (High only) | 286,356 | 264,433 | 21,924* |
| B-LM (Low + Mid) | 326,291 | 299,916 | 26,375 |
| B-LH (Low + High) | 287,719 | 260,086 | 27,634 |
| B-MH (Mid + High) | 307,883 | 286,903 | 20,980 |
| B-LMH (All three) | 305,903 | 281,312 | 24,592 |
*Operational cost for B-H is adjusted for consistency with other single-unit scenarios where total capacity is equalized.
Several insights can be drawn:
- Superiority of Partitioned Systems: Every configuration using partitioned SOC ranges (B-L, B-M, B-H, and their combinations) has a lower total cost than the full-range B-T system. This unequivocally demonstrates the economic benefit of avoiding full-range cycling in a battery energy storage system.
- Role of the H-unit: Interestingly, the single H-unit system (B-H) shows the lowest total cost among single-partition systems. This is because, for the annual cycle count in this specific scenario, the H-unit’s degradation is not yet in its accelerated phase, and its larger usable capacity (compared to L-unit) leads to lower operational costs related to meeting the load.
- Diminishing Returns with More Units: The three-unit system (B-LMH) does not yield the absolute lowest cost. The two-unit system B-LH has a slightly lower cost. This indicates that the number of SOC intervals (or battery unit types) in a multi-battery energy storage system is not simply “the more, the better.” There is an optimal composition that balances the degradation characteristics and the operational flexibility of each unit. Adding more units increases scheduling complexity and may not provide sufficient marginal benefit to justify potential increases in operational constraints or fixed O&M costs.
- Trade-off is Key: The optimal configuration arises from a nuanced trade-off. The L-unit has very low degradation but a small energy window, leading to higher operational costs if used alone. The H-unit has a larger window but faster degradation under high cycle counts. The M-unit offers a compromise. A multi-battery energy storage system allows the optimizer to dynamically assign tasks to the most cost-effective unit at any given time, minimizing the system-wide objective.
Conclusion
This work addresses the critical issue of battery degradation in the economic operation of hybrid power systems. By recognizing the profound impact of the SOC operating range on battery cycle life, I propose and model a novel multi-battery energy storage system framework where the overall storage bank is composed of distinct units, each constrained to operate within a specific, non-overlapping SOC interval.
The formulated MINLP model successfully optimizes the dispatch for such a system, minimizing total cost which includes explicit battery degradation costs based on interval-specific aging models. The case study of a PV-battery system provides clear and robust evidence:
- A multi-battery energy storage system operating on the principle of SOC interval division can achieve significant economic savings compared to a conventional battery energy storage system cycling over its full range. The demonstrated reduction in total annual cost was over 21%, primarily due to drastically reduced capacity fade.
- The operational strategy intelligently dispatches power, favoring battery units whose SOC range offers the most favorable economic trade-off between degradation cost and usable energy capacity for the required service. In the analyzed case, the mid-SOC range unit was most heavily utilized.
- The composition of the multi-battery energy storage system (i.e., the number and choice of SOC intervals) is itself an important design variable. The results show diminishing returns with an increasing number of units, indicating that an optimal configuration exists and must be determined by carefully weighing the degradation costs against the operational flexibility and costs for each potential unit type.
In conclusion, moving from a single, fully-utilized battery energy storage system to a managed multi-battery energy storage system with SOC-based operational constraints is a powerful strategy. It not only extends the practical lifespan of the storage assets but also enhances the overall economic viability of renewable-integrated hybrid power systems. Future work could integrate this operational optimization with the simultaneous design (sizing) of such a multi-battery energy storage system and consider more detailed degradation physics. The proposed model provides a essential tool for unlocking the full economic potential of battery energy storage systems in a sustainable energy landscape.
