As the global energy landscape shifts towards sustainability, the integration of renewable sources like solar power has become paramount. Off-grid solar systems offer a promising solution for decentralized energy generation, particularly in remote areas. This paper focuses on optimizing the configuration of large-scale off-grid solar systems for hydrogen production, which combines photovoltaic energy conversion with electrolysis to store and utilize clean energy. The system includes photovoltaic arrays, electrolyzers, hydrogen storage tanks, and fuel cells, forming a self-sufficient energy ecosystem. By leveraging mathematical modeling and optimization algorithms, we aim to minimize total costs while ensuring reliable operation. The study emphasizes the economic and technical feasibility of such systems, highlighting their role in reducing carbon emissions and enhancing energy security.
The core of this research lies in developing a comprehensive model for an off-grid solar system that produces hydrogen. This system operates independently of the grid, making it ideal for regions with abundant solar resources but limited infrastructure. The off-grid solar system captures solar energy, converts it to electricity, and uses it to electrolyze water into hydrogen. The hydrogen is then stored or directly used to power fuel cells for electricity generation when solar input is insufficient. This approach not only maximizes renewable energy utilization but also provides a scalable storage solution. In the following sections, we detail the system components, mathematical formulations, optimization strategies, and a case study to validate the approach.
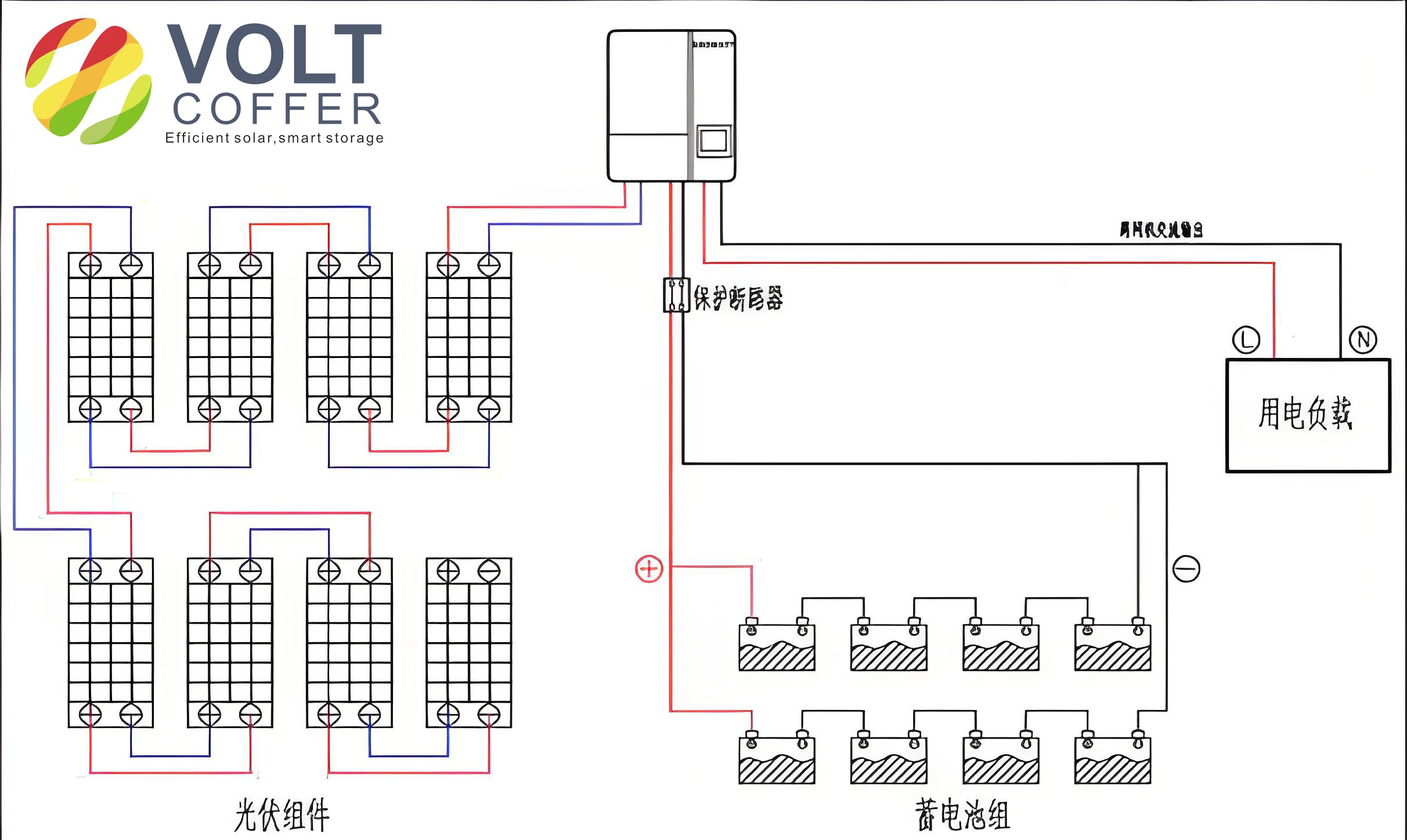
The off-grid solar system comprises several key elements: photovoltaic (PV) arrays, inverters, power conversion equipment, electrolyzers, hydrogen storage tanks, and fuel cells. Each component plays a critical role in ensuring efficient energy flow and storage. The PV arrays convert sunlight into direct current (DC) electricity, which is then inverted to alternating current (AC) for distribution. A portion of this electricity powers local loads, such as residential or industrial users, while the remainder drives the electrolysis process to produce hydrogen. The hydrogen is stored in tanks and can be reconverted to electricity via fuel cells during periods of low solar irradiation. This integrated design allows the off-grid solar system to maintain a continuous energy supply, balancing production and demand dynamically.
To model the off-grid solar system, we define mathematical relationships for each component’s power output. The PV array’s output power at time t, denoted as \( P_{PV}(t) \), is given by:
$$ P_{PV}(t) = \eta_{PV} \cdot \eta_{PVI} \cdot A \cdot G(t) $$
where \( \eta_{PV} \) is the PV conversion efficiency, \( \eta_{PVI} \) is the inverter efficiency, A is the effective area of the PV panels, and \( G(t) \) is the solar irradiance at time t. This equation highlights the dependency of the off-grid solar system on environmental conditions. The power then passes through conversion and distribution equipment, with efficiencies \( \eta_{PCE} \) and \( \eta_{PDE} \), respectively:
$$ P_{PCE}(t) = \eta_{PCE} \cdot P_{PV}(t) $$
$$ P_{PDE}(t) = \eta_{PDE} \cdot P_{PCE}(t) $$
For hydrogen production, the electrolyzer consumes power \( P_{EP}(t) \) to produce hydrogen volume \( V_{EP}(t) \):
$$ P_{EP}(t) = \eta_{HPR} \cdot \eta_{EP} \cdot P_{PDE}(t) $$
$$ V_{EP}(t) = \frac{P_{EP}(t)}{K_{EP,N}} \cdot \Delta t $$
Here, \( \eta_{EP} \) is the electrolyzer efficiency, \( \eta_{HPR} \) is the rectifier efficiency, and \( K_{EP,N} \) is the nominal energy consumption per unit hydrogen. The fuel cell, which converts hydrogen back to electricity, has an output power \( P_{FC}(t) \):
$$ P_{FC}(t) = n_{FC} \cdot V_{FC}(t) \cdot \eta_{FC} \cdot \rho_{H_2} \cdot Q_{H_2}^{DW} $$
where \( n_{FC} \) is the number of fuel cells, \( V_{FC}(t) \) is the hydrogen volume used, \( \eta_{FC} \) is the fuel cell efficiency, \( \rho_{H_2} \) is hydrogen density, and \( Q_{H_2}^{DW} \) is the lower heating value. Hydrogen storage involves charging and discharging powers \( P_{HST,in}(t) \) and \( P_{HST,out}(t) \):
$$ P_{HST,in}(t) = m_{in}(t) \cdot R \cdot V_{in}(t) \cdot \frac{\Delta t_{in}}{\Delta V_{in}} $$
$$ P_{HST,out}(t) = m_{out}(t) \cdot R \cdot V_{out}(t) \cdot \frac{\Delta t_{out}}{\Delta V_{out}} $$
where R is the gas constant, and m and V represent mass and volume changes. These equations form the basis for simulating the off-grid solar system’s behavior under varying conditions.
The optimization of the off-grid solar system aims to minimize the total cost (TC), which includes construction and operating costs. The objective function is:
$$ TC = \min (TCC + TOC) $$
where TCC is the total construction cost and TOC is the total operating cost. TCC is expressed as:
$$ TCC = P_{PV} C_{PV} + P_{PVI} C_{PVI} + P_{PCE} C_{PCE} + P_{PDE} C_{PDE} + P_{EP} C_{EP} + P_{FC} C_{FC} + P_{HST} C_{HST} $$
Here, each P represents the rated power of the component, and C denotes the unit cost. For example, \( C_{PV} \) is the cost per kW for PV panels. TOC is time-dependent and given by:
$$ TOC = P_{PV}(t) C_{PV,O} + P_{PVI}(t) C_{PVI,O} + P_{PCE}(t) C_{PCE,O} + P_{PDE}(t) C_{PDE,O} + P_{EP}(t) C_{EP,O} + P_{FC}(t) C_{FC,O} + P_{HST}(t) C_{HST,O} $$
where the O subscript indicates operating costs per unit power per day. This cost structure ensures that the off-grid solar system is evaluated over its lifecycle.
Constraints are essential to ensure the off-grid solar system operates within safe and practical limits. The power balance constraint is:
$$ P_{PV}(t) + P_{HST,out}(t) = P_{FC}(t) + P_{HST,in}(t) $$
$$ P_{EP} \leq P_{PDE} \leq P_{PCE} \leq P_{PV} $$
This ensures that energy generation and consumption are balanced. Component-specific constraints include:
$$ P_{PV}(t) \leq P_{PV,N} $$
$$ P_{PVI}(t) \leq P_{PVI,N} $$
$$ P_{PCE}(t) \leq P_{PCE,N} $$
$$ P_{PDE}(t) \leq P_{PDE,N} $$
$$ P_{EP,min} \leq P_{EP}(t) \leq P_{EP,max} $$
$$ P_{FC}(t) \leq P_{FC,max} $$
$$ P_{EP,min} \leq P_{HST,out}(t) \leq P_{HST,in}(t) \leq P_{EP,max} $$
These constraints protect the equipment from overloading and ensure efficient operation of the off-grid solar system.
To solve this optimization problem, we employ the Particle Swarm Optimization (PSO) algorithm. PSO is a population-based method inspired by social behavior, such as bird flocking. It iteratively adjusts particles’ positions (solutions) in the search space to find the optimum. For the off-grid solar system, each particle represents a potential configuration of component sizes. The algorithm updates velocities and positions based on individual and global best solutions, minimizing the total cost. The steps include initialization, evaluation, and iteration until convergence. PSO is chosen for its simplicity, robustness, and ability to handle nonlinear constraints, making it suitable for optimizing the complex off-grid solar system.
In our case study, we consider a hypothetical region with high solar irradiation, similar to arid areas. The off-grid solar system is designed with a 200 MW PV capacity. Solar irradiance data, residential load profiles, and hydrogen demand are synthesized based on typical patterns. For instance, solar irradiance peaks at midday, while hydrogen demand might be steady for industrial use. The component parameters are summarized in the following tables:
| Parameter | Value |
|---|---|
| Maximum Power (kW) | 0.545 |
| Area (m²) | 2.58 |
| Efficiency (%) | 21.3 |
| Unit Cost ($/kW) | 1800 |
| Operating Cost ($/kW/day) | 0.12 |
| Parameter | Value |
|---|---|
| Rated Power (kW) | 320 |
| Efficiency (%) | 99.01 |
| Unit Cost ($/kW) | 200 |
| Operating Cost ($/kW/day) | 0.08 |
| Parameter | Value |
|---|---|
| Rated Power (kW) | 200,000 |
| Voltage (kV) | 35 |
| Conversion Efficiency (%) | 90 |
| Unit Cost ($/kW) | 300 |
| Operating Cost ($/kW/day) | 0.02 |
| Parameter | Value |
|---|---|
| Rated Power (kW) | 5,000 |
| Hydrogen Production Rate (Nm³/h) | 1,000 |
| Energy Consumption (kWh/Nm³) | 5 |
| Efficiency (%) | 70 |
| Unit Cost ($/kW) | 2,000 |
| Operating Cost ($/kW/day) | 0.22 |
| Parameter | Value |
|---|---|
| Peak Power (kW) | 200 |
| Efficiency (%) | 53 |
| Power Density (kW/L) | 4.9 |
| Hydrogen Density (kg/m³) | 0.0899 |
| Lower Heating Value (MJ/kg) | 120.5 |
| Unit Cost ($/kW) | 3,000 |
| Operating Cost ($/kW/day) | 0.01 |
| Parameter | Value |
|---|---|
| Volume (m³) | 2,000 |
| Pressure (MPa) | 2 |
| Gas Constant (J/K/mol) | 8.314 |
| Unit Cost ($/kW) | 785.36 |
| Operating Cost ($/kW/day) | 0.07 |
Using PSO with a population size of 200 and maximum iterations of 600, we optimize the off-grid solar system configuration. The inertia weight is set to 0.5, and acceleration constants are 1.4954. The algorithm converges after 249 iterations, yielding a minimum total cost of approximately $128 million. The fitness curve shows a steady decline, indicating effective optimization. This result demonstrates the economic viability of the off-grid solar system for hydrogen production.
The optimized operation profiles for the fuel cell and hydrogen storage tank over a typical 24-hour period are analyzed. The fuel cell power output varies based on hydrogen availability and electricity demand, peaking during evening hours when solar input is low. The storage tank charging and discharging powers balance the system, with charging occurring during high solar generation and discharging during demand peaks. These profiles ensure that the off-grid solar system maintains reliability without grid support.
In conclusion, this study presents a robust framework for optimizing large-scale off-grid solar systems integrated with hydrogen production. The mathematical model and PSO algorithm effectively minimize costs while adhering to operational constraints. The off-grid solar system demonstrates significant potential for renewable energy utilization, energy storage, and decarbonization. Future work could explore real-time control strategies and integration with other renewables to enhance the off-grid solar system’s performance. Overall, the off-grid solar system represents a sustainable solution for remote and off-grid applications, contributing to global energy transition goals.
