As the global shift towards renewable energy intensifies, wind power has emerged as a pivotal component in modern power grids. However, the inherent intermittency and volatility of wind generation pose significant challenges to grid stability and dispatchability. In addressing these issues, the integration of a battery energy storage system (BESS) with wind farms has proven to be an effective solution. This article presents a comprehensive multi-objective optimization control strategy for a battery energy storage system designed to enhance wind power integration by simultaneously tracking generation schedules and mitigating power fluctuations. The approach leverages advanced algorithms and evaluation frameworks to optimize the performance of the battery energy storage system, ensuring grid compliance and extending battery lifespan.
The core of this work revolves around a “three-station-in-one” wind-storage combined system, where a wind farm and a battery energy storage system are coupled through a specialized substation. The topology facilitates seamless power exchange and quality control. Specifically, the battery energy storage system compensates for deviations between actual wind power and scheduled generation, while also smoothing out short-term power swings. This dual functionality is critical for meeting grid codes and improving the economic viability of wind energy. The following sections detail the system modeling, objective formulation, optimization techniques, and validation results, all from the perspective of my research and implementation.
To begin, the power dynamics of the combined system are defined. Let \( P_{wind}(t) \) denote the actual power output from the wind turbines at time \( t \), \( P_{bess}(t) \) the power output from the battery energy storage system (positive for discharge, negative for charge), and \( P_{out}(t) \) the total power injected into the grid. The fundamental relationship is:
$$ P_{out}(t) = P_{wind}(t) + P_{bess}(t) $$
The battery energy storage system’s power is decomposed into two components: one for tracking the generation plan \( P_{plan}(t) \) and another for smoothing wind power fluctuations. Formally:
$$ P_{bess}(t) = P_{bess-1}(t) + P_{bess-2}(t) $$
where \( P_{bess-1}(t) \) addresses schedule tracking, and \( P_{bess-2}(t) handles fluctuation mitigation. The state of charge (SOC) of the battery energy storage system evolves according to:
$$ SOC(t + \Delta t) = (1 – \rho) SOC(t) – \frac{\int_{t}^{t+\Delta t} P_{batt}(\tau) d\tau}{C_{rate}} $$
Here, \( \rho \) is the self-discharge rate, \( C_{rate} \) is the rated capacity, and \( P_{batt}(t) \) represents the actual battery power, accounting for charging and discharging efficiencies \( \eta_{char} \) and \( \eta_{dis} \):
$$ P_{batt}(t) = F_{char} \eta_{char} P_{bess}(t) + F_{dis} \frac{P_{bess}(t)}{\eta_{dis}} $$
with \( F_{char} \) and \( F_{dis} \) being binary flags indicating charge or discharge modes. The constraints on the battery energy storage system include power limits and SOC boundaries to prevent overcharge or deep discharge.
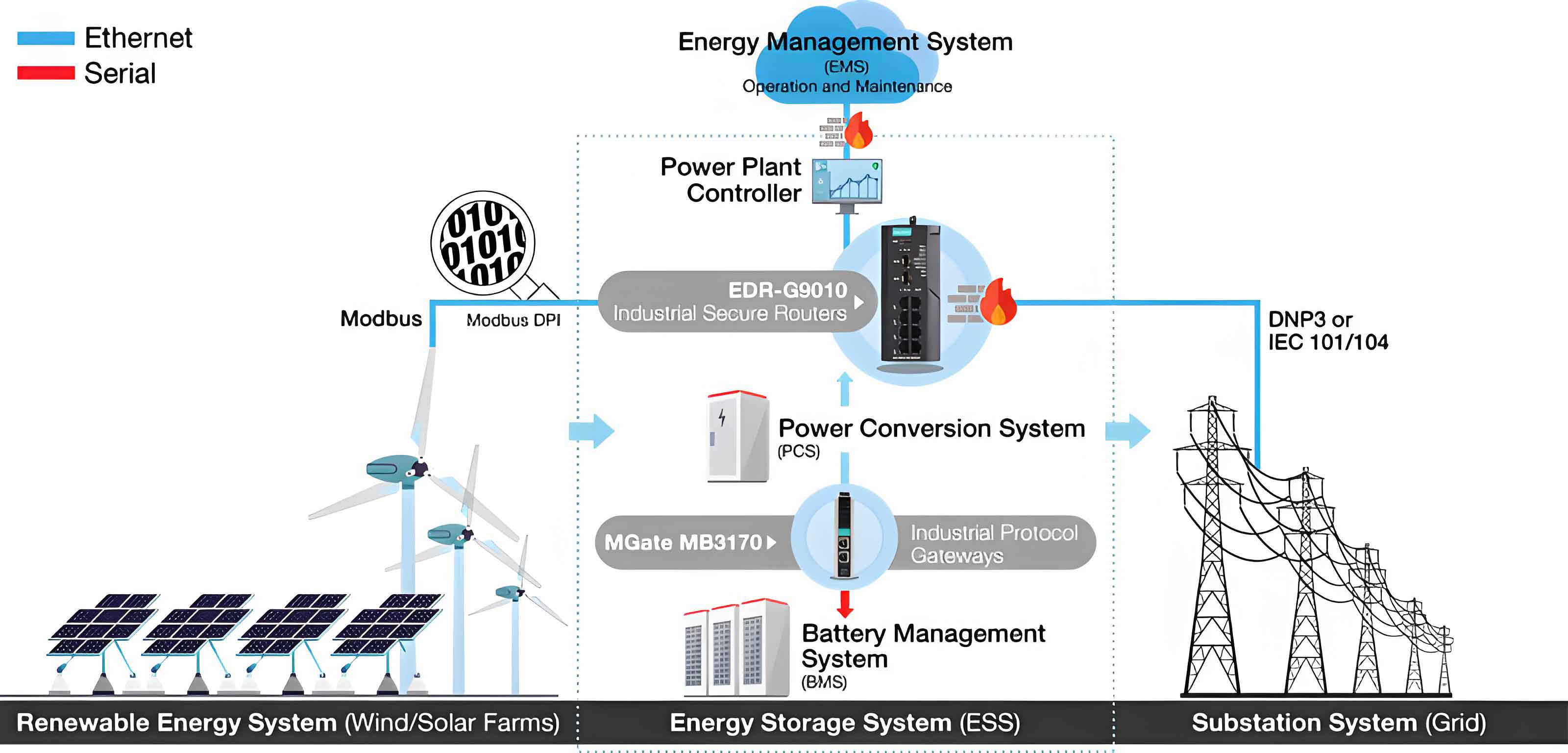
To assess the performance of the battery energy storage system in this application, a set of evaluation metrics is established. These metrics align with grid standards and operational goals. First, the accuracy of tracking the generation schedule is quantified. Define the instantaneous tracking accuracy \( \gamma_{plan}(t) \) as:
$$ \gamma_{plan}(t) = 1 – \frac{| P_{out}(t) – P_{plan}(t) |}{P_c(t)} $$
where \( P_c(t) \) is the available wind capacity. The overall tracking accuracy over a period \( N \) steps is:
$$ \phi_{plan} = 1 – \sqrt{\frac{1}{N} \sum_{t=1}^{N} \left(1 – \gamma_{plan}(t)\right)^2} $$
The compliance rate with the schedule, considering a tolerance \( \varepsilon_1 \), is:
$$ B_{plan} = \frac{1}{N} \sum_{t=1}^{N} F_{plan}(\gamma_{plan}(t)), \quad \text{where } F_{plan}(x) = \begin{cases} 1, & x \geq 1 – \varepsilon_1 \\ 0, & x < 1 – \varepsilon_1 \end{cases} $$
Second, for power fluctuation mitigation, the rate of change over a time window \( T_{flu} \) (e.g., 10 minutes) is evaluated. The fluctuation rate \( \gamma_{flu}(t) \) is:
$$ \gamma_{flu}(t) = \frac{\max_{k \in [t-T_{flu}, t]} P_{out}(k) – \min_{k \in [t-T_{flu}, t]} P_{out}(k)}{S_c} $$
with \( S_c \) being the installed wind capacity. The smoothness index and compliance rate are:
$$ \phi_{flu} = \frac{1}{N} \sum_{t=1}^{N} \gamma_{flu}(t), \quad B_{flu} = \frac{1}{N} \sum_{t=1}^{N} F(\varepsilon_2 – \gamma_{flu}(t)) $$
where \( \varepsilon_2 \) is the fluctuation limit, and \( F(x) = 1 \) if \( x \geq 0 \), else 0. Third, to account for battery longevity, the cumulative charge and discharge energies are tracked:
$$ E_{char} = \sum_{t=1}^{N} | P_{batt}(t) \cdot F(-P_{batt}(t)) | \cdot T, \quad E_{dis} = \sum_{t=1}^{N} | P_{batt}(t) \cdot F(P_{batt}(t)) | \cdot T $$
$$ E_{sum} = E_{char} + E_{dis} $$
where \( T \) is the control time step. These metrics collectively form the basis for optimizing the battery energy storage system’s operation.
The optimization problem is formulated as a multi-objective model, aiming to minimize four conflicting objectives. The first objective \( f_1 \) penalizes deviations from the generation schedule beyond the tolerance \( \varepsilon_1 \):
$$ f_1(t) = \begin{cases} 0, & 1 – \gamma_{plan}(t) \leq \varepsilon_1 \\ a_1 \left(1 – e^{\frac{(\varepsilon_1 – (1 – \gamma_{plan}(t)))^2}{b_1^2}}\right) + 1 – a_1, & \text{otherwise} \end{cases} $$
The second objective \( f_2 \) addresses excessive power fluctuations:
$$ f_2(t) = \begin{cases} 0, & \gamma_{flu}(t) \leq \varepsilon_2 \\ a_2 \left(1 – e^{\frac{(\varepsilon_2 – \gamma_{flu}(t))^2}{b_2^2}}\right), & \text{otherwise} \end{cases} $$
The third objective \( f_3 \) focuses on reducing the depth of discharge in each control interval to prolong battery life:
$$ f_3(t) = \frac{\int_{t}^{t+T} | P_{batt}(\tau) | d\tau}{C_{rate}} $$
The fourth objective \( f_4 \) manages the SOC of the battery energy storage system, encouraging operation within a healthy range. The SOC is partitioned into zones: over-discharge zone \( Z_1 \), discharge warning zone \( Z_2 \), charge倾向 zone \( Z_3 \), discharge倾向 zone \( Z_4 \), charge warning zone \( Z_5 \), and over-charge zone \( Z_6 \). The function \( f_4 \) varies for charging and discharging:
For charging (\( P_{bess} \leq 0 \)):
$$ f_{4,char}(SOC) = \begin{cases} 1, & SOC < SOC_{min} \\ \frac{SOC – SOC_a}{SOC_{min} – SOC_a}, & SOC_{min} \leq SOC < SOC_a \\ 0, & SOC_a \leq SOC \leq SOC_b \\ 1 – \sqrt{1 – \left(\frac{SOC – SOC_b}{SOC_{max} – SOC_b}\right)^2}, & SOC_b < SOC \leq SOC_{max} \\ 1, & SOC > SOC_{max} \end{cases} $$
For discharging (\( P_{bess} > 0 \)):
$$ f_{4,dis}(SOC) = \begin{cases} 1, & SOC < SOC_{min} \\ 1 – \sqrt{1 – \left(\frac{SOC – SOC_b}{SOC_{min} – SOC_b}\right)^2}, & SOC_{min} \leq SOC < SOC_b \\ 0, & SOC_b \leq SOC \leq SOC_c \\ \frac{SOC – SOC_c}{SOC_{max} – SOC_c}, & SOC_c < SOC \leq SOC_{max} \\ 1, & SOC > SOC_{max} \end{cases} $$
Thus, \( f_4(t) = f_{4,char} \) or \( f_{4,dis} \) based on the power direction. The overall multi-objective optimization model is:
$$ \min \mathbf{F} = [f_1, f_2, f_3, f_4] $$
subject to the power balance, SOC dynamics, and operational constraints of the battery energy storage system. The constraints include:
$$ P_{batt}(t) \leq \min \left\{ P_{dis}^{max}, \frac{[(1-\rho)SOC(t) – SOC_{min}] C_{rate}}{T} \right\} $$
$$ -P_{batt}(t) \leq \min \left\{ P_{char}^{max}, \frac{[SOC_{max} – (1-\rho)SOC(t)] C_{rate}}{T} \right\} $$
where \( P_{dis}^{max} \) and \( P_{char}^{max} \) are the maximum discharge and charge powers of the battery energy storage system.
To solve this multi-objective problem, I employ the NSGA-II (Non-dominated Sorting Genetic Algorithm II), which is well-suited for handling non-convex and discontinuous Pareto fronts. The algorithm works by maintaining a population of candidate solutions, ranking them based on non-domination, and using crowding distance to preserve diversity. The steps are: initialization, non-dominated sorting, crowding distance calculation, selection, crossover, and mutation. After convergence, a set of Pareto-optimal solutions is obtained. However, since the control requires a single decision at each time step, a fuzzy comprehensive evaluation method is applied to select the best compromise solution from the Pareto set.
The fuzzy evaluation involves defining an indicator set \( I = \{f_1, f_2, f_3, f_4\} \) and a judgment set \( V = \{\text{NB, NS, ZO, PS, PB}\} \) representing negative big, negative small, zero, positive small, and positive big. Weights \( w = [w_1, w_2, w_3, w_4] \) are assigned using the Analytic Hierarchy Process (AHP) to reflect the relative importance of each objective. For each solution in the Pareto set, the membership degrees to the judgment grades are computed via predefined membership functions. The comprehensive membership vector \( \mathbf{B} = [b_1, b_2, b_3, b_4, b_5] \) is derived using a weighted average operator:
$$ b_j = \min \left(1, \sum_{i=1}^{4} w_i r_{ij}\right) $$
where \( r_{ij} \) is the membership of objective \( i \) to grade \( j \). A score vector \( \mathbf{S} = [30, 55, 75, 90, 100] \) is then used to calculate a total score \( G \):
$$ G = \sum_{j=1}^{5} b_j s_j $$
The solution with the highest \( G \) is chosen as the optimal power command for the battery energy storage system at that time step. This hybrid approach ensures real-time, adaptive control that balances all objectives effectively.
For validation, I conducted a case study using real-world data from a 50 MW wind farm coupled with a 10 MW/20 MWh battery energy storage system. The control time step is 5 minutes, and the evaluation period is 24 hours (288 points). The parameters for the objectives and constraints are summarized in the table below.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| \( P_{char}^{max} \) | 10 MW | \( \eta_{char} \) | 0.9 |
| \( P_{dis}^{max} \) | 10 MW | \( \eta_{dis} \) | 0.9 |
| \( SOC_0 \) | 0.5 | \( SOC_{min} \) | 0.2 |
| \( SOC_{max} \) | 0.9 | \( SOC_a \) | 0.4 |
| \( SOC_b \) | 0.55 | \( SOC_c \) | 0.7 |
| \( a_1 \) | 0.2 | \( b_1 \) | 0.13 |
| \( a_2 \) | 1.0 | \( b_2 \) | 0.15 |
| \( \varepsilon_1 \) | 0.1 | \( \varepsilon_2 \) | 0.15 |
| \( \mathbf{w} \) | [0.4681, 0.2811, 0.0677, 0.1831] | \( \mathbf{S} \) | [30, 55, 75, 90, 100] |
Three scenarios are compared: Scenario 1 (no battery energy storage system), Scenario 2 (BESS with fuzzy control for schedule tracking only), and Scenario 3 (the proposed multi-objective strategy). The results are presented in the following table.
| Scenario | \( \phi_{plan} \) (%) | \( B_{plan} \) (%) | \( B_{flu} \) (%) | \( \phi_{flu} \) | \( E_{char} \) (MWh) | \( E_{dis} \) (MWh) |
|---|---|---|---|---|---|---|
| Scenario 1 | 91.38 | 70.83 | 99.31 | 0.044 | — | — |
| Scenario 2 | 93.73 | 96.53 | 100 | 0.028 | 16.092 | 8.022 |
| Scenario 3 | 92.71 | 100 | 100 | 0.033 | 11.978 | 3.812 |
The analysis shows that without a battery energy storage system, the schedule compliance is poor (70.83%). Scenario 2 improves tracking but at the cost of higher battery usage, leading to significant charge and discharge energies. In contrast, the proposed multi-objective strategy (Scenario 3) achieves perfect schedule compliance (100%) while maintaining fluctuation compliance at 100%. Moreover, the battery energy storage system’s energy throughput is substantially reduced: charge energy decreases from 16.092 MWh to 11.978 MWh, and discharge energy from 8.022 MWh to 3.812 MWh. This indicates less stress on the battery energy storage system, which translates to extended cycle life.
Further examination of the SOC trajectory reveals that Scenario 3 keeps the SOC within a narrower band (0.41 to 0.70) compared to Scenario 2 (0.30 to 0.81), reducing the SOC swing by 40%. The number of charge-discharge cycles is also lower in Scenario 3, demonstrating the effectiveness of the multi-objective optimization in preserving the battery health. The power output of the battery energy storage system in Scenario 3 is more modulated, avoiding unnecessary interventions during periods of minor fluctuations or small schedule deviations.
In conclusion, the integration of a battery energy storage system with wind power through a multi-objective optimization framework offers a robust solution for grid integration challenges. The developed strategy simultaneously addresses generation schedule tracking, power fluctuation mitigation, and battery longevity. By employing NSGA-II and fuzzy comprehensive evaluation, the battery energy storage system’s power commands are optimized in real-time, ensuring a balance between grid requirements and operational efficiency. The case study confirms that the proposed approach enhances the dispatchability of wind power, reduces grid instability, and prolongs the service life of the battery energy storage system. Future work could explore the inclusion of forecast uncertainties or the extension to hybrid energy storage systems for broader applications.
Throughout this article, the term “battery energy storage system” has been emphasized to underscore its pivotal role. The methodology and results presented here provide a foundation for advancing the deployment of battery energy storage systems in renewable-rich grids, contributing to a more sustainable and resilient energy future.
