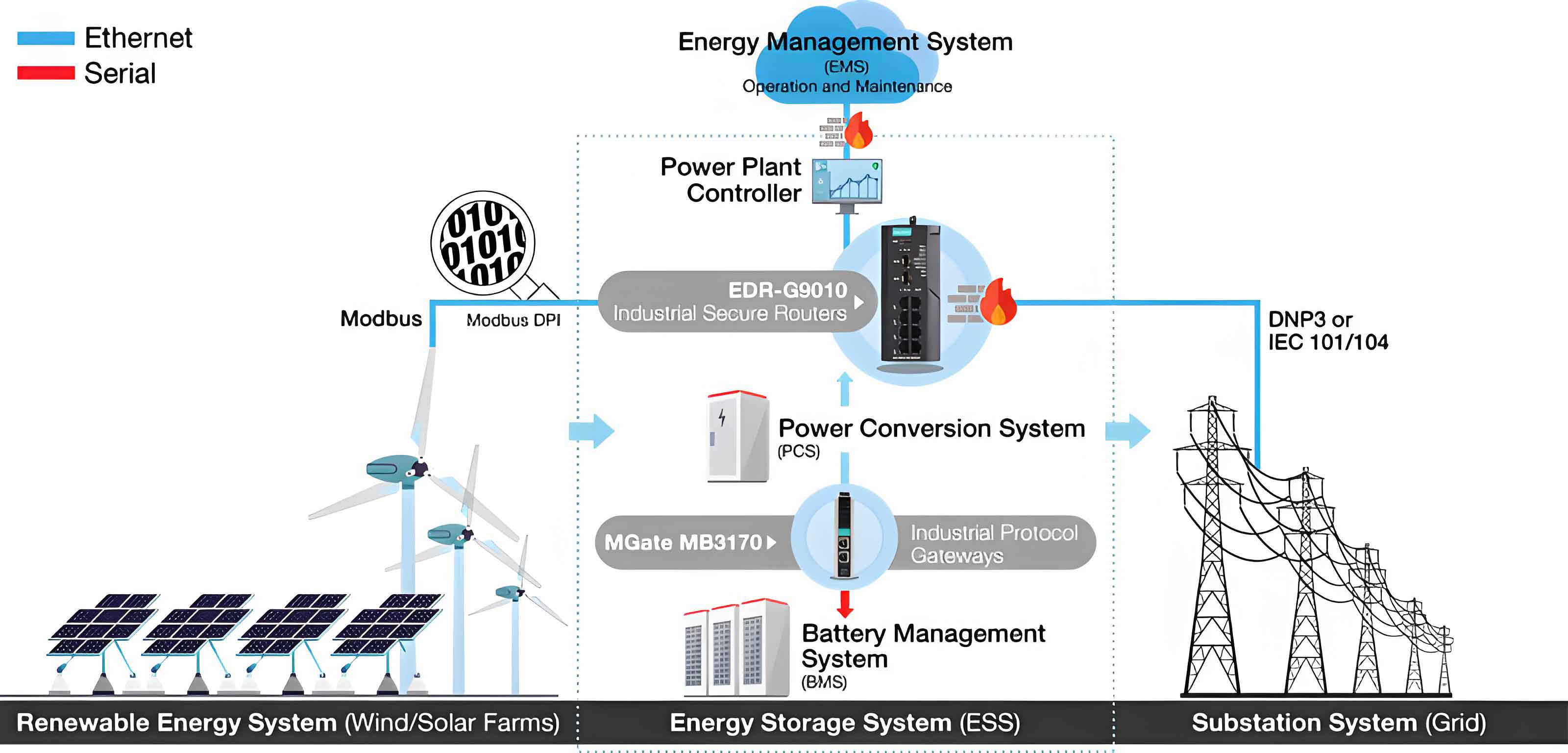
The integration of renewable energy sources like wind and solar into the power grid presents significant challenges due to their inherent intermittency and volatility. To ensure grid stability, reliability, and economic efficiency, energy storage systems have become indispensable. Among them, the Battery Energy Storage System (BESS) plays a pivotal role in providing rapid response for power balancing, frequency regulation, and peak shaving. The core of an effective BESS lies in its power conversion system and, more importantly, the control strategy governing its charge and discharge cycles. A sophisticated control algorithm must not only manage power flow precisely but also protect the battery from harmful operating conditions such as overcharge and deep discharge, thereby extending its lifespan. This article delves into the detailed modeling, control design, and simulation of a grid-connected BESS, focusing on a bidirectional DC/DC converter regulated by a dual-loop Proportional-Integral (PI) control scheme.
The performance and dynamic response of a battery energy storage system are critically dependent on its power electronic interface. The primary function of this interface is to facilitate bidirectional energy transfer between the battery bank, typically at a variable low-voltage DC level, and a common DC bus or directly to an AC grid via an inverter. For this purpose, a non-isolated bidirectional half-bridge DC/DC converter is often favored for its simplicity, high efficiency, and cost-effectiveness, especially in medium to low-power applications. This converter can operate in two fundamental modes: Buck mode (stepping down voltage) for charging the battery from a higher voltage DC bus, and Boost mode (stepping up voltage) for discharging the battery to supply power to the DC bus. The seamless transition between these modes is a key requirement for the battery energy storage system controller.
The heart of the proposed control strategy for the battery energy storage system is a cascaded dual-loop PI controller. This structure offers superior performance compared to single-loop control by providing faster dynamic response and better disturbance rejection. The outer loop is typically a voltage control loop. Its objective is to maintain the DC-link voltage ($V_{dc}$) at a constant reference value ($V_{dc}^{*}$), regardless of load variations or fluctuations in power generation. The voltage error is processed by a PI controller, whose output serves as the reference command for the inner loop.
The inner loop is a current control loop. It dictates the inductor current ($i_L$) of the bidirectional DC/DC converter to follow the reference current ($i_{L}^{*}$) generated by the voltage loop. Controlling the current directly offers several advantages for the battery energy storage system: it provides inherent current limiting to protect the semiconductor switches and the battery, improves the system’s bandwidth for faster response to transients, and simplifies the compensation design. The PI controller for the current loop is tuned to achieve a swift and accurate tracking response. The output of this inner-loop PI controller is compared with a carrier wave to generate the Pulse-Width Modulation (PWM) signals for the converter’s switches, thereby controlling the power flow direction and magnitude.
The mathematical representation of a PI controller in the Laplace domain is given by:
$$ W_{PI}(s) = K_p + \frac{K_i}{s} $$
where $K_p$ is the proportional gain, $K_i$ is the integral gain, and $s$ is the complex frequency variable. The transfer functions for the voltage and current plant models need to be derived from the state-space averaging model of the bidirectional converter in both operating modes to facilitate proper controller design.
For a systematic design of the battery energy storage system controller, a state-space averaged model of the bidirectional half-bridge converter is essential. Considering the converter operating in Boost mode (discharge), the state variables are typically the inductor current ($i_L$) and the output capacitor voltage ($v_{C}$). The averaged state-space equations over a switching period can be derived as:
$$ L \frac{d\langle i_L \rangle}{dt} = V_{bat} – (1-d) \langle v_C \rangle $$
$$ C \frac{d\langle v_C \rangle}{dt} = (1-d)\langle i_L \rangle – \frac{\langle v_C \rangle}{R_{load}} $$
where $L$ is the filter inductance, $C$ is the DC-link capacitance, $V_{bat}$ is the battery voltage, $d$ is the duty cycle of the lower switch (for Boost mode), $R_{load}$ is the load resistance, and $\langle \cdot \rangle$ denotes averaged quantities. A similar set of equations can be formulated for Buck mode operation. Linearizing these equations around a steady-state operating point allows for the derivation of small-signal transfer functions, such as the control-to-inductor-current transfer function $G_{id}(s)$ and the control-to-output-voltage transfer function $G_{vd}(s)$. These transfer functions are crucial for applying frequency-domain techniques to tune the PI controllers in the dual-loop structure for the battery energy storage system.
To validate the proposed control strategy, a comprehensive simulation model of the battery energy storage system was developed in MATLAB/Simulink. The model comprises several key subsystems, as summarized in the table below:
| Subsystem/Component | Description & Key Parameters |
|---|---|
| Battery Model | Implemented using Simscape Electrical ‘Battery’ block. Model type: Lithium-Ion. Parameters: Nominal Voltage = 200V, Rated Capacity = 9.6Ah, Initial State-of-Charge (SOC) = 90%. A battery management logic enforces SOC limits (e.g., 20% to 100%) to prevent damage. |
| Bidirectional DC/DC Converter | Half-bridge topology with IGBTs and anti-parallel diodes. Components: Filter inductor L = 2mH, DC-link capacitor C = 2200µF, Switching Frequency = 10 kHz. |
| Dual-Loop PI Controller | Implemented using discrete PI blocks. Voltage Loop: $K_{p,v}$ = 0.55, $K_{i,v}$ = 13. Current Loop: $K_{p,i}$ = 1.2, $K_{i,i}$ = 25. Includes mode selection logic based on power flow direction. |
| Load & Source Model | A controlled voltage source in series with a resistor simulates a variable load (when source voltage < DC-link voltage) or a charging source (when source voltage > DC-link voltage). |
The control objectives for the simulated battery energy storage system were defined as follows:
1. Maintain the DC-link voltage at a constant reference of 400 V.
2. Ensure smooth and rapid transition between charging and discharging modes based on source/load conditions.
3. Regulate the battery charge/discharge current to prevent excessive stress.
4. Enforce SOC boundaries for battery protection.
The system was subjected to a dynamic test sequence to evaluate the controller’s performance:
– Phase 1 (0 – 0.4 s): Discharge mode. The simulated load is active, drawing power from the battery energy storage system via the DC bus.
– Phase 2 (0.4 – 1.2 s): Increased Load Discharge. The load resistance is decreased at t=0.4s, demanding more power.
– Phase 3 (1.2 – 2.0 s): Charge mode. The external source voltage is set higher than the DC-link reference, forcing power to flow into the battery energy storage system.
The simulation results demonstrated the effectiveness of the dual-loop PI control strategy. The following table summarizes the key observed behaviors:
| Performance Metric | Simulation Result & Analysis |
|---|---|
| DC-Link Voltage Regulation | The voltage ($V_{dc}$) remained tightly regulated at 400V ± 2%. During the load step change at t=0.4s, a minimal transient deviation of less than 15V was observed, which was corrected by the voltage loop within 50ms. |
| Battery Current Response | The inductor current ($i_L$) tracked its reference swiftly. Positive current indicated discharge, negative indicated charge. The transition at t=1.2s was seamless, with no significant current overshoot, showcasing the inner current loop’s fast dynamics. |
| Battery State-of-Charge (SOC) | The SOC decreased linearly during Phase 1 and 2, confirming discharge. During Phase 3, the SOC increased, confirming charge. The trend validated correct power flow management in the battery energy storage system. |
| Mode Transition | The controller logic successfully identified the required power flow direction and activated the appropriate converter switches (Buck or Boost mode) without instability. |
The dynamic response can be further analyzed by considering the system’s closed-loop bandwidth. For the inner current loop, a high bandwidth is desirable. The designed PI controller yielded a loop gain crossover frequency ($f_{c,i}$) approximately at one-tenth of the switching frequency, which is a common rule of thumb for stability:
$$ f_{c,i} \approx \frac{f_{sw}}{10} = 1 \text{kHz} $$
The voltage loop, being the slower outer loop, was designed with a bandwidth ($f_{c,v}$) roughly one decade lower than the current loop bandwidth to ensure proper loop separation and stability:
$$ f_{c,v} \approx \frac{f_{c,i}}{10} = 100 \text{Hz} $$
This hierarchical bandwidth allocation is a fundamental principle in cascaded control design for power converters, including those in a battery energy storage system.
In conclusion, the modeling and simulation study confirms the viability and effectiveness of a dual-loop PI control strategy for managing the charge and discharge cycles of a battery energy storage system. The use of a bidirectional half-bridge DC/DC converter as the power interface, governed by cascaded voltage and current control loops, provides excellent DC-link voltage regulation, fast dynamic response to load and source changes, and smooth transitions between operating modes. The simulation model, built with detailed component representations, serves as a valuable platform for analyzing the behavior of the battery energy storage system under various scenarios. Future work could focus on enhancing this basic control scheme by integrating more advanced strategies such as model predictive control (MPC) for further optimized dynamics, or adaptive control to compensate for battery parameter variations over its lifetime. Furthermore, integrating this unit-level model into a larger system-level simulation involving multiple renewable sources and storage units would be a critical step for studying the holistic grid-support functions of a large-scale battery energy storage system.
