Introduction
Maximum Power Point Tracking (MPPT) is a critical technology in photovoltaic (PV) systems to ensure optimal energy extraction under varying environmental conditions. Traditional MPPT algorithms, such as Perturb and Observe (P&O) and Incremental Conductance (INC), face challenges in complex scenarios like partial shading, where multiple local maxima emerge on the power-voltage (P-U) curve. This study proposes a hybrid optimization algorithm combining an enhanced Cuckoo Search (CS) algorithm with a variable-step P&O method to improve tracking speed, stability, and accuracy under partial shading.
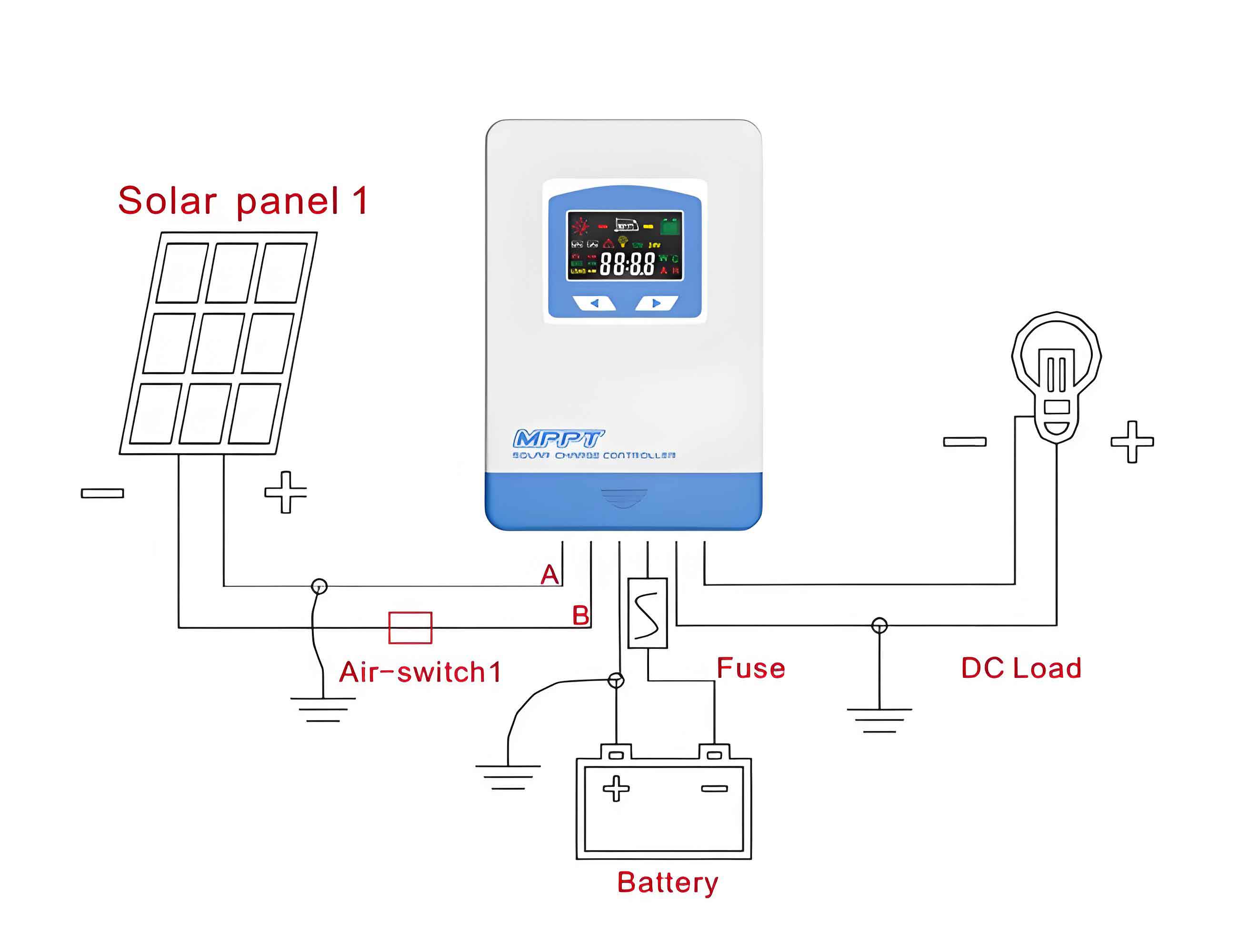
Methodology
1. Enhanced Cuckoo Search Algorithm
The standard Cuckoo Search algorithm mimics the brood parasitism behavior of cuckoos. To address its limitations in convergence speed and oscillation, the following improvements are introduced:
a. Initial Population Optimization
A diversified initialization strategy ensures uniform distribution of candidate solutions across the search space, avoiding premature convergence.
b. Adaptive Step Size Mechanism
The step size αα dynamically adjusts based on the proximity to the global maximum:α=αmax⋅exp(−∣Pcurrent−Pbest∣Pbest)α=αmax⋅exp(−Pbest∣Pcurrent−Pbest∣)
where PcurrentPcurrent is the current power, and PbestPbest is the historical maximum.
c. Position Update Equation
The nest position is updated using:x(t+1)i=x(t)i+α⋅Θ(ϵ−Pa)⋅L(γ)x(t+1)i=x(t)i+α⋅Θ(ϵ−Pa)⋅L(γ)
where:
- L(γ)=r1∣r2∣1/p⋅(x(t)i−x(t)best)L(γ)=∣r2∣1/pr1⋅(x(t)i−x(t)best)
- Θ(⋅)Θ(⋅) is a Heaviside function activating updates when ϵ>Paϵ>Pa.
- r1=0.2r1=0.2 and r2r2 are random numbers.
2. Variable-Step P&O for Local Refinement
After the CS algorithm locates the vicinity of the global maximum, a variable-step P&O method fine-tunes the solution:ΔV={k1⋅∣dPdV∣if dPdV>0k2⋅∣dPdV∣otherwiseΔV={k1⋅dVdPk2⋅dVdPif dVdP>0otherwise
where k1>k2k1>k2 to balance speed and oscillation.
Experimental Setup
The proposed algorithm is validated in MATLAB/Simulink under two scenarios: uniform illumination and partial shading.
1. PV Array Parameters
| Parameter | Value |
|---|---|
| VocVoc | 36.3 V |
| IscIsc | 29 A |
| PmaxPmax | 7.35 A × 29 V = 213.15 W |
2. Partial Shading Conditions
Five PV modules are subjected to irradiance levels (W/m²):
| Module | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Case 1 | 1000 | 1000 | 1000 | 1000 | 1000 |
| Case 2 | 1000 | 900 | 800 | 700 | 600 |
| Case 3 | 800 | 700 | 600 | 500 | 400 |
Temperature is fixed at 25°C, and simulation time is 2 seconds.
Results and Analysis
1. Uniform Illumination
Both algorithms converge to the maximum power point (MPP), but the enhanced CS exhibits superior performance:
| Metric | Standard CS | Enhanced CS |
|---|---|---|
| Convergence Time (s) | 0.56 | 0.16 |
| Steady-State Power (W) | 8508 | 8505 |
| Oscillation Amplitude | ≤5 W | ≤1 W |
2. Partial Shading
Under non-uniform irradiance (Case 2), the hybrid algorithm outperforms the baseline:
| Metric | Standard CS | Enhanced CS |
|---|---|---|
| Convergence Time (s) | 0.80 | 0.17 |
| Steady-State Power (W) | 3360 | 3360 |
| Oscillation Amplitude | ≤3 W | ≤1 W |
The power-voltage curves demonstrate that the enhanced CS achieves smoother tracking with minimal oscillations.
Key Equations and Tables
1. Photocurrent and Diode Current
The PV model equations are:Iph=Isc0[1+t⋅(T−Tref)⋅SSref]Iph=Isc0[1+t⋅(T−Tref)⋅SrefS]Id=n1T3exp(−m1T)Id=n1T3exp(−Tm1)
where t=6.4×10−4t=6.4×10−4, Sref=1.3×104Sref=1.3×104, and m1=235m1=235.
2. Algorithm Parameters
| Parameter | r1r1 | r2r2 | k1k1 | k2k2 |
|---|---|---|---|---|
| Value | 0.2 | Rand[0,1] | 0.05 | 0.01 |
Conclusion
This study presents a hybrid MPPT algorithm integrating an improved Cuckoo Search with variable-step P&O. The enhanced CS achieves rapid convergence (0.17 s vs. 0.80 s) and reduces power oscillations to ≤1 W under partial shading. Future work will focus on real-time hardware implementation and multi-objective optimization for grid-connected PV systems.
