The integration of distributed energy resources, characterized by their cleanliness, low cost, renewability, and wide distribution, is increasingly reshaping modern power systems. This paradigm shift has catalyzed the development of microgrids—localized grids that can operate either connected to or isolated from the main power network. A critical component within a microgrid is the Battery Energy Storage System (BESS), which provides essential services like load leveling, renewable energy firming, and frequency regulation. A fundamental challenge in operating a BESS composed of multiple battery units is ensuring State-of-Charge (SoC) balance among them. Imbalances can lead to situations where some batteries are overcharged or over-discharged while others are underutilized, drastically reducing the overall system’s lifespan, efficiency, and reliability.
Traditional centralized control methods require extensive communication infrastructure and are vulnerable to single points of failure. Distributed control strategies, particularly consensus-based algorithms, have emerged as a robust alternative. These methods enable battery units to coordinate locally with their neighbors to achieve a global objective, such as SoC balancing, without needing a central controller. However, most consensus algorithms rely on continuous or periodic communication, which can burden communication networks with redundant data and is not always necessary given the relatively slow dynamics of SoC.
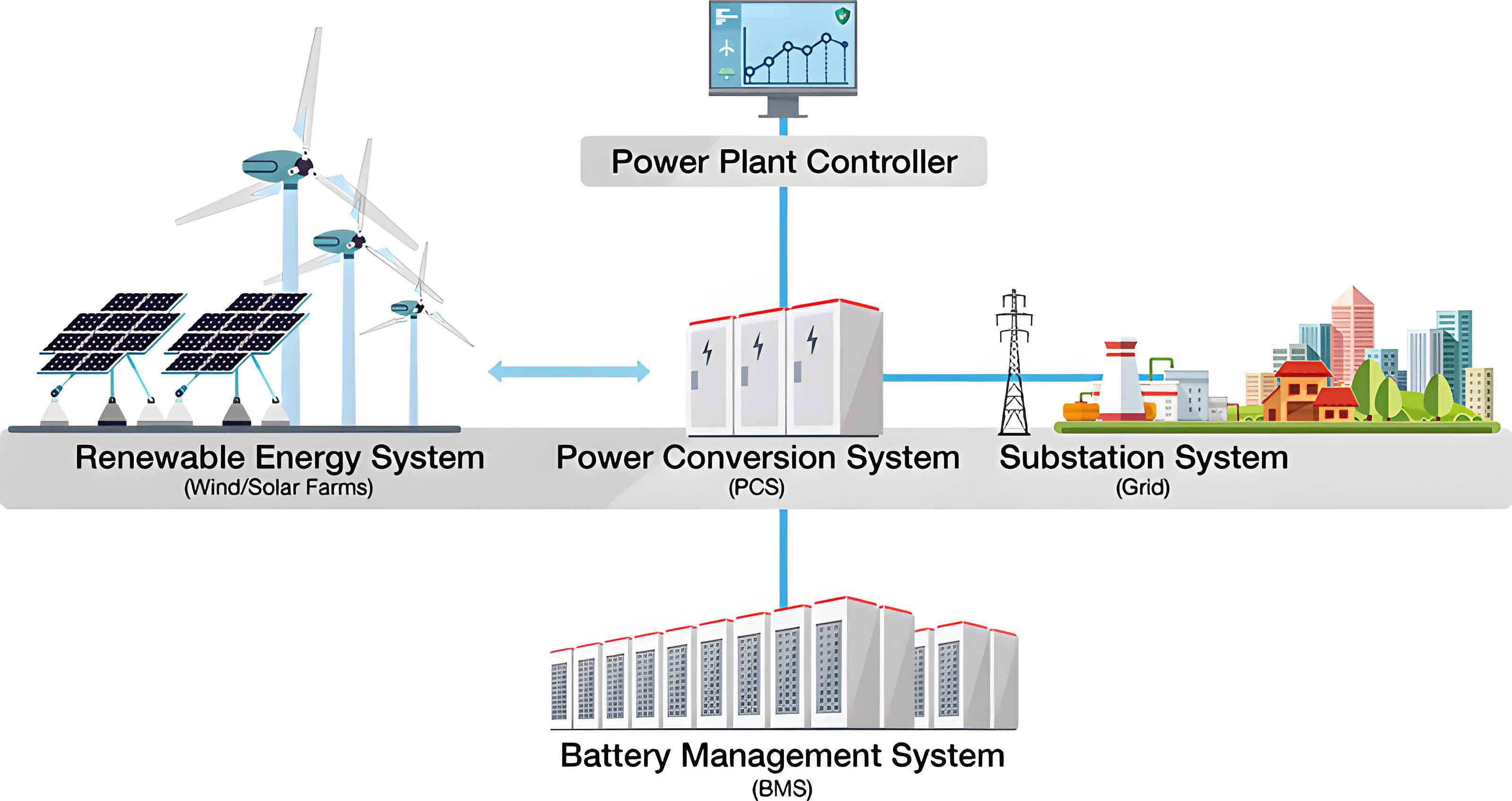
This article addresses the SoC balancing problem for a distributed battery energy storage system within a microgrid. We propose a novel distributed control scheme that integrates an event-triggered communication mechanism with a virtual leader tracking strategy. The primary objectives are threefold: (1) to drive all battery units’ SoC to converge to a common reference value (e.g., 100% for charging or 20% for discharging), thus preventing overcharge/over-discharge; (2) to significantly reduce unnecessary communication among batteries by updating control actions only when necessary, as dictated by a predefined event condition; and (3) to provide a rigorous theoretical framework proving system stability and the absence of Zeno behavior (infinitely fast triggering).
System Modeling and Problem Formulation
Consider a battery energy storage system comprising N battery units. The SoC dynamics for the i-th battery unit can be modeled using the coulomb counting method. Let \(S_i(t)\) denote its SoC, \(C_i\) its nominal capacity, and \(I_i(t)\) its output current (positive for discharge, negative for charge). The dynamic model is:
$$ \dot{S}_i(t) = -\frac{I_i(t)}{C_i}, \quad i=1,2,\ldots,N. $$
Assuming power converter losses are negligible and all units operate at a common DC bus voltage \(V\), the output power \(P_i(t)\) is \(P_i(t) = V I_i(t)\). Substituting this into the SoC dynamic equation yields a direct relationship between power and SoC rate of change:
$$ \dot{S}_i(t) = -\frac{P_i(t)}{C_i V}. $$
For control design, we define the state, input, and a constant parameter as \(x_i(t) = S_i(t)\), \(u_i(t) = P_i(t)\), and \(m_i = -1/(C_i V)\). This transforms the model of each battery unit into a first-order linear system:
$$ \dot{x}_i(t) = m_i u_i(t), \quad i=1,2,\ldots,N. \tag{1} $$
The heterogeneity of the battery energy storage system is captured by the distinct parameters \(m_i\), which depend on each unit’s capacity and voltage.
The communication network among the N battery units is described by a directed graph \(\mathcal{G}=(\mathcal{V},\mathcal{E})\), where \(\mathcal{V}=\{1,2,\ldots,N\}\) is the node set and \(\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}\) is the edge set. An edge \((j, i)\) signifies that unit \(j\) can transmit information to unit \(i\). The adjacency matrix is \(A=[a_{ij}] \in \mathbb{R}^{N \times N}\), and the Laplacian matrix is \(L=[l_{ij}] \in \mathbb{R}^{N \times N}\). To achieve tracking of a desired SoC reference \(x_0(t)\) (the virtual leader), we define a diagonal matrix \(B=\text{diag}(d_1, d_2, \ldots, d_N)\), where \(d_i=1\) if unit \(i\) has direct access to the leader’s state; otherwise, \(d_i=0\).
Assumption 1: The communication graph \(\mathcal{G}\) contains a directed spanning tree, with the virtual leader as the root node. The leader has no incoming edges from followers.
The control objectives for the battery energy storage system are formally stated as follows:
- Charging Mode (\(u_i(t) < 0\)): Drive all battery SoCs to converge to the upper safety threshold (e.g., 100%) asymptotically:
$$ \lim_{t \to \infty} |x_i(t) – x_j(t)| = 0, \quad \lim_{t \to \infty} |x_i(t) – x_0| = 0, \quad \forall i,j, $$
where \(x_0 = 1.0\). The input power \(u_i(t) \to 0\) as SoC reaches the limit. - Discharging Mode (\(u_i(t) > 0\)): Drive all battery SoCs to converge to the lower safety threshold (e.g., 20%) asymptotically:
$$ \lim_{t \to \infty} |x_i(t) – x_j(t)| = 0, \quad \lim_{t \to \infty} |x_i(t) – x_0| = 0, \quad \forall i,j, $$
where \(x_0 = 0.2\). The output power \(u_i(t) \to 0\) as SoC reaches the limit.
Event-Triggered Control Protocol Design
To reduce communication burden, we employ an event-triggered mechanism. Each battery unit \(i\) continuously monitors its own state \(x_i(t)\) but only broadcasts its state to neighbors at certain triggering instants \(t_0^i, t_1^i, t_2^i, \ldots\). Let \(\hat{x}_i(t) = x_i(t_k^i)\) denote the last broadcast state for \(t \in [t_k^i, t_{k+1}^i)\). The state measurement error is defined as \(e_i(t) = \hat{x}_i(t) – x_i(t)\).
We propose the following distributed event-triggered control protocol for the battery energy storage system:
$$ u_i(t) = K \left( \sum_{j \in N_i} a_{ij} (\hat{x}_j(t) – \hat{x}_i(t)) + d_i (x_0 – \hat{x}_i(t)) \right), \tag{2} $$
where \(K > 0\) is a control gain to be designed. This protocol uses only the most recently broadcast states from neighbors and the leader’s reference \(x_0\).
Defining the tracking error for unit \(i\) as \(\delta_i(t) = x_i(t) – x_0\), and stacking vectors \(\delta(t) = [\delta_1(t), \ldots, \delta_N(t)]^T\) and \(e(t) = [e_1(t), \ldots, e_N(t)]^T\), the closed-loop dynamics of the battery energy storage system can be derived from (1) and (2):
$$ \dot{\delta}(t) = -K M (L+B) \delta(t) – K M (L+B) e(t), \tag{3} $$
where \(M = \text{diag}(m_1, m_2, \ldots, m_N)\).
The event-triggering condition for the entire battery energy storage system is chosen as a centralized condition:
$$ t_{k+1} = \inf \{ t > t_k \ | \ \| e(t) \| \geq \sigma \gamma \| \delta(t) \| \}, \tag{4} $$
where \(\sigma \in (0,1)\) is a design parameter, \(\gamma = \lambda_{\min}(L+B) / \|L+B\|\), and \(\lambda_{\min}(L+B)\) is the smallest eigenvalue of matrix \(L+B\). This condition ensures that the measurement error \(e(t)\) remains bounded relative to the collective tracking error \(\delta(t)\). Control updates occur only when this bound is violated, thereby saving communication resources.
Theoretical Analysis and Main Results
We now establish the stability and convergence guarantees for the proposed event-triggered control scheme applied to the battery energy storage system.
Lemma 1: Under Assumption 1, the matrix \(L+B\) is positive definite, and all its eigenvalues have positive real parts.
Lemma 2: Let \(p = [p_1, p_2, \ldots, p_N]^T = (L+B)^{-1} \mathbf{1}\), \(P = \text{diag}(p_1, p_2, \ldots, p_N)\), and \(Q = P(L+B) + (L+B)^T P\). Then matrices \(P\) and \(Q\) are both positive definite.
Using these lemmas, we can state the main convergence theorem.
Theorem 1 (SoC Consensus Convergence): Consider the battery energy storage system (1) under Assumption 1. With the distributed control protocol (2) and the event-triggering condition (4), if the control gain satisfies \(K > 0\), then the system achieves practical leader-following consensus. Specifically, the tracking error \(\delta(t)\) converges to zero asymptotically, implying:
$$ \lim_{t \to \infty} x_i(t) = x_0, \quad \forall i \in \{1,\ldots,N\}. $$
This guarantees that all units in the battery energy storage system will eventually reach the desired target SoC \(x_0\), achieving balanced charging or discharging.
Proof (Sketch): Consider the Lyapunov function candidate \(V(t) = \frac{1}{2} \delta(t)^T P \delta(t)\), where \(P\) is defined in Lemma 2. Calculating its derivative along the trajectories of (3) and using the event condition (4) and properties of \(P\) and \(Q\), one can show that \(\dot{V}(t) \leq -\kappa V(t)\) for some \(\kappa > 0\). This proves exponential stability of \(\delta(t)=0\), confirming the consensus objective for the battery energy storage system. \(\blacksquare\)
A critical issue in event-triggered control is the potential for Zeno behavior, where an infinite number of events occur in a finite time period, making physical implementation impossible. The following theorem proves this is avoided in our battery energy storage system.
Theorem 2 (Exclusion of Zeno Behavior): For the battery energy storage system under the event-triggering rule (4), the inter-event time interval \(\tau_k = t_{k+1} – t_k\) is strictly positive and has a lower bound \(\tau^* > 0\) given by:
$$ \tau^* = \frac{\sigma \gamma}{K \|M\| \|L+B\| (1 + \sigma \gamma)}. $$
This guarantees a minimum time between any two consecutive triggering instants, ensuring the control strategy is physically implementable.
Proof (Sketch): The proof involves analyzing the growth rate of the ratio \(\|e(t)\| / \|\delta(t)\|\) between triggering instants. By deriving a differential inequality for this ratio and integrating from zero until it reaches the threshold \(\sigma \gamma\), a positive lower bound for the inter-event time is obtained. \(\blacksquare\)
Simulation Studies
To validate the proposed event-triggered consensus control for a battery energy storage system, numerical simulations were conducted for both charging and discharging scenarios. The system consists of four heterogeneous battery units. The simulation parameters are summarized in Table 1.
| Parameter | Unit 1 | Unit 2 | Unit 3 | Unit 4 | Unit |
|---|---|---|---|---|---|
| Voltage \(V_i\) | 220 | 220 | 220 | 220 | V |
| Capacity \(C_i\) | 70 | 80 | 75 | 90 | Ah |
| Initial SoC \(x_i(0)\) | 0.75 | 0.85 | 0.72 | 0.85 | p.u. |
| Parameter \(m_i\) | -6.49e-5 | -5.68e-5 | -6.06e-5 | -5.05e-5 | – |
The communication topology follows Figure 1, with Unit 1 and Unit 2 having direct access to the virtual leader (\(d_1=d_2=1\)). The control gain is set to \(K=1.4\), and the event threshold parameter is \(\sigma=0.8\).
Case 1: Charging Mode. The target SoC \(x_0\) is set to 1.0 (100%). The evolution of SoC for all four battery units is shown in Figure 2 (simulated plot). All SoC trajectories converge asymptotically to the target value of 1.0, successfully preventing overcharging. The corresponding input power profiles (negative for charging) for each unit are shown in Figure 3 (simulated plot). The powers converge to zero as the SoC approaches the target, demonstrating proper termination of the charging process. The event-triggering instants are depicted in Figure 4 (simulated plot). The intervals between events are clearly positive and bounded below, confirming the absence of Zeno behavior as proven in Theorem 2.
Case 2: Discharging Mode. The target SoC \(x_0\) is set to 0.2 (20%). The initial SoCs are set to [0.65, 0.73, 0.70, 0.72]. The SoC convergence is shown in Figure 5 (simulated plot), where all states successfully converge to 20%. The output power profiles (positive for discharging) are shown in Figure 6 (simulated plot), decaying to zero as the lower limit is reached, thus preventing over-discharge. The event-triggering sequence for this case is shown in Figure 7 (simulated plot), again validating the existence of a positive minimum inter-event time.
Comparative Analysis and Discussion
The proposed method offers distinct advantages for managing a distributed battery energy storage system. Table 2 provides a concise comparison with other common approaches.
| Feature / Method | Centralized Control | Continuous-Time Consensus | Average-Based Estimation | Proposed Event-Triggered + Virtual Leader |
|---|---|---|---|---|
| Communication Burden | High (to center) | Continuous | Periodic / Continuous | Low (Event-based) |
| Single Point of Failure | Yes | No | No | No |
| Requires Average SoC | No | Often Yes | Yes (by estimation) | No |
| Explicit Overcharge/Discharge Prevention | Possible | Not inherent | Not inherent | Yes (via \(x_0\)) |
| Theoretical Zeno-behavior Guarantee | N/A | N/A | N/A | Yes |
The core strength of our approach lies in the combination of the virtual leader and the event-triggering mechanism. The virtual leader \(x_0\) provides a direct and safe reference for the entire battery energy storage system, explicitly enforcing charge/discharge limits. The event-triggering mechanism drastically reduces the number of communications required for consensus. Batteries only share their state when the local error, measured against the collective network state, exceeds a designed threshold. This is particularly suitable for battery energy storage systems where SoC changes slowly, and continuous updates are redundant.
The mathematical framework, culminating in Theorems 1 and 2, provides solid guarantees. Stability and convergence are ensured under a mild connectivity assumption (Assumption 1), and the proof of a positive minimum inter-event time makes the strategy practical for digital implementation. The control law (2) is distributed, scalable, and robust to the heterogeneity of battery parameters \(m_i\).
Conclusion
This article has presented a comprehensive solution for achieving State-of-Charge balance in a distributed battery energy storage system within a microgrid. The proposed strategy synergistically combines a virtual leader-based tracking objective with an event-triggered communication protocol. The virtual leader ensures all battery units converge to a predefined safe SoC level (e.g., 100% or 20%), effectively mitigating risks associated with overcharge and over-discharge. Simultaneously, the event-triggering mechanism significantly alleviates the communication burden by allowing batteries to update their shared information only when necessary, as defined by a rigorous stability condition.
Key theoretical contributions include proving asymptotic consensus convergence under the proposed protocol and rigorously establishing a positive lower bound for inter-event times, thereby excluding Zeno behavior. Numerical simulations for both charging and discharging operational modes of the battery energy storage system have confirmed the effectiveness, efficiency, and practicality of the method. The approach is fully distributed, enhances system resilience, and contributes to the prolonged lifespan and reliable operation of large-scale battery energy storage systems, facilitating the broader integration of renewable energy sources.
