As the global energy landscape undergoes a profound transformation driven by the urgent need to combat climate change, the integration of high-penetration renewable energy sources has become a cornerstone of sustainable development. From my perspective, the rapid deployment of wind and solar power, while essential for decarbonization, introduces significant instability into power grids due to their intermittent nature. In this context, the battery energy storage system emerges as a critical technological enabler, offering the flexibility and reliability required to balance supply and demand in real-time. This article delves into the planning and configuration of battery energy storage systems within modern power systems, exploring the multifaceted challenges and proposing innovative solutions through market mechanisms and regulatory frameworks. I will analyze the current state, highlight key barriers, and outline pathways for scaling up battery energy storage system deployments, supported by quantitative analyses, tables, and formulas to elucidate complex concepts.
The transition to a renewable-dominated power system is accelerating globally. For instance, in many regions, renewable energy accounted for over 80% of new power capacity additions in recent years, with solar and wind leading the charge. This shift, however, exacerbates grid management issues such as frequency fluctuations, voltage deviations, and peak shaving difficulties. The battery energy storage system addresses these challenges by providing rapid response services, often within milliseconds, thereby enhancing grid stability. To understand its pivotal role, consider the following table summarizing the key functions of a battery energy storage system in power grids:
| Function | Description | Typical Response Time |
|---|---|---|
| Frequency Regulation | Provides primary and secondary frequency control to maintain grid stability. | < 1 second |
| Peak Shaving | Charges during off-peak hours and discharges during peak hours to reduce demand spikes. | Minutes to hours |
| Renewable Integration | Smooths output fluctuations from wind and solar plants, improving power quality. | Seconds to minutes |
| Backup Power | Supplies critical loads during grid outages, enabling islanded operation. | Instantaneous |
| Voltage Support | Injects or absorbs reactive power to regulate voltage levels. | Milliseconds |
Despite these advantages, the widespread adoption of battery energy storage systems faces substantial hurdles. From an economic standpoint, the high upfront capital costs remain a deterrent. The total lifecycle cost of a battery energy storage system can be expressed as:
$$ C_{total} = C_{investment} + \sum_{t=1}^{T} \frac{C_{operation,t} + C_{maintenance,t}}{(1+r)^t} – \frac{S}{(1+r)^T} $$
where \( C_{investment} \) is the initial investment cost, \( C_{operation,t} \) and \( C_{maintenance,t} \) are annual operation and maintenance costs in year \( t \), \( r \) is the discount rate, \( T \) is the system lifetime, and \( S \) is the salvage value. Current models often lack accurate parameters for degradation and recycling, complicating cost-benefit assessments. Moreover, market barriers persist; the battery energy storage system is frequently not recognized as an independent market entity, limiting its revenue streams. The table below illustrates typical cost components for a lithium-ion battery energy storage system:
| Cost Component | Percentage Range | Notes |
|---|---|---|
| Battery Cells | 50-70% | Dominant cost, subject to material price volatility. |
| Power Conversion System (PCS) | 10-15% | Includes inverters and controllers. |
| Balance of System (BOS) | 15-25% | Encompasses wiring, enclosures, cooling, etc. |
| Installation & Commissioning | 5-10% | Labor and grid connection fees. |
| Software & Controls | 3-7% | For monitoring, optimization, and grid integration. |
Technically, the battery energy storage system must overcome issues related to safety, cycle life, and end-of-life management. Thermal runaway risks in batteries necessitate robust safety protocols. The cycle life of a battery energy storage system is often modeled using empirical degradation formulas, such as:
$$ Q_{loss} = A \cdot e^{\left(-\frac{E_a}{RT}\right)} \cdot (C-rate)^z \cdot t^{0.5} $$
where \( Q_{loss} \) is capacity loss, \( A \) is a pre-exponential factor, \( E_a \) is activation energy, \( R \) is the gas constant, \( T \) is temperature, \( C-rate \) is charge/discharge rate, \( z \) is a power factor, and \( t \) is time. This complexity underscores the need for standardized testing and certification.
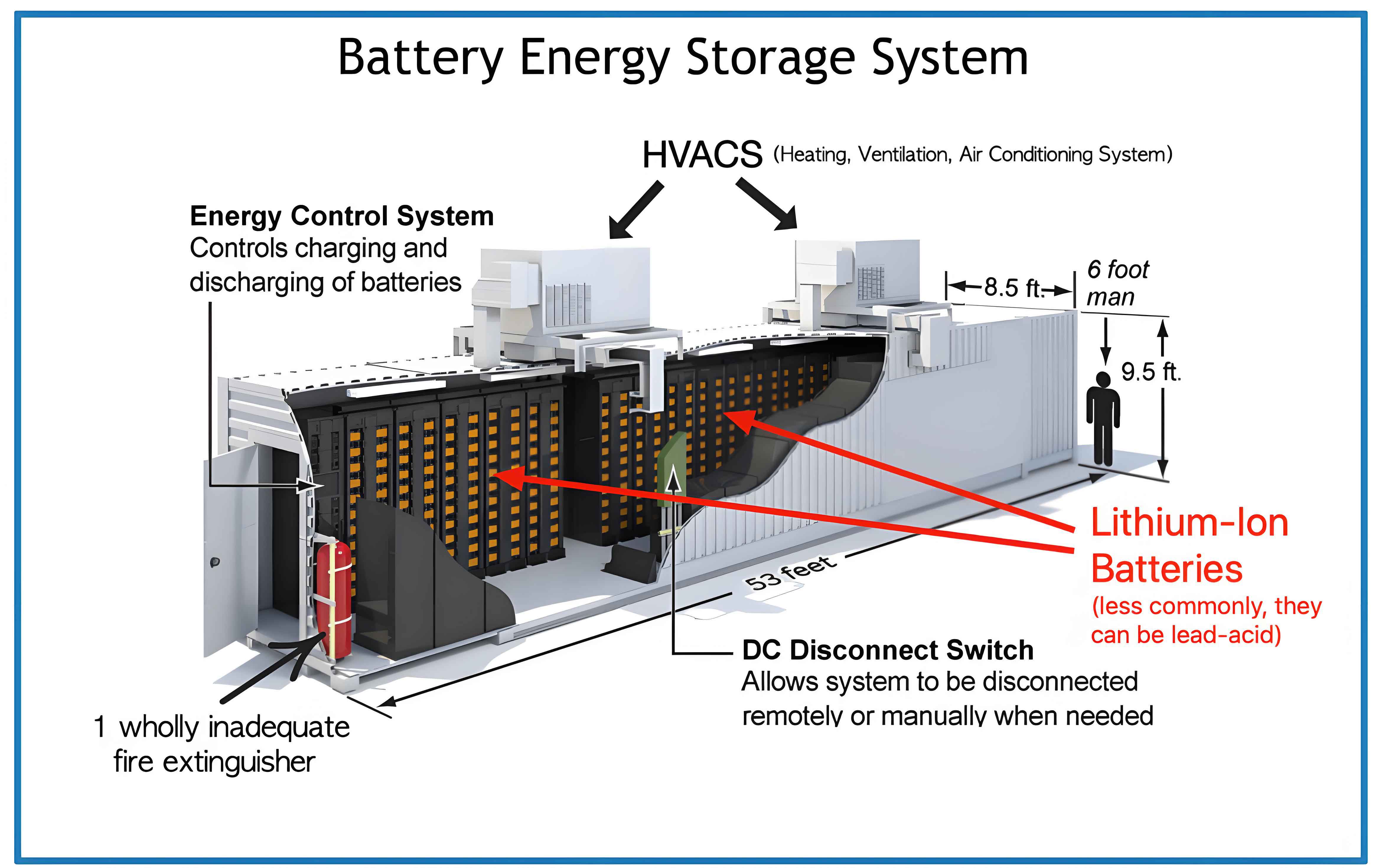
In terms of planning and configuration, optimizing the size and location of a battery energy storage system is crucial for maximizing grid benefits. A common approach involves solving an optimization problem that minimizes total system cost while meeting technical constraints. For example, the objective function for siting a battery energy storage system might be:
$$ \min \sum_{i=1}^{N} \left( C_{inv,i} \cdot x_i + \sum_{t=1}^{T} C_{op,i,t} \cdot y_{i,t} \right) $$
subject to:
$$ P_{min} \leq P_{i,t} \leq P_{max} $$
$$ SOC_{min} \leq SOC_{i,t} \leq SOC_{max} $$
$$ \sum_{i} P_{i,t} = D_t – G_t $$
where \( x_i \) is a binary decision variable for installation at node \( i \), \( y_{i,t} \) is the power output, \( P_{i,t} \) is power, \( SOC_{i,t} \) is state of charge, \( D_t \) is demand, and \( G_t \) is renewable generation. Such models help determine the optimal capacity of a battery energy storage system to alleviate grid congestion and enhance reliability.
The strategic value of a battery energy storage system extends beyond mere cost savings. It facilitates higher renewable penetration by acting as a buffer. For instance, the smoothing effect on solar PV output can be quantified using a low-pass filter representation:
$$ P_{smoothed}(t) = \alpha \cdot P_{PV}(t) + (1-\alpha) \cdot P_{smoothed}(t-1) $$
where \( \alpha \) is a smoothing factor dependent on battery energy storage system response characteristics. This reduces ramp rates and minimizes grid stress. Additionally, the battery energy storage system provides essential ancillary services. In frequency regulation markets, the performance score \( S_{reg} \) for a battery energy storage system can be defined as:
$$ S_{reg} = \frac{\sum |\Delta f_{actual} – \Delta f_{target}|}{\sum |\Delta f_{target}|} \times 100\% $$
where \( \Delta f \) is frequency deviation. A lower score indicates better performance, justifying higher compensation in pay-for-performance markets.
However, the current market design often fails to capture the full value of a battery energy storage system. To address this, I propose a multi-layered market mechanism. First, energy markets should incorporate shorter trading intervals—such as 5-minute or 15-minute blocks—to leverage the fast response of a battery energy storage system. The revenue from energy arbitrage can be estimated as:
$$ R_{arb} = \sum_{t} ( \lambda_{discharge,t} \cdot P_{discharge,t} – \lambda_{charge,t} \cdot P_{charge,t} ) $$
where \( \lambda \) are time-varying prices. Second, ancillary service markets must expand to include products like fast frequency response, spinning reserve, and black start. The compensation for frequency regulation could follow:
$$ C_{reg} = P_{cap} \cdot ( k_1 \cdot S_{speed} + k_2 \cdot S_{accuracy} ) \cdot \lambda_{reg} $$
with \( k_1, k_2 \) as weights for speed and accuracy metrics. Third, capacity markets should recognize the battery energy storage system as a reliability resource. A capacity value \( V_{cap} \) can be derived using effective load carrying capability (ELCC):
$$ V_{cap} = \frac{\Delta LOLP}{\Delta P_{storage}} \cdot \lambda_{capacity} $$
where \( LOLP \) is loss of load probability. The table below compares potential revenue streams for a battery energy storage system in different market structures:
| Market Type | Revenue Source | Key Determinants | Typical Revenue Range ($/kW-year) |
|---|---|---|---|
| Energy Arbitrage | Price differential between peak and off-peak hours. | Price volatility, cycle efficiency. | 50-200 |
| Frequency Regulation | Payments for fast response to frequency deviations. | Performance scores, market clearing prices. | 100-300 |
| Capacity Payments | Compensation for being available during peak demand. | System reliability contributions, auction results. | 80-150 |
| Renewable Integration | Fees for smoothing and firming renewable output. | Contract terms, renewable curtailment rates. | 30-100 |
| Grid Deferral | Savings from delaying transmission/distribution upgrades. | Congestion costs, asset life extension. | 20-80 |
On the regulatory front, policymakers must establish a coherent framework to support battery energy storage system deployment. This includes setting technical standards for safety, interoperability, and recycling. For example, a standard for cycle life testing might specify a minimum number of cycles \( N_{cycle} \) under defined conditions:
$$ N_{cycle} \geq \frac{E_{throughput}}{C_{rated} \cdot DOD} $$
where \( E_{throughput} \) is total energy throughput, \( C_{rated} \) is rated capacity, and \( DOD \) is depth of discharge. Furthermore, regulatory sandboxes can encourage innovation in business models like shared storage or virtual power plants. In a shared battery energy storage system model, the cost allocation among users can be optimized using Shapley value or proportional sharing mechanisms.
Another critical aspect is the integration of a battery energy storage system with artificial intelligence (AI) for advanced control. AI algorithms can predict renewable generation and load patterns, optimizing charge/discharge schedules. A neural network model for state-of-charge (SOC) estimation might take the form:
$$ \hat{SOC}(t+1) = f(W \cdot [I(t), V(t), T(t)] + b) $$
where \( f \) is an activation function, \( W \) and \( b \) are weights and biases, and \( I, V, T \) are current, voltage, and temperature measurements. This enhances the efficiency and longevity of the battery energy storage system.
Looking ahead, the scalability of battery energy storage systems hinges on continued cost reductions and policy support. Projections indicate that global installed capacity could grow exponentially, reaching hundreds of gigawatts by 2030. The levelized cost of storage (LCOS) is a key metric for competitiveness:
$$ LCOS = \frac{C_{total}}{\sum_{t=1}^{T} \frac{E_{discharge,t}}{(1+r)^t}} $$
where \( E_{discharge,t} \) is annual discharged energy. Innovations in battery chemistry, such as solid-state or flow batteries, may further lower LCOS. Additionally, cross-sector coupling—integrating battery energy storage systems with electric vehicles or hydrogen production—can unlock synergies.
In conclusion, the battery energy storage system is indispensable for building resilient, low-carbon power grids. Its planning and configuration require a holistic approach that balances technical, economic, and regulatory dimensions. Through tailored market designs and robust regulatory frameworks, we can unlock the full potential of battery energy storage systems. As I see it, the future grid will rely heavily on these systems to ensure stability amid renewable variability, making them a cornerstone of the energy transition. The journey ahead demands collaboration among stakeholders to refine standards, incentivize investment, and foster innovation, ultimately paving the way for a sustainable energy future dominated by clean, reliable power.
