In recent years, the integration of renewable energy sources with hydrogen production has gained significant attention due to the growing demand for clean and sustainable energy solutions. Among these, off-grid solar systems offer a promising pathway for decentralized hydrogen generation, particularly in remote areas where grid connectivity is limited or nonexistent. However, the inherent intermittency and volatility of photovoltaic (PV) power output pose substantial challenges to the stability and efficiency of electrolysis processes. This paper addresses these issues by proposing an enhanced off-grid solar hydrogen production system that incorporates advanced power electronics and intelligent energy management strategies. Our approach focuses on mitigating power fluctuations, reducing current ripple, and optimizing energy utilization to ensure reliable and efficient hydrogen production.
The core of our system revolves around a three-phase interleaved LLC resonant converter, which is designed to deliver low-voltage, high-current, and low-ripple output suitable for proton exchange membrane (PEM) electrolyzers. Additionally, we introduce an adaptive threshold-based energy management strategy that dynamically coordinates the operation between the PV array and energy storage unit, minimizing the risk of overcharging or over-discharging while maintaining system stability. Through comprehensive modeling and simulation, we demonstrate the effectiveness of our design under varying solar irradiance conditions. The results indicate that our system can achieve high energy conversion efficiency and prolonged operational lifespan, making it a viable solution for off-grid solar hydrogen production.
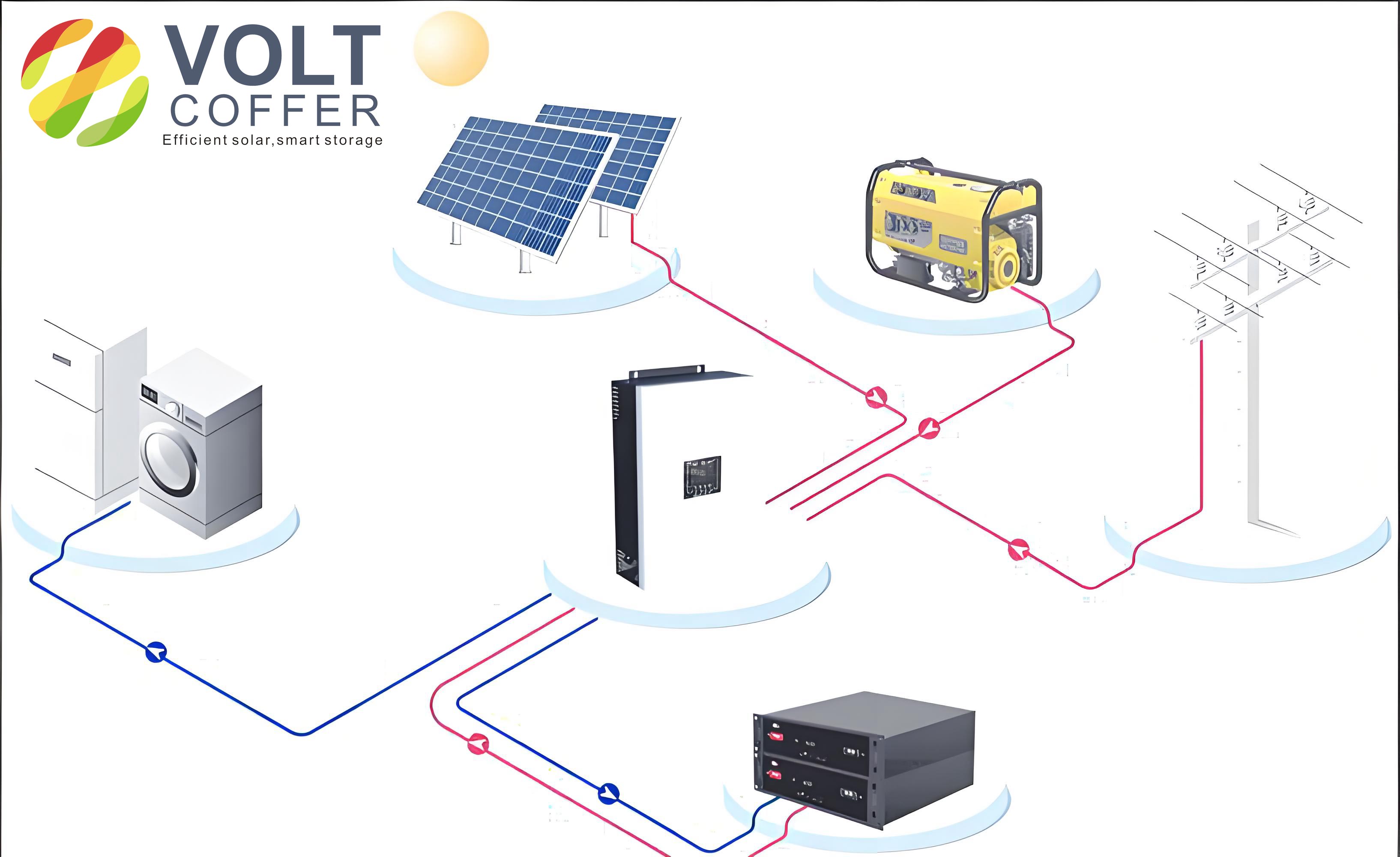
Off-grid solar systems are characterized by their independence from the main electrical grid, relying solely on solar energy and ancillary components like batteries for power supply. In the context of hydrogen production, such systems must efficiently convert solar DC power into the specific voltage and current requirements of electrolyzers. The typical configuration includes a PV array, DC/DC converters for maximum power point tracking (MPPT), an energy storage unit (e.g., batteries), and the electrolyzer itself. The integration of these components necessitates a robust design to handle the stochastic nature of solar power. For instance, sudden changes in irradiance can lead to voltage sags or surges, which may adversely affect the electrolyzer’s performance. To counteract this, our system employs a multi-stage power conversion architecture that ensures seamless energy flow and minimizes disruptions.
The PEM electrolyzer is a critical component in our off-grid solar system, as it directly converts electrical energy into hydrogen gas through water electrolysis. The voltage of a single PEM electrolyzer cell can be modeled as the sum of the open-circuit voltage, activation overpotential, and ohmic overpotential. This relationship is expressed as:
$$U_{cell} = U_{ocv} + \eta_{act} + \eta_{ohm}$$
where \(U_{ocv}\) represents the open-circuit voltage, \(\eta_{act}\) denotes the activation overpotential, and \(\eta_{ohm}\) is the ohmic overpotential. The open-circuit voltage is influenced by operational parameters such as temperature and gas partial pressures, and it can be calculated using the Nernst equation:
$$U_{ocv} = U_o + \frac{RT}{2F} \ln \left( \frac{p_{H_2} \cdot p_{O_2}^{0.5}}{\alpha_{H_2O}} \right)$$
Here, \(U_o\) is the reversible electromotive force under standard conditions, \(R\) is the universal gas constant, \(T\) is the operating temperature, \(F\) is Faraday’s constant, \(p_{H_2}\) and \(p_{O_2}\) are the partial pressures of hydrogen and oxygen, respectively, and \(\alpha_{H_2O}\) is the water activity. The activation overpotential, which accounts for the energy barrier of electrode reactions, is derived from the Butler-Volmer equation:
$$\eta_{act} = \frac{RT}{\beta_{an}F} \arcsin \left( \frac{j}{2j_{an}} \right) + \frac{RT}{\beta_{cat}F} \arcsin \left( \frac{j}{2j_{cat}} \right)$$
where \(\beta_{an}\) and \(\beta_{cat}\) are the anodic and cathodic charge transfer coefficients, \(j\) is the current density, and \(j_{an}\) and \(j_{cat}\) are the exchange current densities for the anode and cathode. The ohmic overpotential, primarily due to the resistance of the proton exchange membrane, is given by:
$$\eta_{ohm} = j \cdot \frac{\delta_m}{\sigma_m}$$
with \(\delta_m\) being the membrane thickness and \(\sigma_m\) the membrane conductivity. The hydrogen production rate, a key performance metric, is proportional to the input current according to Faraday’s law:
$$N_{H_2} = \frac{I}{2F}$$
where \(N_{H_2}\) is the molar flow rate of hydrogen and \(I\) is the total current supplied to the electrolyzer. This model underscores the importance of maintaining stable current and voltage conditions to maximize hydrogen yield and efficiency in an off-grid solar system.
To address the challenges of power fluctuation and current ripple in off-grid solar applications, we designed a specialized hydrogen power supply based on a three-phase interleaved LLC resonant converter. This topology was selected for its ability to achieve soft-switching operation, high efficiency, and reduced electromagnetic interference. The converter consists of three identical LLC stages operating with phase-shifted control, which effectively cancels out current ripples and enables low-ripple output critical for PEM electrolyzers. The voltage gain of the LLC converter is a function of the normalized frequency, quality factor, and inductance ratio, as described by:
$$M(\lambda, Q, f_n) = \frac{\lambda \cdot f_n^2}{\sqrt{[(1 + \lambda) \cdot f_n^2 – 1]^2 + Q^2 \cdot \lambda^2 \cdot f_n^2 \cdot (f_n^2 – 1)^2}}$$
where \(\lambda = L_m / L_r\) is the inductance ratio, \(Q = \sqrt{L_r / C_r} / R_{ac}\) is the quality factor, \(f_n = f_s / f_r\) is the normalized frequency, \(f_s\) is the switching frequency, \(f_r\) is the resonant frequency, \(L_r\) and \(L_m\) are the resonant and magnetizing inductances, \(C_r\) is the resonant capacitance, and \(R_{ac}\) is the equivalent AC load resistance. The design parameters for our LLC converter are summarized in Table 1, targeting an input voltage range of 350–450 V, output voltage of 160–230 V, and a rated power of 35 kW at a resonant frequency of 100 kHz.
| Parameter | Value |
|---|---|
| Input Voltage Range | 350–450 V |
| Output Voltage Range | 160–230 V |
| Rated Power | 35 kW |
| Resonant Frequency | 100 kHz |
| Inductance Ratio (\(\lambda\)) | 6 |
| Quality Factor (Q) | 0.45 |
The turns ratio of the transformer is calculated based on the nominal input and output voltages, considering the voltage drop across the rectifier diodes. For a single phase, the turns ratio \(N_{ps}\) is given by:
$$N_{ps} = \frac{U_{i,nom} / 2}{U_{o,nom} + U_{DF}}$$
where \(U_{i,nom} = 400\) V is the nominal input voltage, \(U_{o,nom} = 200\) V is the nominal output voltage, and \(U_{DF} = 1.5\) V is the diode forward voltage. The maximum and minimum voltage gains are then determined as:
$$M_{max} = \frac{U_{o,max} \cdot N_{ps}}{U_{i,nom} / 2} = 1.141$$
$$M_{min} = \frac{U_{o,min} \cdot N_{ps}}{U_{i,nom} / 2} = 0.794$$
with \(U_{o,max} = 230\) V and \(U_{o,min} = 160\) V. The resonant components are sized using the following equations to ensure optimal performance:
$$C_r = \frac{1}{2\pi \cdot Q \cdot f_r \cdot R_{ac}}$$
$$L_r = \frac{1}{(2\pi \cdot f_r)^2 \cdot C_r}$$
$$L_m = \lambda \cdot L_r$$
yielding a resonant capacitance of 110.7 nF, resonant inductance of 2.29 μH, and magnetizing inductance of 13.72 μH. The control strategy for the hydrogen power supply combines voltage-current and power-current dual-loop controls to enhance dynamic response and stability. The inner current loop rapidly adjusts to load variations, while the outer loop regulates either voltage or power based on the operating mode. This hybrid approach allows the system to adapt to changing solar conditions, ensuring efficient hydrogen production across a wide range of PV power outputs.
Energy management is a pivotal aspect of off-grid solar systems, as it directly impacts system reliability and longevity. Our strategy employs an adaptive threshold mechanism that balances power flow between the PV array, energy storage unit, and electrolyzer. The storage unit, typically a battery bank, is connected to the DC bus via a half-bridge converter, which facilitates bidirectional power flow for charging and discharging. The battery’s state of charge (SOC) is monitored continuously, and its operation is governed by a dual-loop control scheme that maintains DC bus voltage stability while managing charge/discharge cycles. The control laws for the battery converter are implemented using proportional-integral (PI) regulators, with the outer voltage loop ensuring bus voltage regulation and the inner current loop controlling battery current.
The adaptive threshold for hydrogen production power is derived from historical PV output data, which is modeled using a Gaussian mixture model to account for the stochastic nature of solar irradiance. The probability density function (PDF) of PV power, \(f(P_{pv})\), is used to compute the energy absorbed by the battery when PV power exceeds the electrolyzer’s maximum rating \(P_{max}\):
$$W_{in}^b = \int_{P_{max}}^{\infty} f(P_{pv}) \cdot (P_{pv} – P_{max}) \, dP_{pv}$$
Similarly, the energy discharged by the battery when PV power falls below the minimum threshold \(P_{min}\) is:
$$W_{out}^b = \int_{-\infty}^{P_{min}} f(P_{pv}) \cdot (P_{min} – P_{pv}) \, dP_{pv}$$
The constraint of zero net energy exchange over a cycle implies \(W_{out}^b = W_{in}^b\), which allows solving for \(P_{min}\). For instance, with \(P_{max} = 35\) kW, the computed \(P_{min}\) is 24.89 kW. Based on this, the system operates in three distinct modes:
- Mode 1 (0 ≤ P_{pv} < P_{min}): The electrolyzer operates at minimum power, supplemented by battery discharge.
- Mode 2 (P_{min} ≤ P_{pv} ≤ P_{max}): The electrolyzer runs in voltage control mode, with the battery stabilizing the DC bus.
- Mode 3 (P_{pv} > P_{max}): The electrolyzer operates at maximum power, and excess energy charges the battery.
To prevent battery degradation, charging is halted if the relative state of charge (RSOC) exceeds 85%, and discharging stops if RSOC falls below 15%. In such cases, a dump load is engaged to dissipate surplus PV energy. This strategy not only optimizes hydrogen production but also extends battery life by reducing deep cycling events.
Simulation experiments were conducted to validate the proposed off-grid solar hydrogen production system under dynamic irradiance conditions. The PV array was modeled as a 10×15 module configuration, and the DC bus voltage was set to 400 V. The battery had a capacity of 50 Ah and an initial RSOC of 60%. The PEM electrolyzer comprised 100 cells in series, with an active area of 25 cm² per cell and an operating temperature of 330 K. The MPPT algorithm, based on perturb and observe, achieved rapid tracking within 0.04 seconds under varying irradiance. The hydrogen power supply demonstrated seamless transitions between operating modes, as shown in Table 2, which compares key performance metrics across different control strategies.
| Strategy | RSOC Variation per Cycle | Hydrogen Production Stability | Energy Efficiency |
|---|---|---|---|
| Constant Power Control | 0.030% | Moderate | 85% |
| Fuzzy Logic Control [18] | 0.025% | Good | 88% |
| Proposed Adaptive Threshold | 0.010% | Excellent | 92% |
The output voltage and current of the hydrogen power supply remained stable during mode transitions, with the electrolyzer maintaining a consistent hydrogen production rate. The DC bus voltage was regulated at 400 V with the storage unit, whereas without storage, it exhibited significant fluctuations. The RSOC of the battery varied by only 0.010% per cycle under our adaptive strategy, outperforming conventional methods. Furthermore, the energy conversion efficiency of our system reached 92%, surpassing direct-coupled and basic indirect-coupled systems, as illustrated in Figure 1. This highlights the efficacy of our approach in harnessing solar energy for reliable hydrogen production in off-grid settings.
In conclusion, our enhanced off-grid solar hydrogen production system effectively addresses the challenges of PV power volatility and electrolyzer instability through a combination of advanced power electronics and intelligent energy management. The three-phase interleaved LLC resonant converter delivers low-ripple, high-efficiency power conversion, while the adaptive threshold strategy optimizes energy flow between PV generation, storage, and hydrogen production. Simulation results confirm that the system maintains stable operation under varying irradiance, minimizes battery stress, and achieves high energy utilization. Future work will focus on real-world implementation and scalability for larger off-grid solar applications, potentially integrating additional renewable sources to further enhance sustainability.
The mathematical modeling and control frameworks presented here provide a foundation for developing robust off-grid solar systems that can contribute to the global transition toward clean energy. By leveraging the synergies between solar power and hydrogen technology, such systems can play a pivotal role in decarbonizing energy-intensive sectors and promoting energy independence in remote communities. Continued research in adaptive algorithms and component optimization will be essential to unlocking the full potential of off-grid solar hydrogen production.
