The 14th Five Year Plan is a critical and window period for carbon peaking. We need to build a clean, low-carbon, safe and efficient energy system, control the total amount of fossil energy, focus on improving utilization efficiency, implement renewable energy substitution actions, deepen power system reform, and build a new type of power system with new energy as the main body. However, due to the volatility and randomness of renewable energy output, its high proportion of grid connected operation undoubtedly brings new challenges to the economic dispatch of the power system. The large-scale integration of energy storage batteries is an important trend for future development in order to suppress fluctuations in renewable energy and maintain the economic, safe, and stable operation of the power system. As a key operating parameter for energy storage, energy storage life directly affects the efficiency of large-scale energy storage in power systems. Therefore, research on energy storage life has received widespread attention.
In order to address the challenges brought by large-scale grid connection of renewable energy, the joint operation mode of renewable energy and energy storage has become a major measure. At present, more research has been conducted on the economic scheduling problem of multi energy systems including energy storage. Economic dispatch refers to the control of the output of each unit in the system, optimization of system operation, and rational utilization of energy and equipment to achieve the lowest operating cost and ensure the economic operation of the power system, while ensuring the quality of electricity and system safety. Energy storage mainly plays a role in peak shaving and valley filling, serving as backup energy, and suppressing fluctuations in renewable energy, providing important support for the economic, safe, and stable operation of the power system. It can be seen that energy storage plays an increasingly important role in the economic dispatch of power systems. However, there is currently a lack of relevant research on the correlation analysis between energy storage life and economic dispatch results.
Due to the numerous factors and complex mechanisms that affect the decay of energy storage battery life, accurate estimation of energy storage battery life has always been an urgent problem to be solved in the industry. With the gradual increase of energy storage capacity in new power systems, the impact of energy storage life on new power systems cannot be ignored. However, in traditional power system modeling methods for grid side energy storage life, there is a lack of comprehensive consideration of the factors that affect the decay of energy storage life: literature characterizes the cost of energy storage life decay as a quadratic polynomial of energy storage charging and discharging power; Characterize the cost of energy storage life decay as an expression proportional to the amount of energy storage charge and discharge; Convert the maximum number of cycles corresponding to different charging and discharging depths to the condition of full charge and discharge, and perform a cumulative sum to calculate the energy storage life. In summary, the modeling of energy storage life in traditional power systems is relatively simple, and most of them represent energy storage life as a linear function of a measurable electrical quantity, without fully considering the factors that affect the attenuation of energy storage life, resulting in low estimation accuracy.
To obtain accurate estimates of energy storage life, domestic and foreign research teams have proposed various methods, including direct measurement algorithms, model-based methods, and data-driven methods. The direct measurement method is an offline measurement of battery capacity in a laboratory environment. Although this method has high measurement accuracy, the calculation cost is high and can only be carried out in a laboratory environment; The model-based approach is to analyze the decay mechanism of energy storage batteries and construct a life decay model. Although this method has clear physical significance, due to the complexity of the life decay mechanism, it is difficult to directly incorporate complex and variable operating conditions into the decay model through mechanism analysis; The data-driven method, on the other hand, does not require analysis of the energy storage attenuation mechanism and is easy to comprehensively consider the complex and variable operating conditions of energy storage. Therefore, it has received widespread attention. The data-driven method mainly analyzes the historical operating data of energy storage batteries to construct a nonlinear mapping relationship between measurable feature quantities and battery life. Currently, there have been many studies on this method, mainly focusing on models such as Gaussian process regression, support vector regression, and neural networks. The key to this method is to determine appropriate input features to comprehensively reflect the life decay characteristics of energy storage batteries as much as possible. How to determine data that can reflect the battery life characteristics as input to the energy storage life estimation model while ensuring reasonable input dimensions remains a problem that needs further research.
In response to the above issues, this article proposes an economic dispatch method for power systems that accurately considers the lifespan of large-scale energy storage batteries. Firstly, to analyze the significant impact of energy storage life on economic dispatch results, a correlation analysis method between economic dispatch results and energy storage life is proposed based on multi-parameter programming theory, and the analytical relationship between economic dispatch results and energy storage life is derived through theoretical derivation. Furthermore, to ensure the accuracy of economic dispatch results, a deep neural network-based energy storage life estimation method is proposed to achieve accurate estimation of energy storage life. On this basis, a power system economic dispatch method that accurately takes into account the lifespan of large-scale energy storage batteries is proposed, and the effectiveness and practicality of the proposed method are verified based on IEEE-30, IEEE-118 node systems, as well as actual power systems in a certain province in China. The main contributions of this article are as follows:
1) Based on the theory of multi-parameter programming, a correlation analysis method between economic scheduling results and energy storage life is proposed. Firstly, considering constraints such as power balance, a power system economic dispatch model was constructed with the total operating cost of the system as the objective function. Furthermore, taking the lifespan of energy storage batteries as the planning parameter, using multi-parameter programming theory, the economic scheduling results are represented as segmented analytical functions of the planning parameters. Finally, based on this analytical function, the impact of energy storage life on scheduling results is analyzed, and the importance of energy storage life in economic scheduling of power systems with large-scale energy storage is demonstrated.
2) Propose an economic dispatch method for power systems that accurately considers the lifespan of large-scale energy storage batteries. Firstly, a data feature extraction method considering the complex operating conditions of energy storage is proposed to extract features from energy storage charging data fragments. Subsequently, a deep neural network-based energy storage life estimation method was proposed to derive an energy storage life estimation model. Furthermore, using this estimation model to estimate the current energy storage life and embedding accurate energy storage life values into the economic dispatch model proposed in this paper, a power system economic dispatch model considering the life of large-scale energy storage batteries is established. Finally, accurate economic dispatch results are obtained by solving, achieving safe and economic operation of the power system.
1.Economic dispatch model for power systems considering the lifespan of large-scale energy storage batteries
This section considers the characteristics of large-scale grid connected operation of new energy in the new power system and embeds constraints related to energy storage life, constructing an economic dispatch model of the power system that takes into account the lifespan of large-scale energy storage batteries. On this basis, a model transformation method based on optimality equivalence was proposed to solve the economic dispatch model using multi-parameter programming theory, achieving linear transformation of the economic dispatch model.
1.1 Economic dispatch model of power system
This article adopts the commonly used DC power flow model in the industry to model the economic dispatch problem, and on this basis, considers the characteristics of the increase in energy storage installed capacity due to large-scale new energy grid operation. This section takes the total operating cost of the system as the objective function, considers constraints such as power balance and the upper and lower limits of the state of charge of energy storage batteries, and establishes the following economic dispatch model for power systems that takes into account the lifespan of large-scale energy storage batteries.
① Objective function:
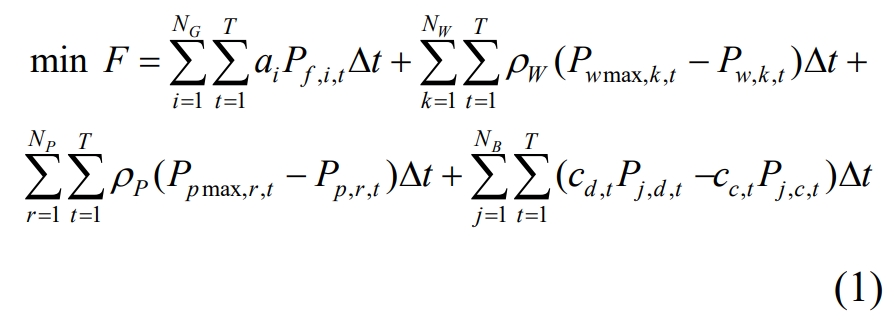
In the formula, F represents the total operating cost of the system; The first item is the operating cost of traditional units, such as thermal power, hydropower units, etc; The second item is the penalty fee for wind abandonment; The third item is the penalty fee for abandoning light; The fourth item is the operating cost of energy storage; AI is the quotation for the i-th traditional unit; ρ W ρ P represents the penalty cost per unit of abandoned air volume and the penalty cost per unit of abandoned light volume; Cc, t, cd, t are the energy storage charging and discharging quotes for time period t respectively; Pf, i, t are the power of the i-th traditional unit in time period t; Pwmax, k, t, Pw, k, t are the maximum and actual power generated by the k-th wind farm during the t period, respectively; Ppmax, r, t, Pp, r, t are the maximum and actual power of the r-th photovoltaic power station during the t period, respectively; Pj, c, t, Pj, d, t are the charging and discharging powers of the jth energy storage during the t period, respectively; NG, NW, NP, and NB represent the number of traditional units, wind farms, photovoltaic power stations, and energy storage power stations, respectively; Δ T is the interval between time periods, and T is the total number of time periods.
② Constraints:
1) Power balance constraints
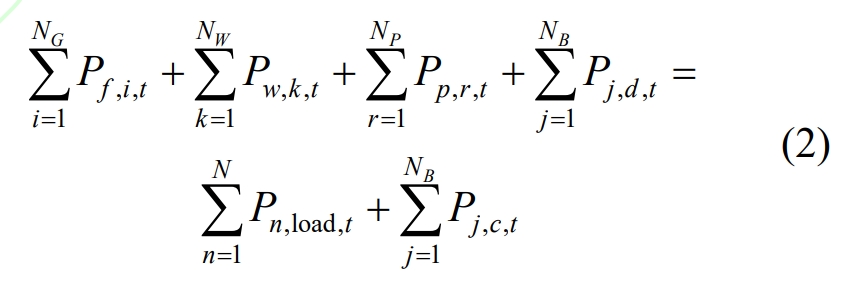
In the formula: t=1,2,…, T; N is the number of nodes connected to the load; Pn, load, t are the loads of the nth node in time period t.
2) Branch power constraint
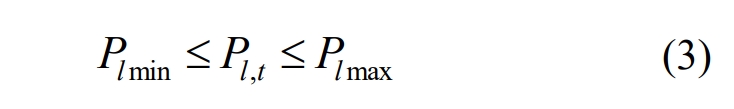
In the formula: t=1,2,…, T; L=1,2,…, L; L is the total number of branches included in the system; Pl, t is the power of the l th branch in time period t; Plmax and Plmin are the upper and lower limits of the power of the l th branch, respectively.
3) Climbing constraints
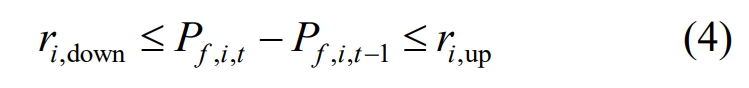
In the formula: t=1,2,…, T; I=1,2,…, NG; Ri, up, ri, and down are the upper and lower limits for traditional unit climbing.
4) Wind power and photovoltaic power constraints
The actual power of wind power and photovoltaic power cannot be higher than the maximum power that can be generated by the wind farm and photovoltaic power station at the current moment, namely:
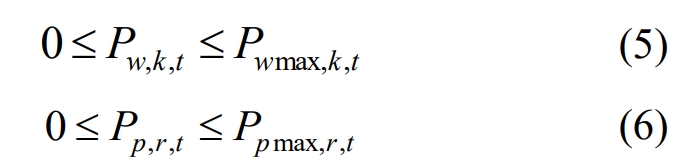
In the formula: t=1,2,…, T; K=1,2,…, NW; R=1,2,…, NP.
5) Constraints related to energy storage operation
The energy storage operation process has the following characteristics: the charging and discharging power cannot exceed the rated power value of the energy storage, namely equations (7) and (8); At the same time period, it can only be in one of the charging, discharging, or resting states, i.e. equation (9); The energy stored in the current period is determined by the energy stored in the previous period, the charging and discharging power of the current period, and the charging and discharging efficiency, i.e. equation (10); There are upper and lower limits for energy storage that can store energy, as shown in equation (11).
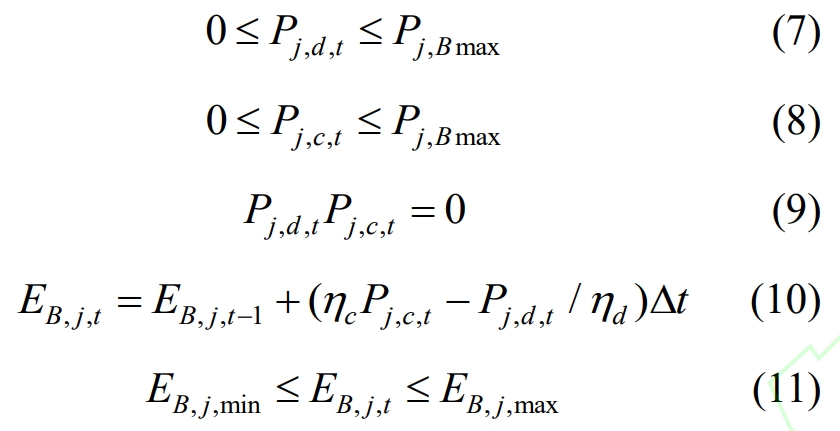
In the formula: t=1,2,…, T; J=1,2,…, NB; Pj, Bmax is the rated power value of the jth energy storage; EB, j, t, EB, j, t-1 are the energy stored in the jth energy storage during time t and t-1 respectively; η C η D represents the charging and discharging efficiency of energy storage; EB, j, max, EB, j, min are the upper and lower limits of the jth stored energy. In addition, for the nonlinear constraint equation (9), when the energy storage is in the charging state, Pj, d, t=0; When the energy storage is in a discharge state, Pj, c, t=0; When the energy storage is in a static state, Pj, d, t and Pj, c, t are all 0.
6) Constraints related to energy storage life
Due to the large scale of energy storage installed in the new power system and the direct impact of energy storage life on the maximum energy storage capacity EB, j, max of energy storage equipment, there is a significant impact on the optimal operation of the power system. Therefore, in order to ensure the accuracy of economic scheduling and the safe use of energy storage, this article proposes constraints related to energy storage life and embeds them into the economic scheduling model, which can be expressed as:
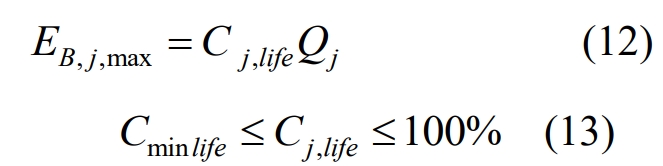
In the formula: j=1,2,…, NB; Cj, life is the life value of the jth energy storage; Qj is the rated capacity of the jth energy storage; Cminlife is the lower limit value of energy storage life. According to equation (12), when the energy storage life Cj and life change, the upper limit EB, j, and max of the energy storage equipment can also linearly change. It is easy to know that the energy storage life directly affects the maximum efficiency that the energy storage equipment can play in the power system; According to equation (13),
In this article, the energy storage life is expressed as a percentage, with Cj, life=100% indicating no decay in the current energy storage life. In addition, when the energy storage life is below a certain value, the energy storage equipment will have a safety hazard and need to be replaced. Therefore, the lower limit value of energy storage life, Cminlife, is set to provide assurance for the safe and stable operation of the energy storage battery.
Equations (1) – (13) represent the economic dispatch model of the power system that takes into account the lifespan of large-scale energy storage batteries. Due to the complex chemical changes that occur inside the energy storage battery during its use, resulting in a decrease in the energy storage life value Cj and life. Therefore, if Cj and life are considered as planning parameters, the above optimization problems (1) – (13) constitute a typical multi-parameter planning problem. However, multi-parameter programming can only be used to solve linear models, and in the aforementioned models, there are nonlinear constraints (9) that cannot be directly solved. If the nonlinear constraint (9) is removed, then (1) – (8) and (10) – (13) are linear models that can be solved using multi-parameter programming.
1.2 Model Transformation Method Based on Optimality Equivalence
To solve the problem of the existence of nonlinear constraints (9) in models (1) – (13) mentioned in section 1.1, which makes it impossible to solve using multi-parameter programming, this section proposes the following inference: when the nonlinear constraints (9) are removed, the optimal solutions of optimization problems (1) – (8) and (10) – (13) always satisfy that Pj, c, t, Pj, d, t are not greater than 0, and the nonlinear constraints (9) are valid, that is, the nonlinear models (1) – (13) are equivalent to linear models (1) – (8) and (10) – (13). The proof is as follows:
For ease of proof, the equality constraints (2), (10), and (12) in optimization problems (1) – (8) and (10) – (13) are transformed into two complementary inequality constraints. For example, the equality constraint (12) can be transformed into two complementary inequality constraints: EB, j, max ≥ Cj, lifeQj and EB, j, max ≤ Cj, lifeQj. After transformation, if the constraints in the model are all inequality constraints, the transformed optimization problem can be recorded as follows:
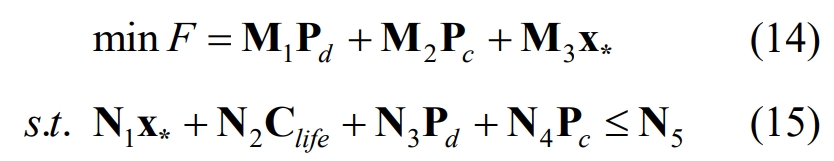
Using the method of proof to the contrary, it is proven that nonlinear models (1) – (13) are equivalent to linear models (1) – (8) and (10) – (13). Assuming that optimization problems (14) and (15) have optimal solutions (x * *, Clife *, Pd *, Pc *), where Pd *>0 and Pc *>0, that is, the nonlinear constraint (9) does not hold. A set of feasible solutions (x * ^, Clife ^, Pd ^, Pc ^) that meet the following conditions can be found:
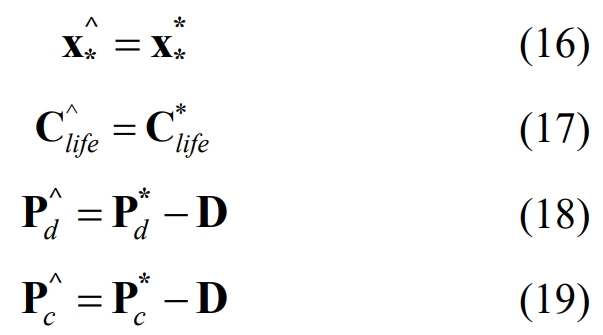
In the equation, D is the coefficient vector. By subtracting the objective functions F * and F ^ of optimization problems (14) and (15) corresponding to the optimal solution (x * *, Clife *, Pd *, Pc *) and feasible solution (x * ^, Clife ^, Pd ^, Pc ^), we can obtain:
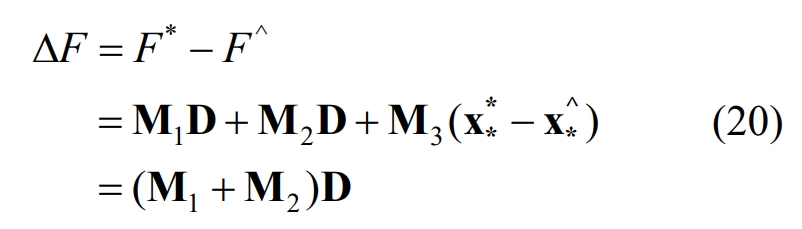
From equations (1) and (14), it can be seen that M1+M2 is the coefficient vector obtained by the difference between the energy storage discharge quotation cd, t and the energy storage charging quotation cc, t. Typically, energy storage is discharged during peak load periods with higher electricity prices and charged during low load periods with lower electricity prices, i.e. cd, t is greater than cc, t, so M1 Å M2>0, Δ The positive or negative of F depends on the positive or negative of D. The specific discussion is as follows:
① D>0:
Yi Zhi Δ F> 0, that is, under the assumed conditions, there exists a feasible solution whose objective function value F ^ (D>0) is less than the objective function value F * of the optimal solution, which contradicts the optimality of the optimization problem. Therefore, the assumption does not hold, and Pd and Pc cannot both be greater than 0. The nonlinear constraint (9) holds.
② D<0:
Yi Zhi Δ F<0, that is, when D<0, the feasible solution does not have optimality, and the objective function value F * of the optimal solution is less than the objective function F ^ of the feasible solution (D<0). Although the feasible solution does not have optimality when D<0, a feasible solution can always be found when D>0, so that its objective function F ^ (D>0) is less than the objective function value F * of the optimal solution. The specific proof is shown in ①, which contradicts the optimality of the optimization problem. If the assumption is not true, Pd and Pc cannot be greater than 0 at the same time, and the nonlinear constraint (9) holds.
In summary, the nonlinear optimization models (1) – (13) are equivalent to the linear optimization models (1) – (8) and (10) – (13).
2. Analysis method for the correlation between economic dispatch results and energy storage life
From the above analysis, it can be concluded that the economic dispatch model (1) – (13) of the power system considering the lifespan of large-scale energy storage batteries proposed in this article is equivalent to the linear optimization models (1) – (8) and (10) – (13), and can be solved using multi-parameter programming. Therefore, in order to analyze the impact of changes in energy storage life on the economic dispatch of power systems, this section proposes a correlation analysis method between economic dispatch results and energy storage life based on multi-parameter programming theory.
To facilitate derivation, this section rewrites optimization problems (14) and (15) into the following compact form:
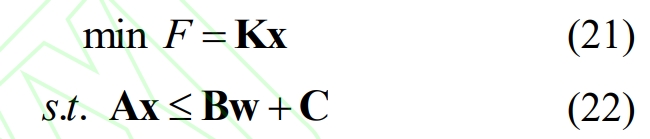
To solve the optimal solutions of optimization problems (21) and (22), construct the Lagrange function L:
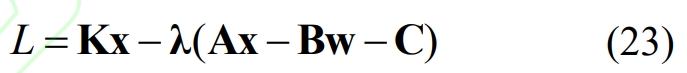
In the equation: λ A vector composed of Lagrange multipliers.
The optimality conditions for optimization problems (21) and (22) include: stagnation point condition (24), complementary relaxation condition (25), original feasibility condition (26), and dual feasibility condition (27).
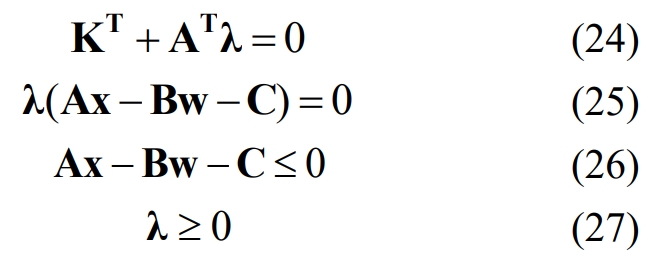
For optimization problems (21) and (22), when the planning parameter w changes within the feasible range of the parameter, there are M sets of effective and ineffective constraint sets. Taking group m as an example, where m=1,2,…, M, the corresponding optimal solution is denoted as xm *, and the optimal value of the objective function is denoted as Fm. From equation (26), it can be concluded that the set of effective and ineffective constraints in the m-th group are equations (28) and (29), respectively:
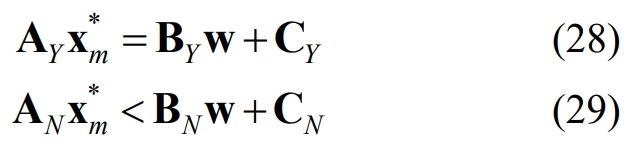
According to equation (28), when AY is a full rank matrix, the optimal solution xm * can be expressed as an analytical function of the planning parameter w, as shown in equation (30); When AY is not a full rank matrix, the Consistent Tie Breaking Rule can be used to ensure the uniqueness of the calculation results [26], thereby obtaining equation (30).
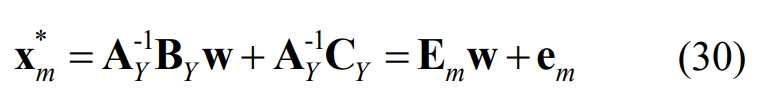
Substituting equation (30) into equation (21), it can be obtained that the optimal value Fm of the objective function can be expressed as an analytical function of the planning parameter w, namely:
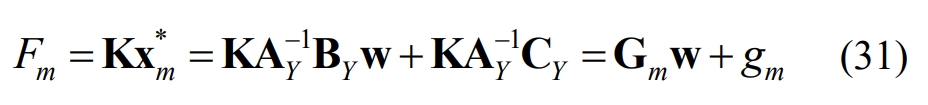
In the formula: Gm is KAY-1BY; Gm is KAY-1CY.
Substituting equation (30) into equation (29) yields equation (32). After shifting and merging similar terms, equation (33) is called the critical domain [27], denoted as CRm, where Aw, m=ANAY ^ -1BY-BN, Bw, m=CN ANAY ^ -1CY.
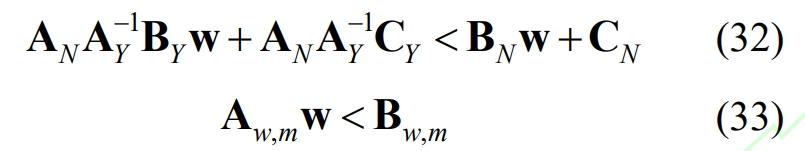
From this, it can be concluded that when w satisfies equation (33), the relationship between xm *, Fm, and w always satisfies equations (30) and (31), that is, when w changes in the critical domain CRm, it always corresponds to a set of effective and ineffective constraint sets.
From the above derivation, it can be inferred that by enumerating the effective and ineffective constraint sets of optimization problems (21) and (22) when the planning parameter w changes within the feasible range of the parameter, M critical domains CRm (m=1,2,…, M) can be obtained. On each critical domain, the optimization variable and objective function are represented by different analytical functions of w. The feasible domain CR of the parameter is the union of all critical domains, that is, CR=CR1 Å CR2 Å… Å CRM, denoted as:
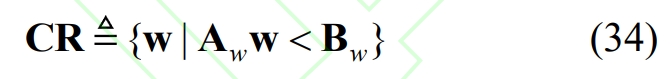
In the formula, Aw and Bw are the coefficient matrices and coefficient vectors obtained by merging the critical domain.
Therefore, on the parameter feasible region CR, the optimization variable x * and the total system operating cost F can be expressed as a piecewise linear function of the planning parameter w, as shown in Figure 1. On the critical domain CRm, xm *=Emw+em, Fm=Gmww+gm, w ∈ CRm, where CRm is the range of variation of parameter w in the piecewise function, m=1,2,…, M, M are the number of piecewise functions.
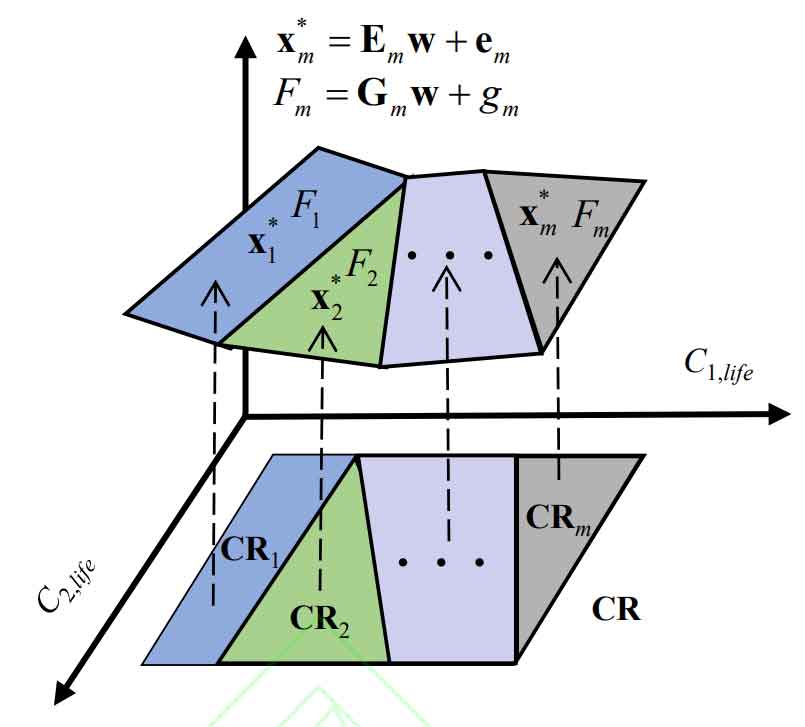
In summary, through the analysis of the correlation between economic dispatch results and energy storage life, it can be concluded that there are M analytical functions for the optimization variable x * and objective function F in the parameter feasible region CR of optimization problems (21) and (22), that is, there is not a single linear relationship between economic dispatch results and energy storage life. This indicates that in power systems containing large-scale energy storage batteries, the value of energy storage life determines its correlation with economic dispatch results and has a direct impact on dispatch results. Therefore, accurate energy storage life values play an important role in the availability of economic dispatch results. Therefore, it is necessary to conduct research on accurate estimation methods for the lifespan of energy storage batteries.
3. Economic dispatch method for power systems that accurately considers the lifespan of large-scale energy storage batteries
According to the analysis in Section 2, accurate energy storage life values play an important role in the availability of economic dispatch results. Therefore, this section proposes an energy storage life estimation method based on deep neural networks, and on this basis, proposes an economic dispatch method for power systems that accurately considers the life of large-scale energy storage batteries.
3.1 Energy Storage Life Estimation Method Based on Deep Neural Networks
Currently, there have been many studies on data-driven methods for estimating the lifespan of energy storage batteries. However, there are still the following issues in existing research: only selecting voltage and current as inputs, lacking consideration of key factors such as temperature and state of charge; Failure to consider the internal connections of each feature data and the possibility of low estimation accuracy due to different data dimensions. To address the above issues, this article proposes a data feature extraction method that considers the complex operating conditions of energy storage. The input data of the life estimation model is feature extracted, and a deep neural network with strong nonlinear fitting ability is selected to build the life estimation model. Furthermore, a deep neural network based energy storage life estimation method is proposed. The estimation principle diagram is shown in Figure 2, and the specific explanation is as follows:
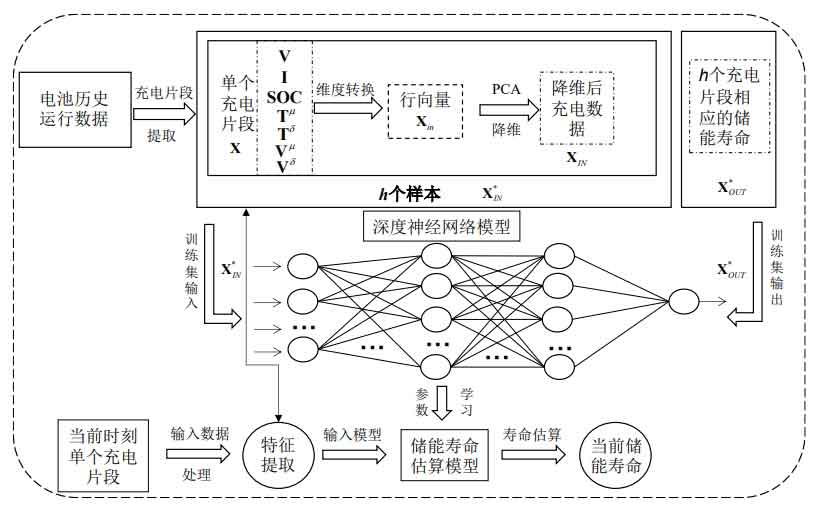
① Data feature extraction:
Due to the advantages of high estimation accuracy and convenient operation when using single charge data of energy storage batteries as input for the life estimation model, this article selects charging data fragments to estimate the life of energy storage batteries. Its main features include total battery voltage (V), total battery current (I), state of charge (SOC), monomer temperature (Tb), and monomer voltage (Vb), where b=1,2,…, B, a total of B monomer batteries. To fully explore the potential relationship between various feature data and complex operating conditions of energy storage, this paper proposes the following data feature extraction method that considers the characteristics of complex operating conditions of energy storage to process the input data.
Firstly, due to the fact that energy storage batteries are composed of single cells of the same model, the differences in Tb and Vb between different single cells are relatively small. Therefore, in this article, the average temperature (T) of each cell is used for Tb and Vb, respectively μ)、 Individual temperature variance (T δ) And the average individual voltage (V μ)、 Individual voltage variance (V δ) Substitute, as shown in equations (35) – (38).
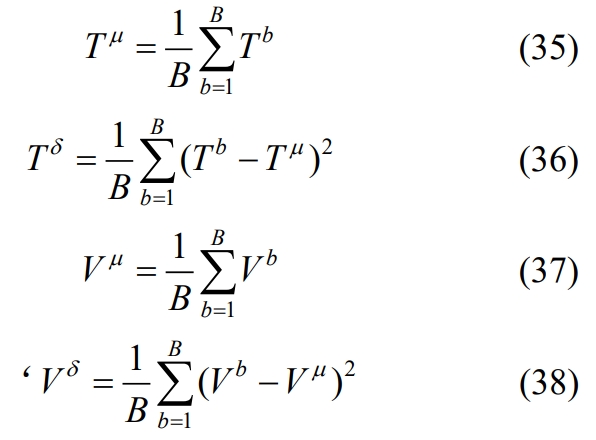
Furthermore, to ensure that the dimensions of the charging data fragments are the same, a systematic sampling method is used to extract R rows from the single charging data to characterize the single charging process, as shown in equation (39), where X represents the sampled charging data. To facilitate model training, the dimension of equation (39) is transformed into a row vector Xin with temporal characteristics, as shown in equation (40).
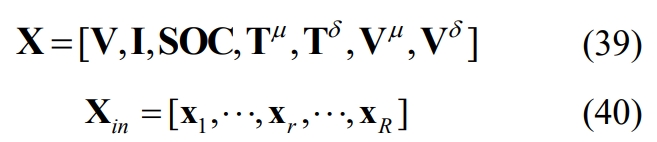
In the formula: V, I, SOC, T μ、 T δ、 V μ、 V δ Is a column vector, such as V=[V1… Vr,…, VR] T, where Vr represents the total voltage of the r th row of charging segment X, r=1,2,…, R; Xr=[Vr, Ir, SOCr, Tr μ, Tr δ, Vr μ, Vr δ]。
Finally, due to the complex attenuation characteristics of energy storage and the large dimensionality of input data, it is difficult to extract key factors for estimating energy storage life. Therefore, in order to reduce the number of data features and fully explore the potential relationships between each feature, this article uses Principal Component Analysis (PCA) to process energy storage data, as shown in Figure 3, which illustrates the dimensionality reduction of energy storage data after PCA processing, The specific processing steps are as follows:
1) Solve the covariance matrix COV of Xin=(Xin) TXin;
2) Solve the eigenvalues and eigenvectors of the covariance matrix COV, and arrange the obtained D eigenvalues in descending order. Take the eigenvectors corresponding to the first d eigenvalues as column vectors to form a matrix P, where d<D;
3) Transform the data Xin into a new space composed of d feature vectors, that is, the dimensionality reduced data XIN=XinP.
At this point, the feature extraction of the input data of the neural network has been completed. The output data of the neural network is the energy storage life value Cj, life under the corresponding charging segment.
② Estimating model construction:
Due to the numerous factors affecting the decay of energy storage life, the estimation model is relatively complex, and deep neural networks have strong learning ability. Therefore, this article selects deep neural networks to build energy storage life estimation models, such as recurrent neural networks, fully connected neural networks, etc.
Furthermore, for the constructed deep neural network model, h charging segments processed by ① are used as inputs to the training set, denoted as XIN *, and the energy storage life values Cj and life under the corresponding charging segments are used as outputs to the training set, denoted as XOUT *. Select optimization algorithms to solve the neural network parameters and obtain an energy storage life estimation model. Finally, extract the charging data fragment at the current time, use the feature extraction method proposed in ① for feature extraction, and input it into the trained model to achieve accurate estimation of the current life value Cj, life, and provide guarantee for the availability of economic scheduling results.
3.2 Economic dispatch method and process for power systems that accurately consider the lifespan of large-scale energy storage batteries
In section 3.1, a data-driven approach was used to accurately estimate the energy storage life Cj and life, providing support for accurate economic scheduling results. On this basis, this section proposes an economic dispatch method for power systems that accurately considers the lifespan of large-scale energy storage batteries, with the following steps:
Step 1: Build an economic dispatch model. Complete the construction of power system economic dispatch models (1) – (8) and (10) – (13) that take into account the lifespan of large-scale energy storage batteries.
Step 2: Estimation of energy storage life. Firstly, use the method proposed in section 3.1 (1) to extract features from h charging data segments in the historical operating data of energy storage. Furthermore, the h charging data segments extracted from the feature extraction are used as inputs to the neural network training set XIN *, and the energy storage life values under the corresponding segments are used as outputs to the training set XOUT *. The energy storage life estimation model is trained using the method proposed in section 3.1 (2). Finally, the charging data fragment at the current time is extracted and input into the energy storage life estimation model to achieve the estimation of Cj and life.
Step 3: Solve the economic dispatch model. Embed the energy storage life values Cj and life obtained in step 2 into equation (12), and use algorithms such as interior point method to solve the models (1) – (8) and (10) – (13) after embedding the energy storage life values Cj and life, and obtain the economic scheduling results.
4. Example analysis
4.1 Example System Description
This article verifies the effectiveness and practicality of the proposed method using IEEE-30 and IEEE-118 node systems, as well as an actual power system in a certain province in China with 661 nodes. One wind farm, one photovoltaic power plant, and two energy storage power plants are all added to the system. Among them, the number of wind farm grid connection nodes is 1, the number of photovoltaic power station grid connection nodes is 2, and the number of energy storage power station grid connection nodes is 3 and 4, respectively. The energy storage operation data is the actual energy storage battery operation data of a domestic company, including characteristics V, I, SOC, Tb, Vb, where b=1,2,…, 20. Time interval Δ T=1, total number of time slots T=24.
Firstly, in Section 4.2, this article represents the total operating cost of the system as a segmented analytical function of energy storage life and verifies the results, demonstrating that energy storage life has a significant impact on economic dispatch results. Secondly, in Section 4.3, this article verifies the accuracy of the proposed economic scheduling method for power systems that accurately considers the lifespan of energy storage batteries by comparing the following economic scheduling methods (M0-M3):
M0: Economic dispatch method for power system, without considering the attenuation of energy storage life, set the energy storage life Cj, life to 1;
M1: Economic dispatch method for power system considering the lifespan of large-scale energy storage batteries, using direct calculation method to calculate the energy storage lifespan Cj, life;
M2: Economic dispatch method for power system considering the lifespan of large-scale energy storage batteries, using a deep neural network-based energy storage lifespan estimation method without extracting data features from charging data;
M3: The economic dispatch method for power systems that accurately considers the lifespan of large-scale energy storage batteries proposed in this article.
Due to the high cost of the direct calculation method used in M1 and its limited applicability in laboratory environments, this method is rarely used in the industry for real-time estimation of energy storage life. However, due to its high estimation accuracy, this section uses the life estimation value obtained by this method as the standard for validity analysis of M2 and M3. Among them, the energy storage life data estimated by the direct calculation method is provided by a domestic company.
All examples in this article were tested in an Intel (R) Core (TM) i7-10750H CPU @ 2.60GHz, 16GB RAM hardware environment. Penalty cost for unit abandoned air volume in the example system ρ W and penalty cost per unit of abandoned light ρ P is 300 yuan and 350 yuan respectively.
| Parameters | Value (30/118/661 node system) |
| Energy storage charging efficiency η C (%) | 90/90/90 |
| Energy storage discharge efficiency η D (%) | 90/90/90 |
| Rated energy storage capacity Qj (MW · h) | 150/800/1500 |
| Rated power of energy storage Pj, Bmax (MW) | 80/500/800 |
| Lower limit of energy storage state of charge EB, j, min (MW · h) | 30/160/300 |
| Lower limit of energy storage life Cminlife | 50%/50%/50% |
The parameter settings for energy storage in each node system are shown in Table 1, and the pricing for energy storage charging and discharging is shown in Table 2. The example uses a fully connected neural network for model building, with 2 hidden layers, 200 neurons per layer, and an initial learning rate of 0.001. The Adam optimizer and mean square error loss function are used.
| Time interval | Energy storage charging quotation cc, t | Energy storage discharge quotation cd, t |
| 07:00-11:00 and 16:00-20:00 | 200 | 300 |
| 11: 00-16:00 and 20:00-23:00 | 150 | 300 |
| 23:00-24:00 and 00:00-07:00 | 100 | 300 |
4.2 Correlation test between economic dispatch results and energy storage life
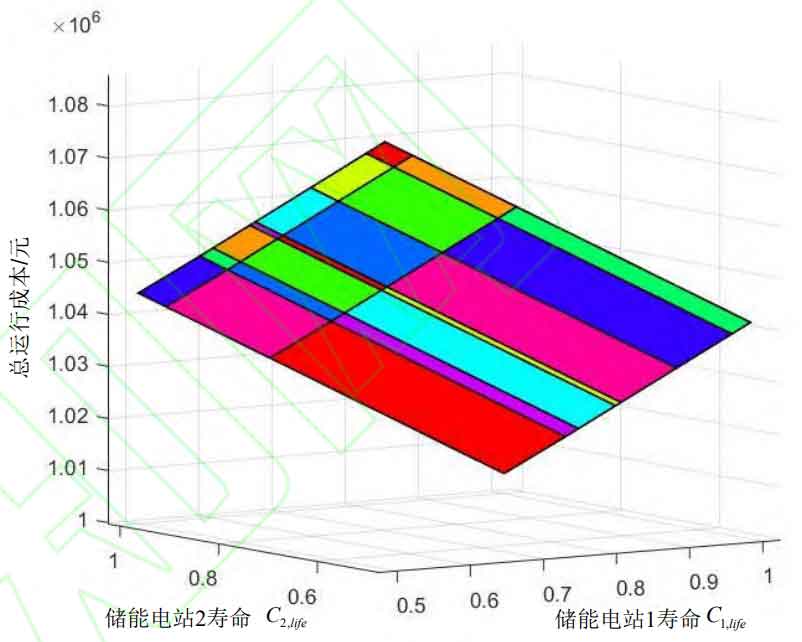
This section verifies the effectiveness of the economic scheduling results and energy storage life correlation analysis method proposed in this paper in an IEEE-30 node system. The planning parameter w=[C1, life; C2, life], and the analytical relationship between the total operating cost of the system and the planning parameters can be obtained from equation (31), as shown in Figure 5. A total of 21 critical domains are characterized, with each color representing a critical domain. Under different critical domains, there are different analytical relationships. For example, in the critical domains CR19 and CR20, the analytical relationship between the total operating cost F of the system and the planning parameter w can be expressed as:
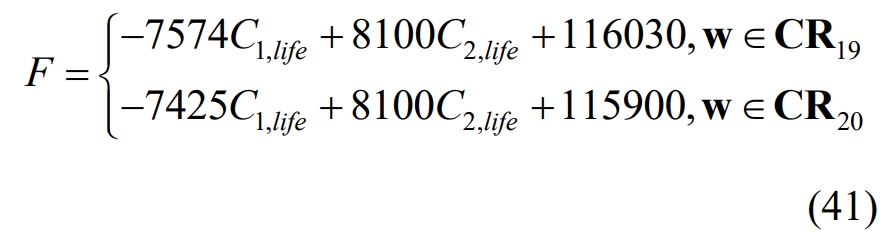
From this, it can be concluded that the total operating cost F of the system is not a single linear relationship with the energy storage life Cj, life. Therefore, modeling the energy storage life Cj, life as a simple linear function can lead to inaccurate estimation of the energy storage life, which in turn affects the availability of economic scheduling results.
| Energy Storage Station 1 Life C1, life | 100% | 80% | 60% | 50% |
| System operating cost/yuan | 100372 | 101992 | 103612 | 104422 |
In addition, as shown in Figure 4, changes in the energy storage life Cj and life will have a direct impact on the total operating cost F of the system, while other input quantities remain unchanged. To demonstrate this conclusion, the following calculation example is set: assuming C2 and life are 100%, with C1 and life taking 100%, 80%, 60%, and the minimum value of 50%, the total operating cost of the system is shown in Table 3. When C1 and life change from 100% to 50%, the total operating cost of the system increases from 100372 yuan to 104422 yuan, an increase of 4050 yuan, with an increase percentage of about 4.03%. It has been demonstrated that changes in energy storage life have a significant impact on economic dispatch results, that is, the attenuation of energy storage life will lead to an increase in the total operating cost of the system.
Through the above analysis, it can be concluded that changes in energy storage life have a significant impact on economic dispatch results. In addition, the operating conditions of energy storage are directly related to the energy storage life, that is, the life of energy storage under different operating conditions will change accordingly, thereby affecting the economic dispatch results. Therefore, in order to demonstrate the changes in energy storage life under different operating conditions, the following calculation example is set: selecting actual energy storage battery operating data and reflecting different energy storage operating conditions by setting different temperatures. Run the energy storage at 25 degrees Celsius and 0 degrees Celsius respectively, and estimate the energy storage life Cj and life using the three energy storage life estimation methods in M1-M3. The results are shown in Table 4. When the temperature changes from 25 degrees Celsius to 0 degrees Celsius, the estimated energy storage life Cj and life of M1-M3 decrease by 15.54%, 13.62%, and 14.77%, respectively. It has been demonstrated that different operating conditions have a significant impact on the energy storage life.
| Plan | M1 | M2 | M3 |
| Energy storage life Cj, life at 25 degrees Celsius | 86.9% | 91.8% | 88.7% |
| 0 ° C energy storage life Cj, life | 73.4% | 79.3% | 75.6% |
In summary, changes in the operating conditions of energy storage will cause changes in the energy storage life Cj and life, and the changes in the energy storage life Cj and life will have a significant impact on the economic dispatch results.
4.3 Verification of the effectiveness of economic dispatch methods for power systems that accurately consider the lifespan of large-scale energy storage batteries
This section uses actual energy storage battery operation data and daily load data to verify the effectiveness of the economic dispatch method proposed in this paper, which accurately considers the lifespan of large-scale energy storage batteries, in the IEEE-118 node system and the actual power system of a certain province in China with 661 nodes.
The three energy storage life estimation methods proposed in M1-M3 were used to estimate the life values of energy storage plant 1 and 2 on a certain day, and the results are shown in Table 5. The three economic dispatch methods proposed in M0-M3 were applied to the IEEE-118 node system and the actual power system of a certain province in China with 661 nodes, respectively. The economic dispatch results are shown in Tables 6 and 7, respectively.
| Plan | M1 | M2 | M3 |
| Energy Storage Station 1 Life C1, life | 87.5% | 92.3% | 88.3% |
| Energy Storage Station 2 Life C2, life | 85.6% | 91.7% | 86.6% |
From Table 5, it can be seen that the relative errors of M2 and M3 compared to the more accurate values M1 for the life estimation results of two energy storage power stations are 5.49%, 0.91%, and 7.13%, 1.17%, respectively. Easy to obtain, data-driven estimation methods for energy storage life have high accuracy. In addition, M3 adopts the data feature extraction method proposed in this article to extract features from the input data of the neural network, fully exploring the potential relationships between various feature data, which greatly improves the estimation accuracy and demonstrates the effectiveness of the energy storage life estimation method proposed in this article.
| Plan | M0 | M1 | M2 | M3 |
| Total operating cost/yuan | 3.25×10^6 | 3.44×10^6 | 3.36×10^6 | 3.43×10^6 |
| Traditional unit cost/yuan | 1.30×10^6 | 1.37×10^6 | 1.34×10^6 | 1.37×10^6 |
| Abandoning Wind Penalty/Yuan | 7.61×10^5 | 7.61×10^5 | 7.61×10^5 | 7.61×10^5 |
| Penalty for Abandoning Light/Yuan | 9.42×10^5 | 1.10×10^6 | 1.04×10^6 | 1.09×10^6 |
| Energy storage operation cost/yuan | 2.48×10^5 | 2.06×10^5 | 2.23×10^5 | 2.09×10^5 |
From Table 6, it can be seen that by analyzing the economic scheduling results of M1, M2, M3, and M0 in the IEEE-118 node system, it can be concluded that the total operating costs of M1, M2, and M3 systems have increased by 190000 yuan, 110000 yuan, and 180000 yuan respectively compared to M0, with growth percentages of about 5.85%, 3.38%, and 5.54%. The reason for this deviation is that the battery will experience life loss during actual operation, while M0 does not consider the decay of energy storage life, This results in a significant deviation between the results obtained from M0 and M1-M3, indicating the necessity of incorporating energy storage life into the economic dispatch model. Although the total operating cost of M0’s system is lower than that of M1-M3, the economic scheduling results of M0 do not take into account the decrease in the maximum energy storage capacity caused by the decay of energy storage life, which may result in the inability to achieve its scheduling results, and unreasonable scheduling plans may lead to certain safety accidents. In addition, by analyzing the results of M2, M3, and M1, it can be concluded that the relative errors between the total operating costs of the M2, M3 systems and the true value M1 are 2.33% and 0.29%, respectively, indicating that the relative errors of the economic scheduling method M3 proposed in this paper are relatively small.
| Plan | M0 | M1 | M2 | M3 |
| Total operating cost/yuan | 8.27×10^6 | 8.81×10^6 | 8.59×10^6 | 8.77×10^6 |
| Traditional unit cost/yuan | 4.15×10^6 | 4.37×10^6 | 4.28×10^6 | 4.35×10^6 |
| Abandoning Wind Penalty/Yuan | 1.94×10^6 | 1.94×10^6 | 1.94×10^6 | 1.94×10^6 |
| Penalty for Abandoning Light/Yuan | 1.96×10^6 | 2.27×10^6 | 2.16×10^6 | 2.27×10^6 |
| Energy storage operation cost/yuan | 2.22×10^5 | 2.00×10^5 | 2.14×10^5 | 2.04×10^5 |
To further demonstrate the applicability of the economic dispatch method M3 proposed in this article, Table 7 shows the economic dispatch results of M0-M3 in the actual power system of a certain province in China. Analysis shows that the total operating costs of M1, M2, and M3 systems have increased by 540000 yuan, 320000 yuan, and 500000 yuan compared to M0, respectively, with growth percentages of about 6.53%, 3.87%, and 6.05%; The relative errors between the total operating cost of M2 and M3 systems and the true value M1 are 2.50% and 0.45%, respectively. From the above analysis, it can be concluded that the results obtained from M3 are relatively close to the true value M1, indicating the effectiveness of the economic scheduling method M3 proposed in this paper.
5.Conclusion
To demonstrate the importance of energy storage life in the economic dispatch of new power systems and incorporate accurate energy storage life values into the economic dispatch model to ensure safe and economic operation of the power system, this paper proposes an analysis method for the correlation between economic dispatch results and energy storage life, as well as a data-driven estimation method for energy storage life. Based on this, a power system economic dispatch method that accurately considers the life of large-scale energy storage batteries is proposed. Finally, the effectiveness of the proposed method was verified through testing examples in IEEE-30, IEEE-118 node systems, and actual power systems in a certain province in China. The main content includes:
1) To demonstrate the importance of energy storage life in new power systems, a segmented analytical function between economic dispatch results and energy storage life was constructed based on multi-parameter programming theory. This indicates that changes in energy storage life can have a significant impact on economic dispatch results, and it is necessary to include it in the economic dispatch model.
2) To ensure the safe and economic operation of the power system, this article proposes a deep neural network-based method for estimating the lifespan of energy storage batteries, and proposes a data feature extraction method that fully explores the potential connections between various features, achieving accurate estimation of energy storage lifespan. On this basis, a power system economic dispatch method that accurately considers the lifespan of large-scale energy storage batteries is proposed, ensuring the availability of economic dispatch results for the new power system.
The research object of this article is the economic scheduling problem of power systems containing large-scale energy storage batteries, which has certain practical significance. In addition, with the development of the energy storage industry, the scale of physical energy storage, electromagnetic energy storage, etc. in the power system is increasing. The analysis of the potential impact of the lifespan of such energy storage on the economic dispatch of the power system is the focus of future research.
