The transition towards sustainable energy systems is fundamentally dependent on the ability to store electrical energy efficiently and reliably. In this context, the battery energy storage system (BESS) has emerged as a cornerstone technology, enabling the integration of intermittent renewable sources like solar and wind into the grid. Among various electrochemical storage technologies, lithium-ion (Li-ion) batteries dominate the landscape of modern battery energy storage system deployments due to their high energy density, long cycle life, and decreasing cost. The safe and reliable operation of these large-scale battery energy storage system installations is paramount, as failures can lead to significant economic losses, grid instability, and serious safety hazards including thermal runaway and fire.
Fault diagnosis, therefore, is a critical function within the Battery Management System (BMS) of any battery energy storage system. Its primary goal is to detect abnormal conditions early, identify the specific fault type, and trigger appropriate mitigation strategies before a minor anomaly escalates into a catastrophic failure. However, accurately diagnosing incipient or “micro-faults” presents a formidable challenge. These early-stage faults, such as subtle overcharging, deep discharging, or the onset of an internal short circuit, often manifest with weak signatures that are easily masked by measurement noise, system disturbances, and the inherent nonlinear, time-varying behavior of the battery itself. Traditional model-based diagnostic methods, which rely on precise mathematical models of the battery energy storage system, struggle with these complexities, leading to poor timeliness and low diagnostic accuracy for micro-faults.
This limitation has catalyzed the exploration of data-driven approaches for battery energy storage system fault diagnosis. By leveraging historical and real-time operational data—current, voltage, and temperature—these methods learn the complex mapping between measurable signals and underlying battery health states without requiring an explicit, first-principles physical model. This article explores and develops an advanced data-driven diagnostic framework tailored for micro-faults in Li-ion-based battery energy storage system. The core of our proposal is a hybrid intelligent model that synergizes the pattern recognition prowess of a Probabilistic Neural Network (PNN) with the global optimization capability of the Sparrow Search Algorithm (SSA).
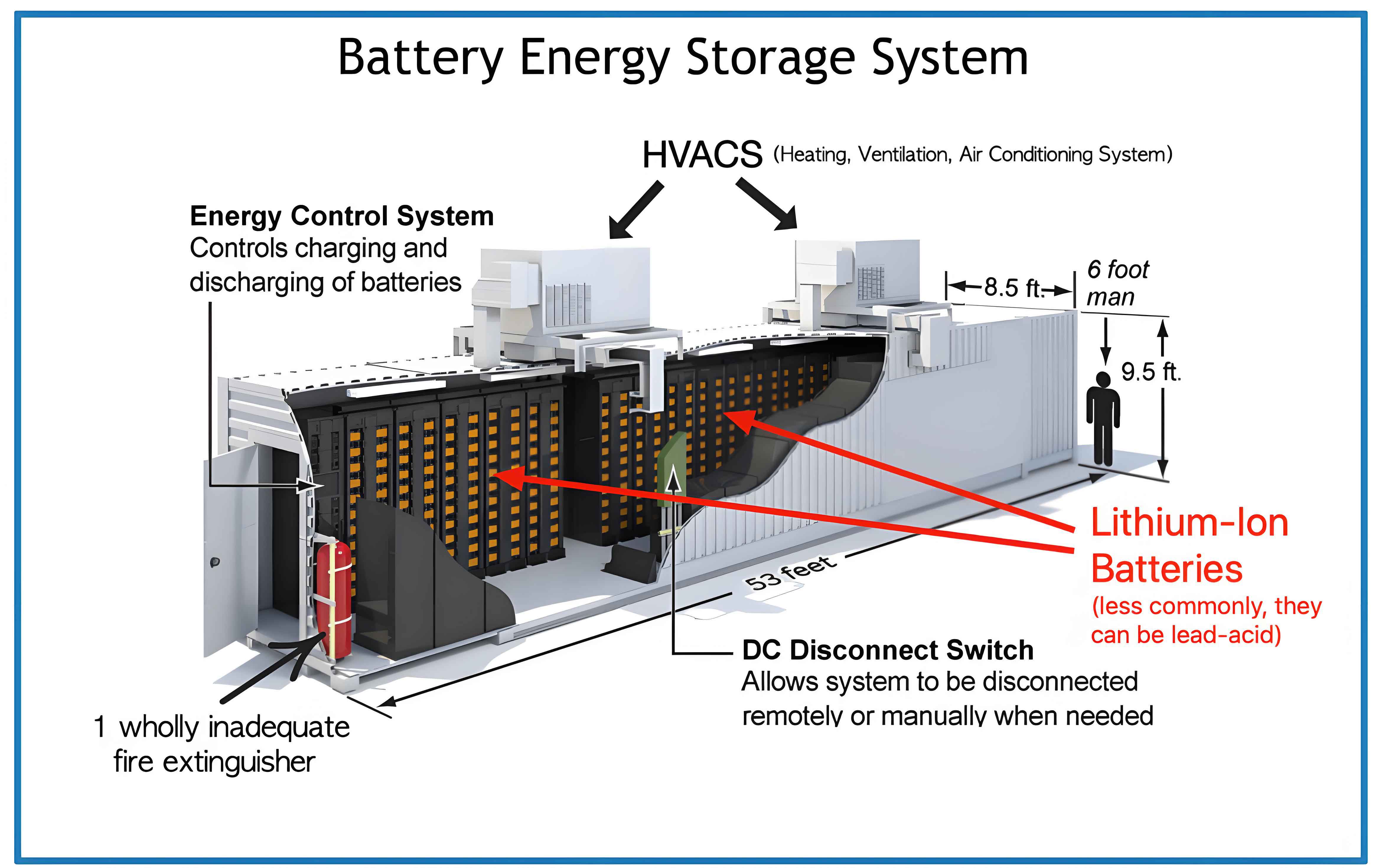
Challenges in Battery Energy Storage System Fault Diagnosis and the Data-Driven Paradigm
Faults in a Li-ion battery energy storage system can be broadly categorized based on their progression: long-term faults (e.g., gradual capacity fade and impedance rise due to aging) and temporary/abusive faults (e.g., overcharge, over-discharge, internal/external short circuit). While long-term degradation is critical for state-of-health estimation, temporary abusive faults often develop rapidly and pose immediate safety risks. Their early “micro-fault” phase is characterized by subtle deviations in operational parameters.
Model-based methods, which use equivalent circuit models or electrochemical models to generate residual signals for fault detection, are limited by model inaccuracy, parameter drift, and computational burden, especially for large-scale battery energy storage system. Signal-processing methods can be sensitive to noise. In contrast, data-driven methods directly learn the diagnostic logic from data, offering superior adaptability to the nonlinear dynamics of the battery energy storage system. Machine learning algorithms, including Support Vector Machines (SVM) and Artificial Neural Networks (ANN), have shown promise. However, challenges remain in achieving high accuracy, ensuring generalization, avoiding local optima during training, and optimizing model hyperparameters automatically.
Our diagnostic framework is designed to address these challenges. It operates through a structured pipeline: 1) Data Acquisition from the battery energy storage system (current $I$, voltage $V$, temperature $T$), 2) Feature Extraction and Labeling (associating data segments with fault classes: Normal, Overcharge, Over-discharge, Short Circuit), 3) Model Training using an optimized PNN, and 4) Online Diagnosis. The innovation lies in using the SSA to optimally configure the PNN, enhancing its diagnostic precision for a battery energy storage system.
Theoretical Foundation: Probabilistic Neural Network and Sparrow Search Algorithm
Probabilistic Neural Network (PNN) for Pattern Recognition
The PNN is a feedforward neural network derived from Bayesian decision theory and non-parametric probability density estimation. It is particularly effective for classification problems, such as fault diagnosis in a battery energy storage system, due to its fast training (a single pass), guaranteed convergence to an optimal Bayesian classifier given sufficient data, and robustness. A standard PNN comprises four layers:
- Input Layer: Distributes the feature vector $\mathbf{x} = [x_1, x_2, …, x_n]^T$ (e.g., processed $V$, $I$, $T$ features) to all neurons in the pattern layer.
- Pattern Layer: Each neuron in this layer corresponds to one training sample from a specific fault class $g$. It computes the similarity between the input $\mathbf{x}$ and its stored pattern using a Gaussian kernel function:
$$ \phi_{gi}(\mathbf{x}) = \frac{1}{(2\pi)^{n/2} \sigma^n} \exp\left( -\frac{||\mathbf{x} – \mathbf{x}_{gi}||^2}{2\sigma^2} \right) $$
where $\mathbf{x}_{gi}$ is the $i$-th training vector from class $g$, $n$ is the feature dimension, and $\sigma$ is the smoothing parameter (or spread). This parameter critically affects performance: a small $\sigma$ leads to overfitting, while a large $\sigma$ causes over-smoothing and loss of detail. - Summation Layer: Neurons in this layer sum the outputs from the pattern layer for each class:
$$ S_g(\mathbf{x}) = \sum_{i=1}^{N_g} \phi_{gi}(\mathbf{x}) $$
where $N_g$ is the number of training samples for class $g$. This sum approximates the class-conditional probability density $f(\mathbf{x}|g)$. - Output Layer: Implements a competitive (winner-takes-all) function, selecting the fault class with the highest posterior probability:
$$ \hat{g} = \arg \max_g \left( S_g(\mathbf{x}) \right) $$
This selected class $\hat{g}$ is the diagnostic output for the battery energy storage system state.
The main challenge in deploying PNN for battery energy storage system diagnosis is the manual and often suboptimal selection of the smoothing parameter $\sigma$.
Sparrow Search Algorithm (SSA) for Hyperparameter Optimization
The SSA is a recent metaheuristic optimization algorithm inspired by the foraging and anti-predation behaviors of sparrow flocks. It is known for strong global search ability and fast convergence. The algorithm population consists of three types of virtual sparrows:
- Discoverers: Individuals with better fitness that guide the search direction.
- Followers: Individuals that follow the discoverers to forage.
- Scouts: A portion of individuals that stay alert to danger and initiate escape behaviors.
The position of each sparrow represents a candidate solution, which in our case is a specific value for the PNN’s $\sigma$. Let the population be represented by matrix $\mathbf{X}$ with $N$ sparrows and $D$ dimensions (here, $D=1$ for $\sigma$):
$$ \mathbf{X} = \begin{bmatrix} x_{1,1} \\ x_{2,1} \\ \vdots \\ x_{N,1} \end{bmatrix} $$
The fitness of each sparrow $F(\mathbf{x}_i)$ is evaluated. For our diagnostic task, the fitness function is defined as the sum of the classification error rates on both the training and validation datasets when the PNN uses that specific $\sigma$. Minimizing this fitness directly optimizes the PNN’s diagnostic accuracy and generalization for the battery energy storage system.
The position update rules are key to SSA’s effectiveness. The discoverer’s position update is governed by:
$$ x_{i,j}^{t+1} = \begin{cases}
x_{i,j}^t \cdot \exp\left( -\frac{i}{\alpha \cdot T_{max}} \right), & \text{if } R_2 < ST \\
x_{i,j}^t + Q \cdot L, & \text{if } R_2 \geq ST
\end{cases} $$
where $t$ is the current iteration, $T_{max}$ is the maximum iteration, $\alpha \in (0,1]$, $R_2 \in [0,1]$ is a random alarm value, $ST \in [0.5, 1.0]$ is a safety threshold, $Q$ is a random number from a normal distribution, and $L$ is a vector of ones. This rule balances exploration and exploitation.
The follower’s position update is:
$$ x_{i,j}^{t+1} = \begin{cases}
Q \cdot \exp\left( \frac{x_{worst}^t – x_{i,j}^t}{i^2} \right), & \text{if } i > N/2 \\
x_{best}^{t+1} + |x_{i,j}^t – x_{best}^{t+1}| \cdot A^+ \cdot L, & \text{otherwise}
\end{cases} $$
where $x_{best}$ and $x_{worst}$ are the current global best and worst positions, and $A$ is a random matrix with elements ±1. Scouts are randomly selected to update their positions to escape local optima if they detect danger. By iteratively applying these update rules, SSA efficiently searches for the optimal $\sigma$ that minimizes the PNN’s diagnostic error, thereby creating an optimized SSA-PNN model for the battery energy storage system.
Experimental Characterization of Battery Energy Storage System Fault Signatures
To train and validate the SSA-PNN model, experimental data capturing both normal and faulty operations of a commercial LiFePO4 (LFP) battery cell—a common chemistry in stationary battery energy storage system—were generated. Key cell parameters are summarized in Table 1.
| Parameter | Specification |
|---|---|
| Nominal Capacity | 280 Ah |
| Nominal Voltage | 3.2 V |
| Standard Energy | 896 Wh |
| Voltage Window | 2.5 V – 3.65 V (T > 0°C) |
| Standard Charge/Discharge Rate | 0.25C |
Three primary abusive conditions were induced to simulate micro-faults relevant to a battery energy storage system:
- Over-discharge: The cell was discharged from a normal state at a constant current of -280 A (approx. -1C) beyond its lower cut-off voltage down to 0 V. The voltage profile showed a sharp drop during the deep over-discharge phase, accompanied by a more pronounced temperature rise compared to normal operation, indicating increased polarization and internal resistance.
- Overcharge: The cell was charged at a constant current beyond its upper voltage limit (3.65 V) until failure at approximately 5.45 V. A voltage plateau around 4.85 V was observed, potentially indicating intensive side reactions, while the cell temperature exhibited a continuous and significant increase, signaling the onset of thermal instability.
- External Short Circuit (ESC): The cell terminals were connected through a low-resistance path. The voltage instantaneously collapsed to near 0 V, while a surge current exceeding 4000 A was observed. The cell temperature rapidly increased, with different sensor locations showing similar rise rates, indicating uniform internal heat generation.
From these tests, a dataset of 1000 samples was constructed, each sample being a time-windowed vector of features extracted from $V$, $I$, and $T$ signals, labeled into one of four classes: Normal (Class 1), Overcharge (Class 2), Over-discharge (Class 3), and Short Circuit (Class 4). This dataset forms the basis for developing the diagnostic model for the battery energy storage system.
Model Implementation, Results, and Comparative Analysis
The dataset was randomly split into a training set (750 samples) and an independent test set (250 samples). The SSA was configured with parameters listed in Table 2 to optimize the PNN’s $\sigma$ parameter.
| Parameter | Value |
|---|---|
| Population Size | 30 |
| Maximum Iterations ($T_{max}$) | 100 |
| Proportion of Discoverers | 20% |
| Proportion of Scouts | 10% |
| Safety Threshold ($ST$) | 0.8 |
| Search Boundary for $\sigma$ | [0.01, 2] |
The SSA successfully navigated the parameter space and converged to an optimal smoothing factor. The trained SSA-PNN model was then evaluated. Its performance on the test set demonstrated exceptional diagnostic capability, achieving a classification accuracy of 100% (250/250 correct) for the distinct fault classes. This indicates the model’s high precision in distinguishing the subtle signature differences between micro-faults in a simulated battery energy storage system cell.
To quantify the advantage offered by the SSA optimization, the diagnostic performance was compared against two baseline models: a standard PNN with an empirically chosen $\sigma$ and a conventional Backpropagation Neural Network (BPNN). The BPNN, a widely used multi-layer perceptron, was trained using the error backpropagation algorithm. The comparative results are summarized in Table 3.
| Diagnostic Method | Key Characteristics | Test Set Accuracy | Remarks |
|---|---|---|---|
| SSA-Optimized PNN (Proposed) | Automatic $\sigma$ optimization via SSA; Bayesian classification foundation. | 100% | Highest accuracy. Fast, one-pass training. Avoids local optima. |
| Standard PNN (Baseline) | Manually selected, fixed $\sigma$ parameter. | ~97% | Performance highly sensitive to the choice of $\sigma$. Suboptimal tuning leads to errors. |
| BPNN (Baseline) | Multi-layer network trained via gradient descent. | ~95% | Prone to getting trapped in local minima during training. Requires longer, iterative training. |
The analysis clearly shows the superiority of the proposed SSA-PNN framework. The standard PNN’s performance is constrained by the difficulty of manually tuning $\sigma$, while the BPNN suffers from convergence issues and longer training times. The SSA-PNN effectively overcomes these limitations, providing a robust, accurate, and efficient diagnostic tool suitable for the demanding environment of a battery energy storage system. The optimization process can be formally expressed as finding the parameter $\sigma^*$ that minimizes the diagnostic loss $\mathcal{L}$:
$$ \sigma^* = \arg \min_{\sigma \in \mathbb{R}^+} \mathcal{L}_{Diagnostic}(\text{PNN}(\sigma); \mathcal{D}_{train}, \mathcal{D}_{val}) $$
where SSA serves as the solver for this optimization problem.
Conclusion and Perspectives
Ensuring the safety of large-scale Li-ion battery energy storage system installations necessitates advanced, reliable fault diagnosis capable of detecting incipient failures. This article presented an intelligent fault diagnosis framework based on a Probabilistic Neural Network optimized by the Sparrow Search Algorithm. The method directly addresses the core challenge of diagnosing micro-faults with weak signatures by leveraging a data-driven paradigm that bypasses the need for precise physical models of the complex battery energy storage system.
The SSA automates the critical task of tuning the PNN’s smoothing parameter, optimizing the model’s ability to generalize from training data and accurately classify unseen fault conditions. Experimental validation on a commercial LFP cell, subjected to overcharge, over-discharge, and short circuit tests, demonstrated the framework’s efficacy. The proposed SSA-PNN model achieved perfect classification on the test set, significantly outperforming both a standard PNN with manual parameter setting and a traditional BPNN. This result underscores the potential of hybrid intelligent systems combining optimized neural networks with metaheuristic algorithms for enhancing the reliability and safety management of battery energy storage system.
Future work will focus on scaling this cell-level diagnostic approach to module- and pack-level battery energy storage system, where fault propagation and coupling between cells introduce additional complexity. Furthermore, investigating online, adaptive learning mechanisms for the SSA-PNN model to accommodate the evolving characteristics of a battery energy storage system throughout its operational lifetime will be crucial for practical, long-term deployment. The integration of this diagnostic layer with proactive fault-tolerant control strategies represents the next frontier in building resilient and safe grid-scale battery energy storage system.
