The accurate prediction of the Remaining Useful Life (RUL) of lithium-ion batteries stands as a cornerstone for ensuring the safety, reliability, and economic viability of Battery Energy Storage Systems (BESS). These systems are pivotal in the modern energy landscape, supporting grid stability, integrating renewable sources, and powering electric vehicles. Battery degradation is an inevitable, complex process influenced by operational stressors such as charge-discharge cycling, temperature fluctuations, and mechanical vibrations. The ability to forecast a battery’s RUL enables proactive maintenance, prevents catastrophic failures, and optimizes the utilization of the entire battery energy storage system, thereby maximizing return on investment. This article presents a comprehensive data-driven framework for RUL prediction, leveraging multi-task learning and an enhanced ensemble algorithm to achieve high accuracy under diverse operational conditions.
The core challenge in RUL prognostics lies in mapping subtle, often non-linear changes in measurable battery parameters to its long-term degradation trajectory. Traditional model-based approaches, which rely on detailed electrochemical or empirical models, can be computationally intensive and difficult to generalize across different battery chemistries and usage profiles. In contrast, data-driven methods directly learn the relationship between extracted features (health indicators) and the remaining lifespan from historical data. Our proposed methodology integrates feature engineering based on battery degradation modes, a multi-task learning strategy for efficient feature utilization, and a robust ensemble learning model for final prediction. The integration of these components is designed to enhance prediction robustness and accuracy specifically for battery energy storage system applications where operational conditions are variable.
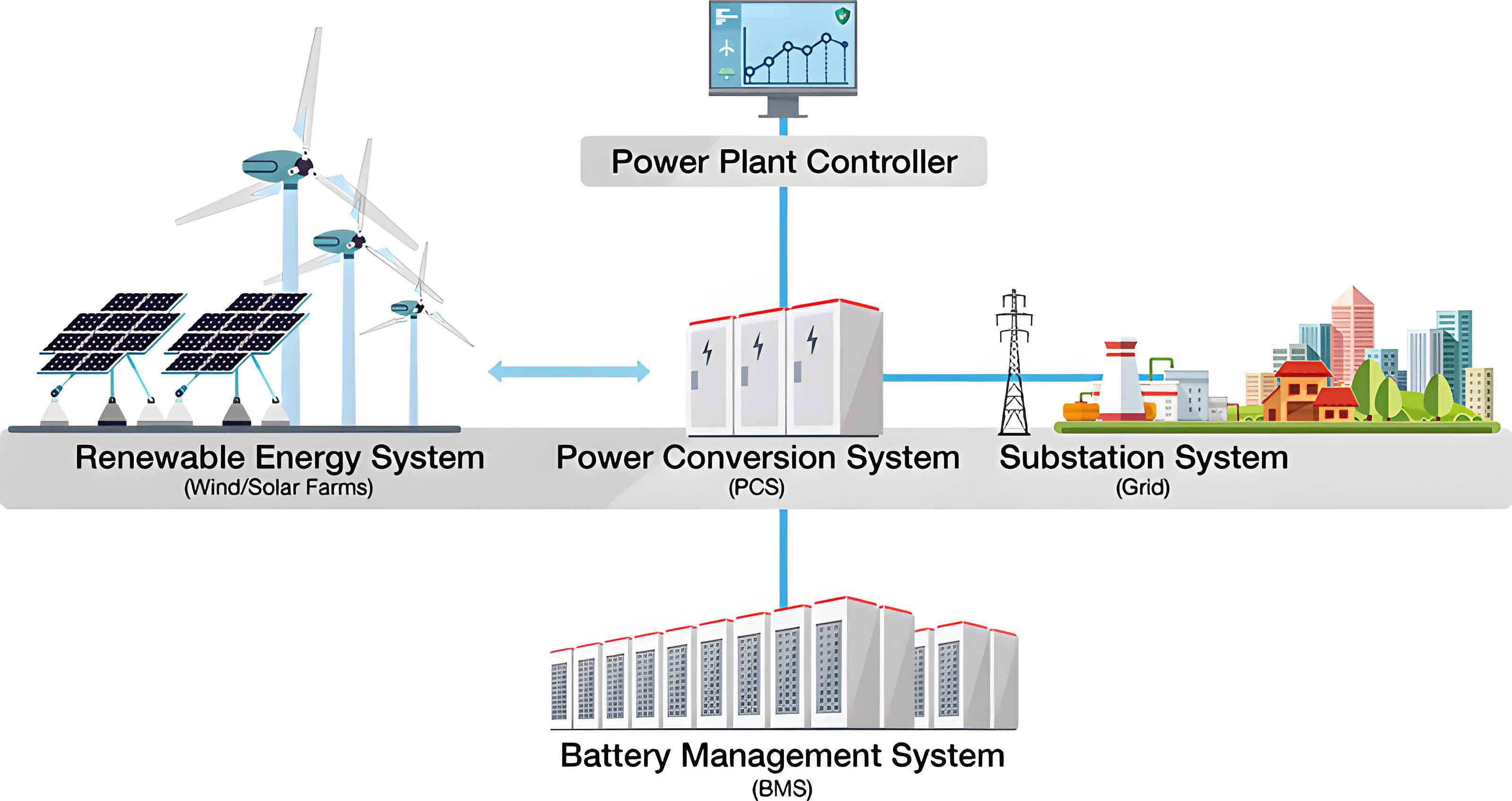
The performance and longevity of a battery energy storage system are directly dictated by the health of its individual cells. RUL prediction is therefore not merely a cell-level diagnostic but a system-level imperative. An inaccurate RUL estimate can lead to either premature replacement, increasing costs, or unexpected system downtime and safety hazards. Our work focuses on creating a predictive model that is both accurate and adaptable, capable of learning from correlated degradation patterns across different stress conditions to improve predictions even when data for a specific condition is limited. This is particularly valuable for managing large-scale battery energy storage system deployments where full lifecycle testing under all possible scenarios is impractical.
Degradation Feature Quantification for Battery Health Assessment
Effective RUL prediction begins with the identification and extraction of meaningful health indicators. We derive features from two primary diagnostic techniques: Incremental Capacity-Differential Voltage (IC-DV) analysis and Electrochemical Impedance Spectroscopy (EIS). These features quantitatively describe the fundamental degradation modes within a lithium-ion battery.
From the IC-DV curves, we quantify three primary loss mechanisms:
1. Loss of Conductivity (LC): Related to increased resistance in the electrodes and electrolyte.
2. Loss of Active Material (LAM): Related to the structural disconnection or dissolution of cathode/anode materials.
3. Loss of Lithium Inventory (LLI): Related to the irreversible consumption of cyclable lithium ions, primarily due to Solid Electrolyte Interphase (SEI) growth and other side reactions.
The quantification formulas at cycle \(i\) are:
$$MLC_i (\%) = \frac{\max(V_0) – \max(V_i)}{\max(V_0)} \times 100$$
$$MLAM_i (\%) = \frac{\max\left(\frac{dQ}{dV_0}\right) – \max\left(\frac{dQ}{dV_i}\right)}{\max\left(\frac{dQ}{dV_0}\right)} \times 100$$
$$MLLI_i (\%) = \frac{\max(Q_0) – \max(Q_i)}{\max(Q_0)} \times 100$$
where \(V_0\), \(Q_0\), and \(dQ/dV_0\) represent the initial voltage, capacity, and IC peak value, respectively. \(V_i\), \(Q_i\), and \(dQ/dV_i\) are the corresponding values at cycle \(i\).
From the EIS spectra, typically modeled by an equivalent circuit, we extract four key impedance parameters that correlate with different physical processes:
1. Ohmic Resistance (\(R_{\Omega}\)): Represents the sum of resistances from electrodes, electrolytes, and contacts.
2. Charge Transfer Resistance (\(R_{ct}\)): Associated with the kinetics of the electrochemical reactions at the electrode interfaces.
3. SEI Layer Resistance (\(R_{SEI}\)): Corresponds to the resistance of the passivation layer on the anode.
4. Warburg Diffusion Impedance (\(Z_w\)): Reflects the resistance related to solid-state lithium-ion diffusion within the electrode particles.
The evolution of these parameters, summarized in the table below, provides a complementary view of the internal state of the battery energy storage system cells.
| Stress Condition | LC (%) Final | LAM (%) Final | LLI (%) Final | \(R_{\Omega}\) Trend | \(R_{ct}\) Trend |
|---|---|---|---|---|---|
| Reference (Static) | 1.63 | 22.08 | 27.87 | Gradual Increase | Significant Increase |
| X-axis Vibration | 1.79 | 28.12 | 32.28 | Gradual Increase | Significant Increase |
| Y-axis Vibration | 1.69 | 30.83 | 31.98 | Gradual Increase | Significant Increase |
| Z-axis Vibration | 1.90 | 36.94 | 35.12 | Gradual Increase | Significant Increase |
Multi-Task Learning Framework for Feature Correlation Exploitation
In a real-world battery energy storage system, batteries may experience a variety of overlapping stress conditions (e.g., different temperature zones, varying charge rates, mechanical vibrations). Collecting sufficient labeled aging data for every possible condition is prohibitively expensive and time-consuming. Multi-Task Learning (MTL) offers an elegant solution by allowing a model to learn multiple related tasks (e.g., RUL prediction under condition A, B, C) simultaneously. The fundamental hypothesis is that sharing representations between related tasks can improve generalization and data efficiency for each individual task.
In our context, the different “tasks” are predicting the RUL under different vibration conditions. While the magnitude of degradation may vary, the underlying physical degradation modes (LC, LAM, LLI) and their manifestations in EIS parameters are often correlated. An MTL architecture can learn a shared feature representation that captures these common degradation patterns. This shared knowledge helps the model make better predictions for a specific condition, especially when the training data for that condition is limited. The learning objective in a hard-parameter sharing MTL setup can be formulated as minimizing a composite loss function:
$$\min_{\theta_{sh}, \theta_1, \ldots, \theta_T} \sum_{t=1}^{T} \lambda_t \cdot L_t(f(X_t; \theta_{sh}, \theta_t), Y_t)$$
where \(T\) is the number of tasks (conditions), \(\theta_{sh}\) represents the parameters of the shared layers, \(\theta_t\) represents the task-specific parameters for task \(t\), \(L_t\) is the loss function for task \(t\), \(X_t\) and \(Y_t\) are the data and labels for task \(t\), and \(\lambda_t\) is a weighting coefficient balancing the contribution of each task. This approach allows the model dedicated to a specific battery energy storage system operating profile to benefit from patterns learned from other, related profiles, leading to more robust and generalizable RUL estimates across the fleet.
Enhanced LightGBM Model with Adaptive Robust Loss
As the core regression model for RUL prediction, we employ Light Gradient Boosting Machine (LightGBM), a highly efficient gradient boosting framework. It offers advantages like lower memory usage and faster training speed compared to other tree-based ensemble methods, which is crucial for potential real-time applications in a battery energy storage system management unit. LightGBM builds an additive model in a forward stage-wise manner:
$$F_T(x) = \sum_{t=1}^{T} f_t(x), \quad f_t \in \mathcal{F}$$
where each \(f_t\) is a weak learner (decision tree) from the tree space \(\mathcal{F}\), and \(T\) is the number of trees. At each stage \(t\), a new tree \(f_t\) is fitted to the negative gradient (pseudo-residuals) of the loss function relative to the current model \(F_{t-1}(x)\).
The key enhancement we propose is the replacement of the standard loss function (e.g., Mean Squared Error) with an Adaptive Robust Loss (AR-Loss) function. Real-world sensor data from a battery energy storage system can contain noise and outliers, which can disproportionately influence the gradient and degrade model performance. The AR-Loss, parameterized by \(\alpha\) and \(c\), provides a continuum of robust loss functions:
$$L_{AR}(x, \alpha, c) = \begin{cases}
0.5(x/c)^2, & \alpha = 2 \\
\log((x/c)^2 + 1), & \alpha = 0 \\
1 – \exp(-0.5(x/c)^2), & \alpha = -\infty \\
\frac{|\alpha-2|}{\alpha} \left( \left(\frac{(x/c)^2}{|\alpha-2|} + 1 \right)^{\alpha/2} – 1 \right), & \text{otherwise}
\end{cases}$$
where \(x\) is the residual (prediction error). By adapting the shape parameter \(\alpha\), the loss function can behave like L2 loss (\(\alpha=2\)), Cauchy loss (\(\alpha=0\)), or a form of Welsch loss (\(\alpha=-\infty\)), effectively limiting the influence of large residuals (outliers). The scale parameter \(c\) controls the transition point between inliers and outliers. This robustness is vital for maintaining prediction stability in the noisy operational environment of a battery energy storage system.
Integrated Prediction Framework and Experimental Validation
The complete RUL prediction framework, which we term the Multi-Task Ensemble Learning (MTEL) model, integrates the components described above. The operational workflow is as follows:
Step 1: Data Preparation & Feature Extraction. Cycle aging data is collected under multiple conditions. For each cycle, the IC-DV curves and EIS spectra are processed to calculate the seven health indicators: MLC, MLAM, MLLI, \(R_{\Omega}\), \(R_{ct}\), \(R_{SEI}\), and \(Z_w\). The target variable, RUL, is defined as the number of remaining cycles until capacity fade reaches a predefined End-of-Life (EOL) threshold, typically 80% of nominal capacity.
Step 2: Multi-Task Data Structuring. The dataset is partitioned by operating condition (task). The feature correlations across tasks are analyzed to configure the MTL strategy (e.g., degree of parameter sharing).
Step 3: Model Architecture & Training. An AR-Loss enhanced LightGBM model is set within an MTL architecture. The model is trained to minimize the composite MTL loss function. Hyperparameters (e.g., number of leaves, learning rate, \(\alpha\) and \(c\) for AR-Loss) are optimized using a search strategy like Tree-structured Parzen Estimator (TPE).
Step 4: RUL Prediction & Evaluation. For a new battery cell under a specific condition, the extracted features are fed into the corresponding task-specific branch of the trained model to obtain the RUL prediction. Performance is evaluated using standard metrics:
– Mean Absolute Error (MAE): \( \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i| \)
– Root Mean Square Error (RMSE): \( \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2} \)
– Mean Absolute Percentage Error (MAPE): \( \text{MAPE} = \frac{100\%}{n} \sum_{i=1}^{n} \left| \frac{y_i – \hat{y}_i}{y_i} \right| \)
To validate the framework, lithium-ion batteries were subjected to aging tests under simulated driving profiles, including different vibration axes (X, Y, Z) and a static reference condition. The discharge profile mimicked real driving with variable C-rates. The proposed MTEL model was compared against several state-of-the-art data-driven models. The results, summarized in the table below, demonstrate the superior accuracy and robustness of our approach for predicting RUL in a battery energy storage system context.
| Prediction Model | Average MAE (%) | Average MAPE (%) | Average RMSE (%) | Key Characteristic |
|---|---|---|---|---|
| Support Vector Regression (SVR) | < 1.80 | < 0.075 | < 2.05 | Kernel-based, sensitive to parameters |
| Extreme Learning Machine (ELM) | < 1.63 | < 0.068 | < 1.85 | Fast training, random hidden layer |
| Gradient Boosting Decision Tree (GBDT) | < 1.36 | < 0.062 | < 1.55 | Sequential tree building |
| eXtreme Gradient Boosting (XGBoost) | < 1.30 | < 0.060 | < 1.48 | Regularized model, precise splitting |
| LightGBM (Baseline) | < 1.23 | < 0.059 | < 1.40 | Efficient histogram-based splitting |
| Proposed MTEL Model (AR-Loss-LightGBM) | < 1.40 | < 0.058 | < 1.20 | Multi-task learning with robust loss |
Conclusion and Implications for Battery Energy Storage Systems
This article has detailed an advanced data-driven framework for predicting the remaining useful life of lithium-ion batteries, with direct applications to the management and maintenance of large-scale battery energy storage system installations. By quantifying fundamental degradation modes from IC-DV analysis and EIS, we established a physically-informed feature set that accurately reflects internal battery health. The incorporation of multi-task learning allows the model to leverage correlated aging patterns across different operational conditions, enhancing prediction accuracy and data efficiency—a critical advantage for systems deployed in diverse environments.
The core innovation lies in the integration of an Adaptive Robust Loss function into the LightGBM ensemble learner. This enhancement significantly improves the model’s resilience to measurement noise and outliers, which are commonplace in field data from operational battery energy storage system sites. Experimental validation under simulated driving conditions with mechanical vibration stress confirmed that the proposed MTEL model achieves state-of-the-art prediction accuracy, as evidenced by lower RMSE, MAE, and MAPE values compared to other benchmark algorithms.
The successful implementation of such a prediction model can transform the operational strategy for a battery energy storage system. It enables a shift from reactive or scheduled maintenance to proactive, condition-based maintenance. System operators can optimize replacement schedules, balance loads across cells of varying health, and provide more accurate performance guarantees. Ultimately, this contributes to lower levelized cost of storage, improved system safety and reliability, and greater confidence in the long-term deployment of battery energy storage system technology as a cornerstone of the future energy grid. Future work will focus on extending the framework to incorporate real-time data streams and adapting it to other critical failure modes within a battery energy storage system.
